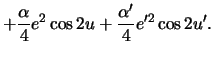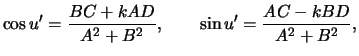Topologiya i metrika par keplerovskih orbit
<< 1. Vvedenie | Oglavlenie | 3. Topologiya par orbit >>
2. Evklidovo rasstoyanie mezhdu dvumya keplerovskimi orbitami
Oboznachim cherez ![]() keplerovskii ellips, rassmatrivaemyi kak
mnozhestvo tochek v
keplerovskii ellips, rassmatrivaemyi kak
mnozhestvo tochek v ![]() . Pust'
. Pust' ![]() - evklidovo
rasstoyanie mezhdu dvumya orbitami, t.e. naimen'shee znachenie rasstoyaniya
- evklidovo
rasstoyanie mezhdu dvumya orbitami, t.e. naimen'shee znachenie rasstoyaniya
![]() mezhdu parami tochek, lezhashih na sootvetstvuyushih ellipsah.
S XIX stoletiya opublikovany sotni rabot, posvyashennyh opredeleniyu
mezhdu parami tochek, lezhashih na sootvetstvuyushih ellipsah.
S XIX stoletiya opublikovany sotni rabot, posvyashennyh opredeleniyu
![]() razlichnymi priblizhennymi sposobami. Al'ternativnyi podhod sostoit
v svedenii zadachi k resheniyu uravneniya
razlichnymi priblizhennymi sposobami. Al'ternativnyi podhod sostoit
v svedenii zadachi k resheniyu uravneniya
My postroili algoritm naimen'shei slozhnosti dlya opredeleniya ![]() .
Imenno, postroili igrayushii rol'
.
Imenno, postroili igrayushii rol' ![]() trigonometricheskii mnogochlen
vos'moi stepeni
trigonometricheskii mnogochlen
vos'moi stepeni ![]() ot ekscentricheskoi anomalii
ot ekscentricheskoi anomalii ![]() . V obshem sluchae
trigonometricheskogo mnogochlena men'shei stepeni ne sushestvuet.
V vyrozhdennyh sluchayah my postroili trigonometricheskie mnogochleny
men'shei stepeni, a v sluchae dvoinogo i troinogo vyrozhdeniya poluchili
yavnoe reshenie dlya
. V obshem sluchae
trigonometricheskogo mnogochlena men'shei stepeni ne sushestvuet.
V vyrozhdennyh sluchayah my postroili trigonometricheskie mnogochleny
men'shei stepeni, a v sluchae dvoinogo i troinogo vyrozhdeniya poluchili
yavnoe reshenie dlya ![]() . Podrobnoe reshenie zadachi (s propuskom odnogo iz
vyrozhdennyh sluchaev) soderzhitsya v
[1]. Zdes' my privedem osnovnye rezul'taty.
. Podrobnoe reshenie zadachi (s propuskom odnogo iz
vyrozhdennyh sluchaev) soderzhitsya v
[1]. Zdes' my privedem osnovnye rezul'taty.
Pust'
![]() - keplerovskie elementy
- keplerovskie elementy ![]() ;
;
![]() . Opisyvayushie
. Opisyvayushie ![]() velichiny pomechayutsya shtrihom. Vektor
polozheniya
velichiny pomechayutsya shtrihom. Vektor
polozheniya ![]() na
na ![]() vyrazim cherez ekscentricheskuyu anomaliyu
vyrazim cherez ekscentricheskuyu anomaliyu ![]()
Zdes'
Zdes'
Dlya privedennogo k bezrazmernomu vidu kvadrata funkcii rasstoyaniya
![]() legko vyvesti predstavlenie
legko vyvesti predstavlenie
Zdes'
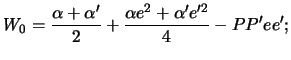
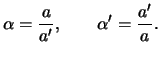
Funkciya (2) yavlyaetsya trigonometricheskim mnogochlenom dvuh
peremennyh ![]() i prinimaet naimen'shee na dvumernom tore znachenie
v odnoi iz kriticheskih tochek, udovletvoryayushih uravneniyam
i prinimaet naimen'shee na dvumernom tore znachenie
v odnoi iz kriticheskih tochek, udovletvoryayushih uravneniyam
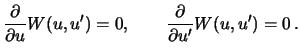
Funkcii
Ispol'zuya algebraicheskuyu tehniku bazisov Grebnera [3], mozhno
isklyuchit' iz uravnenii (3) peremennuyu ![]() . V rezul'tate
poluchaem trigonometricheskii mnogochlen
. V rezul'tate
poluchaem trigonometricheskii mnogochlen ![]() vos'moi stepeni
vos'moi stepeni
Sootnoshenie ![]() neobhodimo i dostatochno dlya sovmestnosti
sistemy (3). V nevyrozhdennom sluchae ne sushestvuet mnogochlena
men'shei stepeni, obladayushego etim svoistvom.
neobhodimo i dostatochno dlya sovmestnosti
sistemy (3). V nevyrozhdennom sluchae ne sushestvuet mnogochlena
men'shei stepeni, obladayushego etim svoistvom.
Dokazatel'stvo sm v [1].
Opishem algoritm opredeleniya ![]() .
Na pervom shage reshaetsya uravnenie
.
Na pervom shage reshaetsya uravnenie ![]() , t.e. nahodyatsya vse ego
veshestvennye korni na okruzhnosti
, t.e. nahodyatsya vse ego
veshestvennye korni na okruzhnosti ![]() . Na vtorom shage ishutsya
sootvetstvuyushie znacheniya
. Na vtorom shage ishutsya
sootvetstvuyushie znacheniya ![]() po formule
po formule
gde
Na tret'em shage sravnivaetsya konechnoe mnozhestvo znachenii ![]() i vybiraetsya naimen'shee
i vybiraetsya naimen'shee ![]() . V rezul'tate
. V rezul'tate
Rassmotrim vyrozhdennye sluchai, kogda kriticheskie tochki otvechayut veshestvennym kornyam trigonometricheskogo uravneniya men'shei stepeni. Intuiciya podskazyvaet, chto prosteishie vyrozhdeniya svyazany s dvumya razlichnymi sluchayami: obrasheniem v nul' vzaimnogo naklona i hotya by odnogo iz ekscentrisitetov. Kak chasto byvaet, intuiciya opravdyvaetsya lish' chastichno. Komplanarnost', v otlichie ot krugovogo sluchaya, ne vedet k vyrozhdeniyu.
1. Pust' orbita ![]() - krugovaya. Bolee togo, dopustimo schitat'
- krugovaya. Bolee togo, dopustimo schitat'
![]() , ne prenebregaya pervoi stepen'yu ekscentrisiteta. Polagaya
, ne prenebregaya pervoi stepen'yu ekscentrisiteta. Polagaya
![]() i ispol'zuya proceduru faktorizacii, predstavim
i ispol'zuya proceduru faktorizacii, predstavim ![]() v forme
v forme
2. Esli ischezayut oba ekscentrisiteta ![]() , to
, to ![]() i
i
Bolee togo, ![]() soderzhit tol'ko vtorye garmoniki
soderzhit tol'ko vtorye garmoniki
3. Esli v komplanarnom sluchae orbita ![]() - krugovaya, to
- krugovaya, to
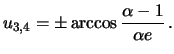
4. Nakonec, obrashenie v nul' oboih ekscentrisitetov i vzaimnogo naklona vlechet maksimal'no vyrozhdennyi sluchai
<< 1. Vvedenie | Oglavlenie | 3. Topologiya par orbit >>
|
Publikacii s klyuchevymi slovami:
Nebesnaya mehanika - keplerovy orbity
Publikacii so slovami: Nebesnaya mehanika - keplerovy orbity | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |