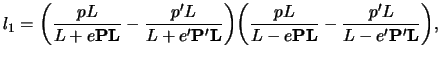Topologiya i metrika par keplerovskih orbit
<< 2. Evklidovo rasstoyanie mezhdu orbitami | Oglavlenie | 4. Estestvennye metriki v ... >>
3. Topologicheskoe raspolozhenie par keplerovskih orbit
v
prostranstve
Para ellipsov obshego polozheniya mozhet byt' vlozhena v trehmernoe
prostranstvo dvumya topologicheski razlichnymi sposobami. Oni mogut byt'
scepleny (sluchai ![]() ) i net (sluchai
) i net (sluchai ![]() ). Vyrozhdennyi sluchai
peresecheniya
). Vyrozhdennyi sluchai
peresecheniya ![]() razdelyaet
razdelyaet ![]() i
i ![]() .
Algebraicheskaya topologiya operiruet s koefficientom zacepleniya
.
Algebraicheskaya topologiya operiruet s koefficientom zacepleniya
![]() , opredelennym na kazhdoi pare topologicheskih
okruzhnostei i ravnym
, opredelennym na kazhdoi pare topologicheskih
okruzhnostei i ravnym ![]() v sluchayah
v sluchayah ![]() sootvetstvenno.
sootvetstvenno.
Na praktike eta razryvnaya funkciya neudobna. Dlya nekomplanarnyh orbit
my predlagaem prostoi nepreryvnyi analog ![]() velichiny
velichiny ![]() ,
otricatel'nyi, polozhitel'nyi i ravnyi nulyu v vysheperechislennyh sluchayah
i nesushii dopolnitel'nye svedeniya o rasstoyanii mezhdu orbitami. Dlya
blizkih k peresecheniyu orbit
,
otricatel'nyi, polozhitel'nyi i ravnyi nulyu v vysheperechislennyh sluchayah
i nesushii dopolnitel'nye svedeniya o rasstoyanii mezhdu orbitami. Dlya
blizkih k peresecheniyu orbit ![]() malo.
T.k. kriterii
malo.
T.k. kriterii ![]() ne goditsya v komplanarnom sluchae, my vvodim takzhe
dva dopolnitel'nyh kriteriya
ne goditsya v komplanarnom sluchae, my vvodim takzhe
dva dopolnitel'nyh kriteriya ![]() i
i ![]() .
.
1. Prostranstvennyi sluchai. Pust' orbity ![]() nekomplanarny. Togda
vektor
nekomplanarny. Togda
vektor
![]() parallelen linii vzaimnyh uzlov i
parallelen linii vzaimnyh uzlov i
![]() . Ochevidno,
. Ochevidno,
Radiusy
On ne zavisit ot koordinatnoi sistemy. Krome togo,
gde
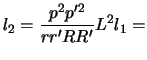
V sluchae
2. Komplanarnyi sluchai. Esli vzaimnyi naklon raven nulyu, to
![]() ne opredelen, a
ne opredelen, a ![]() raven nulyu. My ne mozhem razlichit' sluchai
raven nulyu. My ne mozhem razlichit' sluchai
![]() i
i ![]() (sluchai
(sluchai ![]() ne vstrechaetsya v dvumernom prostranstve).
Chtoby zapolnit' lakunu, vvedem tretii koefficient
ne vstrechaetsya v dvumernom prostranstve).
Chtoby zapolnit' lakunu, vvedem tretii koefficient
imeyushii smysl tol'ko v komplanarnom sluchae.
Imenno, ![]() , esli
, esli ![]() ,
, ![]() ne peresekayutsya (sluchai
ne peresekayutsya (sluchai ![]() );
);
![]() - v protivopolozhnom sluchae
- v protivopolozhnom sluchae ![]() . Tochnee,
. Tochnee,
![]() otvechaet transversal'nomu peresecheniyu v dvuh tochkah;
otvechaet transversal'nomu peresecheniyu v dvuh tochkah;
![]() otvechaet edinstvennoi obshei tochke, v kotoroi
otvechaet edinstvennoi obshei tochke, v kotoroi ![]() ,
, ![]() kasayutsya drug druga, ili naibolee vyrozhdennomu sluchayu
kasayutsya drug druga, ili naibolee vyrozhdennomu sluchayu ![]() . Stoit
zametit', chto
. Stoit
zametit', chto ![]() nepreryven na mnozhestve par komplanarnyh
ellipsov.
nepreryven na mnozhestve par komplanarnyh
ellipsov.
Iz svoistv ![]() mozhno poputno vyvesti zaklyuchenie o chisle
tochek peresecheniya keplerovskih orbit
mozhno poputno vyvesti zaklyuchenie o chisle
tochek peresecheniya keplerovskih orbit ![]() .
.
Sushestvuet pyat' i tol'ko pyat' variantov:
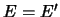 .
.
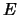 i
i 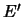 imeyut obshuyu chast', hotya
imeyut obshuyu chast', hotya 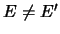 . Eto vozmozhno
tol'ko v sluchae dvuh pryamolineinyh orbit.
. Eto vozmozhno
tol'ko v sluchae dvuh pryamolineinyh orbit.
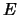 i
i 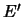 imeyut rovno dve obshie tochki, v oboih peresechenie
transversal'no.
imeyut rovno dve obshie tochki, v oboih peresechenie
transversal'no.
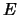 i
i 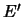 imeyut rovno odnu obshuyu tochku, v kotoroi
imeyut rovno odnu obshuyu tochku, v kotoroi 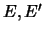 transversal'no peresekayutsya ili kasayutsya. V poslednem sluchae oni
lezhat v odnoi ploskosti i odna iz nih lezhit vnutri drugoi.
transversal'no peresekayutsya ili kasayutsya. V poslednem sluchae oni
lezhat v odnoi ploskosti i odna iz nih lezhit vnutri drugoi.
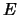 i
i 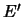 ne imeyut obshih tochek.
ne imeyut obshih tochek.
<< 2. Evklidovo rasstoyanie mezhdu orbitami | Oglavlenie | 4. Estestvennye metriki v ... >>
|
Publikacii s klyuchevymi slovami:
Nebesnaya mehanika - keplerovy orbity
Publikacii so slovami: Nebesnaya mehanika - keplerovy orbity | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |