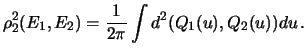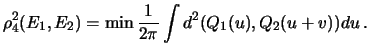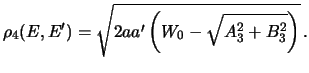Topologiya i metrika par keplerovskih orbit

---

<< 3. Topologiya par orbit | Oglavlenie | 5. Pochti peresekayushiesya orbity >>

4. Estestvennye metriki v prostranstve keplerovskih orbit

Budem teper' schitat' tochkoi v pyatimernom prostranstve keplerovskih ellipsov. Postroim neskol'ko estestvennyh metrik v . Malost' oznachaet, chto orbity pochti sovpadayut.

Dlya postroeniya rasstoyaniya predstavlyaetsya estestvennym sravnivat' tochki s odinakovoi ekscentricheskoi anomaliei. Takim putem poluchaem ravnomernuyu i srednekvadraticheskuyu metriki

Naibol'shee znachenie i integral berutsya po otrezku .

Legko dokazat', chto vse aksiomy metricheskogo prostranstva vypolneny dlya obeih metrik (10), (11), esli isklyuchit' krugovye orbity. Inymi slovami, rasstoyaniya (10), (11) opredeleny i topologicheski ekvivalentny v prostranstve nekrugovyh ellipticheskih orbit. Oni razryvny v okrestnosti hotya by odnoi krugovoi orbity iz pary. Prichina ochevidna. Naprimer, dve komplanarnye orbity s odinakovoi bol'shoi poluos'yu i pochti nulevymi ekscentrisitetami pochti sovpadayut nezavisimo ot napravleniya apsid. No oba rasstoyaniya sushestvenno zavisyat ot ih napravleniya.

Chtoby izbezhat' nepriyatnostei, my dolzhny sravnivat' tochki, imeyushie razlichnye vzaimnye polozheniya. Horoshii sposob - vvesti sleduyushie metriki:

Naibol'shee znachenie i integral berutsya po otrezku , naimen'shee znachenie - po otrezku .

Vse aksiomy metricheskogo prostranstva vypolneny dlya obeih metrik (12), (13) vo vsem prostranstve , hotya dokazatel'stvo mnogo slozhnee, chem v predydushem sluchae. Rasstoyaniya (12), (13) topologicheski ekvivalentny i prevrashayut v otkrytoe, neogranichennoe, lokal'no-kompaktnoe metricheskoe prostranstvo.

Privedem algoritmy opredeleniya rasstoyanii .

1. Oboznachim . Ochevidno,

gde

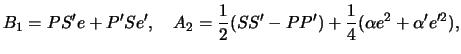
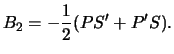
Pervyi shag sostoit v nahozhdenii vseh veshestvennyh, lezhashih na okruzhnosti kornei uravneniya

gde

Oboznachim cherez odin iz kornei (15), dayushii naibol'shee znachenie . Togda

2. Integral (11) elementaren. Dlya vtorogo rasstoyaniya poluchaem prostuyu formulu

3. Algoritm vychisleniya tret'ego rasstoyaniya stol' slozhen, chto my ne rekomenduem ispol'zovat' na praktike.

4. Integral v (13) elementaren

Zdes'

gde

Poskol'ku , poluchaem okonchatel'no

---

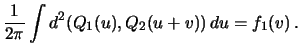
<< 3. Topologiya par orbit | Oglavlenie | 5. Pochti peresekayushiesya orbity >>

Publikacii s klyuchevymi slovami: Nebesnaya mehanika - keplerovy orbity Publikacii so slovami: Nebesnaya mehanika - keplerovy orbity

Sm. takzhe: Saimon N'yukom (1835 -1909) k 175-letiyu so dnya rozhdeniya. Naum Il'ich Idel'son - 125 let so dnya rozhdeniya Metody teorii special'nyh vozmushenii v nebesnoi mehanike Zadacha N tel i problema integriruemosti K 90-letiyu Aleksandra Aleksandrovicha Orlova Dinamika zvezdnyh skoplenii Prosteishaya forma predstavleniya gradienta gravitacionnogo potenciala nebesnyh tel Vse publikacii na tu zhe temu >>