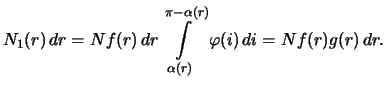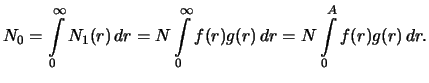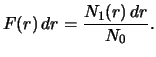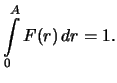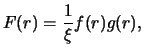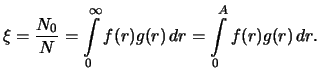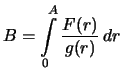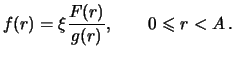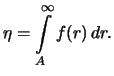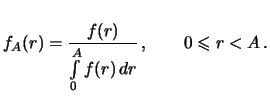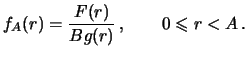O raspredelenii bol'shih poluosei orbit vnesolnechnyh planet
<< 3. Veroyatnost' obnaruzheniya planety
| Oglavlenie |
5. Chislennye rezul'taty >>
Effekt selekcii otrazhen formuloi (
4): planet, imeyushih
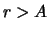
, my ne vidim sovsem; pri
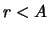
shansy planety byt'
obnaruzhennoi stremitel'no rastut s umen'sheniem

. S rostom
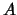
(t. e. s uvelicheniem
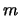
i umen'sheniem oshibki nablyudenii
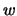
)
effekt selekcii umen'shaetsya.
Polnost'yu effekt selekcii vyyavlyaetsya v transformacii funkcii
raspredeleniya.
Pust' imeetsya bol'shoe chislo
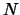
nablyudennyh zvezd, imeyushih kazhdaya po
planete s krugovoi orbitoi. Poka v nashem rasporyazhenii slishkom malo
dannyh,
chtoby operirovat' s mnogomernymi raspredeleniyami
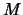
,
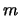
,

,
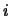
.
Ogranichimsya prosteishei odnomernoi zadachei. Imenno, fiksiruem
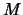
,
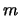
;
predpolozhim nezavisimost' raspredelenii

,
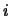
; izotropnost'
orientacii
vektora ploshadei. Togda statisticheskaya situaciya polnost'yu opisyvaetsya
plotnost'yu veroyatnosti
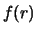
: chislo planet s rasstoyaniem ot

do
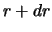
ravno
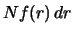
.
Naidem plotnost' veroyatnosti
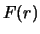
velichiny
 sredi otkrytyh
planet
sredi otkrytyh
planet.
Ochevidno, chislo planet s rasstoyaniyami ot

do
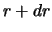
i naklonami ot
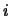
do
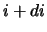
ravno
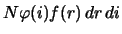
. Chislo
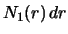
otkrytyh
planet s rasstoyaniyami mezhdu

i
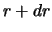
ravno
Chislo vseh otkrytyh planet
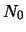
est'
Dolya otkrytyh planet s rasstoyaniyami ot

do
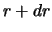
sredi vseh otkrytyh
planet est'
Okonchatel'no,
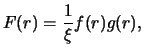 |
(5) |
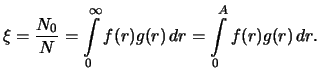 |
(6) |
Velichina
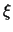
sovpadaet s veroyatnost'yu otkrytiya planety s dannymi
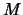
,
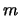
i sluchainymi
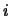
,

. Obratim vnimanie, chto
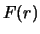
ravna nulyu pri
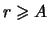
.
Formuly (
4)-(
6) konstruktivno opredelyayut
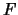
, esli
izvestna
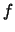
. Odnako otnositel'no
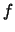
my mozhem poka lish' stroit'
dogadki. V to zhe vremya
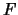
mozhet byt' naidena (pust' poka ne ochen'
uverenno) iz nablyudenii.
Reshim obratnuyu zadachu postroeniya
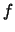
po izvestnoi
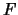
.
Dana nepreryvnaya neotricatel'naya funkciya
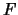
, opredelennaya na
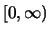
,
ravnaya nulyu na
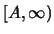
i takaya, chto integral
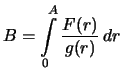 |
(7) |
shoditsya. Tak kak
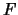
- plotnost' veroyatnosti, to potrebuem eshe
Iz (
5) sleduet
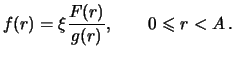 |
(8) |
Legko proverit', chto (
6) vypolnyaetsya pri lyubom
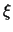
, esli
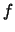
opredelyaetsya ravenstvom (
8). Chtoby naiti
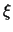
, vychislim
integral ot obeih chastei (
8) po promezhutku
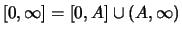
:
gde
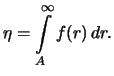 |
(9) |
Fiksiruem proizvol'noe
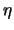
,
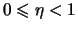
. Togda
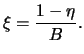 |
(10) |
Tak kak
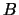
izvestno, to formula (
10) opredelyaet polozhitel'noe
chislo
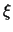
, posle chego (
8) daet nam
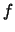
pri
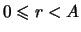
.
Itak, my nashli
vse funkcii
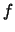
, dayushie nablyudaemuyu plotnost'
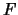
. Pravee tochki
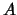
raspredelenie
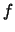
neizvestno. Levee funkciya
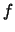
opredelena s tochnost'yu do mnozhitelya
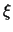
. Eto vazhnaya
informaciya, t. k. ona soderzhit ischerpyvayushie svedeniya o
raspredelenii rasstoyanii

sredi vseh planet, raspolozhennyh ne
dalee
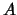
ot svoei zvezdy.
Deistvitel'no, oboznachim cherez
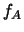
sootvetstvuyushuyu plotnost'
veroyatnosti. Po opredeleniyu
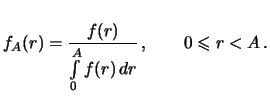 |
(11) |
Podstavlyaya v chislitel' i znamenatel' sleduyushee iz (
5) vyrazhenie
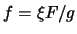
, poluchim iskomoe
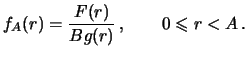 |
(12) |
Iz (
11), (
9) vytekayut poleznye sootnosheniya
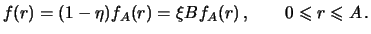 |
(13) |
Sleduet pomnit', chto
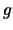
bezrazmerna,
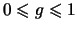
;
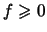
,
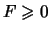
,
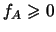
imeyut razmernost'
[m
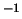
];
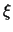
,
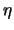
i
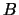
bezrazmerny, svyazany sootnosheniem
(
10), prichem
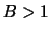
,
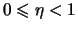
,
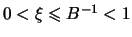
.
<< 3. Veroyatnost' obnaruzheniya planety
| Oglavlenie |
5. Chislennye rezul'taty >>