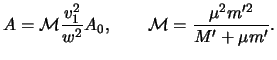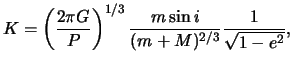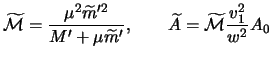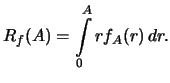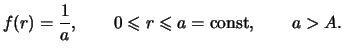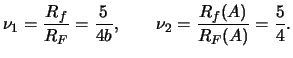O raspredelenii bol'shih poluosei orbit vnesolnechnyh planet
<< 4. Funkcii raspredeleniya | Oglavlenie | 6. Zaklyuchenie >>
5. Chislennye rezul'taty
Issleduem oblast' obnaruzhimostiZdes'
Tablica 1.
Znacheniya privedennoi massy planety 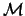 i kriticheskogo
rasstoyaniya
i kriticheskogo
rasstoyaniya 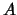 (a.e.)
(a.e.)
v zavisimosti ot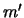 i
i 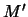 pri
pri
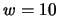 m/s
m/s
v zavisimosti ot
|
|
|
|||||
| 0.25 | 0.50 | 0.75 | 1.00 | 1.25 | 1.50 | |
| M9 | M0 | K0 | G2 | F6 | F1 | |
| 10 |
|
|
|
|
|
|
| 3000 | 2000 | 1000 | 800 | 600 | 500 | |
| 1 |
|
|
|
|
|
|
| (Yupiter) | 30 | 20 | 10 | 8 | 6 | 5 |
| 0.3 |
|
|
|
|
|
|
| (Saturn) | 3 | 1 | 1 | 0.7 | 0.6 | 0.5 |
| 0.05 |
|
|
|
|
|
|
| (Uran, Neptun) | 0.08 | 0.04 | 0.03 | 0.02 | 0.02 | 0.01 |
| 0.003 |
|
|
|
|
|
|
| (Venera, Zemlya) |
|
|
|
|
|
|
| 0.0002 |
|
|
|
|
|
|
| (Merkurii) |
|
|
|
|
|
|
Privedennaya massa
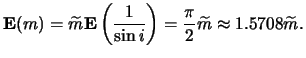
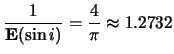
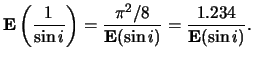
gde
i veroyatnosti
nedostatochna dlya obnaruzheniya planet s massoi
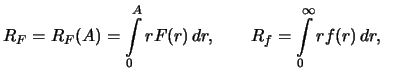
Tablica 2.
Parametry vnesolnechnyh planetnyh sistem.
Rasstoyaniya dany v a.e., skorosti - v m/s
| Zvezda | |
|
|
|
|
|
|
|
|
| HD 83443 b | 0.82 | 0.34 |
|
0.038 | 0.08 | 57.0 | 1.1 | 12.6 | 0.98 |
| HD 46375 | 1.00 | 0.25 |
|
0.041 | 0.02 | 35.2 | 0.5 | 5.6 | 0.96 |
| HD 179949 | 1.24 | 0.93 |
|
0.045 | 0.00 | 112.0 | 5.7 | 62.8 | 1.00 |
| HD 187123 | 1.00 | 0.54 |
|
0.042 | 0.01 | 72.0 | 2.4 | 26.2 | 0.99 |
|
|
1.20 | 4.14 |
|
0.047 | 0.02 | 474.0 | 115.7 | 1285.6 | 1.00 |
|
BD |
1.10 | 0.48 |
|
0.046 | 0.05 | 60.6 | 1.7 | 18.9 | 0.99 |
| HD 75289 | 1.05 | 0.46 |
|
0.048 | 0.00 | 54.0 | 1.6 | 18.1 | 0.99 |
| HD 209458 | 1.03 | 0.63 |
|
0.046 | 0.02 | 82.0 | 3.1 | 34.7 | 0.99 |
| 51 Peg | 0.98 | 0.46 |
|
0.052 | 0.01 | 55.2 | 1.7 | 19.4 | 0.99 |
|
|
1.10 | 0.68 |
|
0.059 | 0.02 | 70.2 | 3.4 | 37.8 | 0.99 |
| HD 68988 | 1.20 | 1.90 |
|
0.071 | 0.14 | 187.0 | 24.4 | 270.8 | 1.00 |
| HD 168746 | 0.94 | 0.24 |
|
0.066 | 0.00 | 28.0 | 0.5 | 5.5 | 0.93 |
| HD 217107 | 0.96 | 1.29 |
|
0.072 | 0.14 | 139.7 | 14.0 | 156.0 | 1.00 |
| HD 162020 | 0.70 | 13.73 |
|
0.072 | 0.28 | 1813.0 | 2174.3 | 24158.8 | 1.00 |
| HD 130322 | 0.79 | 1.15 |
|
0.092 | 0.05 | 115.0 | 13.6 | 150.7 | 1.00 |
| HD 108147 | 1.06 | 0.35 |
|
0.098 | 0.56 | 37.0 | 0.9 | 10.4 | 0.95 |
| HD 38529 | 1.40 | 0.77 |
|
0.129 | 0.27 | 53.6 | 3.4 | 38.2 | 0.98 |
| 55 Cnc | 0.90 | 0.93 |
|
0.118 | 0.03 | 75.8 | 7.8 | 86.5 | 0.99 |
| HD 13445 = GJ 86 | 0.79 | 4.23 |
|
0.117 | 0.04 | 379.0 | 183.5 | 2038.6 | 1.00 |
| HD 195019 | 0.98 | 3.55 |
|
0.136 | 0.01 | 271.0 | 104.2 | 1157.5 | 1.00 |
| HD 6434 | 1.00 | 0.48 |
|
0.154 | 0.30 | 37.0 | 1.9 | 20.8 | 0.96 |
| HD 192263 | 0.75 | 0.81 |
|
0.152 | 0.22 | 68.2 | 7.1 | 78.7 | 0.99 |
| HD 83443 c | 0.79 | 0.17 |
|
0.174 | 0.42 | 14.0 | 0.3 | 3.3 | 0.64 |
| GJ 876 c | 0.32 | 0.56 |
|
0.130 | 0.27 | 81.0 | 7.9 | 88.2 | 0.99 |
|
|
1.00 | 0.99 |
|
0.224 | 0.07 | 61.3 | 7.9 | 88.2 | 0.99 |
| HD 74156 b | 1.05 | 1.55 |
|
0.276 | 0.65 | 108.0 | 18.5 | 205.4 | 0.99 |
| HD 168443 b | 0.84 | 7.64 |
|
0.295 | 0.53 | 470.0 | 562.9 | 6254.5 | 1.00 |
| GJ 876 b | 0.32 | 1.89 |
|
0.207 | 0.10 | 210.0 | 90.4 | 1004.8 | 1.00 |
| HD 121504 | 1.02 | 0.89 |
|
0.317 | 0.13 | 45.0 | 6.3 | 70.1 | 0.97 |
| HD 178911 b | 0.90 | 6.46 |
|
0.326 | 0.14 | 343.0 | 373.9 | 4154.6 | 1.00 |
| HD 16141 | 0.99 | 0.22 |
|
0.351 | 0.28 | 10.8 | 0.4 | 4.4 | 0.34 |
| HD 114762 | 0.82 | 10.96 |
|
0.351 | 0.33 | 615.0 | 1186.7 | 13185.5 | 1.00 |
| HD 80606 | 0.90 | 3.43 |
|
0.438 | 0.93 | 414.0 | 106.3 | 1180.7 | 1.00 |
| 70 Vir | 1.10 | 7.42 |
|
0.482 | 0.40 | 316.2 | 405.5 | 4505.1 | 1.00 |
| HD 52265 | 1.13 | 1.14 |
|
0.493 | 0.29 | 45.4 | 9.3 | 103.5 | 0.97 |
| HD 1237 | 0.98 | 3.45 |
|
0.505 | 0.51 | 164.0 | 98.4 | 1093.2 | 1.00 |
| HD 37124 | 0.91 | 1.13 |
|
0.547 | 0.31 | 48.0 | 11.4 | 126.3 | 0.98 |
| HD 82943 c | 1.05 | 0.88 |
|
0.728 | 0.54 | 34.0 | 6.0 | 66.5 | 0.94 |
| HD 8574 | 1.10 | 2.23 |
|
0.756 | 0.40 | 76.0 | 36.6 | 406.5 | 0.99 |
| HD 169830 | 1.40 | 2.95 |
|
0.823 | 0.34 | 83.0 | 50.3 | 559.1 | 0.99 |
|
|
1.10 | 2.05 |
|
0.828 | 0.24 | 58.0 | 30.9 | 343.9 | 0.99 |
| HD 12661 | 0.81 | 2.84 |
|
0.795 | 0.19 | 89.1 | 80.7 | 896.3 | 1.00 |
| HD 89744 | 1.40 | 7.17 |
|
0.883 | 0.70 | 257.0 | 297.5 | 3305.2 | 1.00 |
| HD 202206 | 0.90 | 14.68 |
|
0.768 | 0.42 | 554.0 | 1936.3 | 21514.9 | 1.00 |
| HD 134987 | 1.05 | 1.58 |
|
0.810 | 0.24 | 50.2 | 19.3 | 214.0 | 0.98 |
|
HD 17051 = |
1.03 | 2.98 |
|
0.970 | 0.16 | 80.0 | 69.8 | 776.0 | 0.99 |
| HD 92788 | 1.06 | 3.88 |
|
0.969 | 0.28 | 113.0 | 115.1 | 1278.3 | 1.00 |
| HD 142 | 1.10 | 1.36 |
|
0.980 | 0.37 | 40.0 | 13.6 | 151.3 | 0.96 |
| HD 28185 | 0.90 | 5.59 |
|
1.000 | 0.06 | 168.0 | 281.3 | 3125.0 | 1.00 |
| HD 177830 | 1.15 | 1.24 |
|
1.100 | 0.40 | 34.0 | 10.8 | 120.3 | 0.95 |
| HD 4203 | 1.06 | 1.64 |
|
1.090 | 0.53 | 51.0 | 20.6 | 228.4 | 0.97 |
| HD 27442 | 1.20 | 1.42 |
|
1.180 | 0.02 | 34.0 | 13.6 | 151.2 | 0.96 |
| HD 210277 | 0.92 | 1.29 |
|
1.120 | 0.45 | 39.1 | 14.7 | 162.8 | 0.96 |
| HD 82943 b | 1.05 | 1.63 |
|
1.160 | 0.41 | 46.0 | 20.4 | 227.0 | 0.97 |
| HD 19994 | 1.29 | 1.83 |
|
1.260 | 0.20 | 42.0 | 21.0 | 233.0 | 0.97 |
| HD 114783 | 0.92 | 0.99 |
|
1.200 | 0.10 | 27.0 | 8.6 | 95.9 | 0.93 |
| HD 222582 | 1.00 | 5.18 |
|
1.350 | 0.71 | 179.6 | 217.4 | 2415.2 | 1.00 |
| HD 23079 | 1.10 | 2.76 |
|
1.480 | 0.03 | 62.0 | 56.1 | 623.3 | 0.99 |
| HD 141937 | 1.00 | 9.69 |
|
1.480 | 0.40 | 247.0 | 763.3 | 8481.6 | 1.00 |
| HD 160691 | 1.08 | 1.99 |
|
1.650 | 0.62 | 54.0 | 29.7 | 330.0 | 0.97 |
| HD 213240 | 0.95 | 3.75 |
|
1.600 | 0.31 | 91.0 | 120.1 | 1334.4 | 0.99 |
| 16 Cyg B | 1.00 | 1.68 |
|
1.690 | 0.68 | 50.0 | 22.9 | 254.0 | 0.96 |
| HD 4208 | 0.93 | 0.81 |
|
1.690 | 0.04 | 18.3 | 5.7 | 63.5 | 0.84 |
| HD 10697 | 1.10 | 6.08 |
|
2.120 | 0.11 | 114.0 | 272.2 | 3024.8 | 1.00 |
| 47 UMa b | 1.03 | 2.54 |
|
2.090 | 0.06 | 49.3 | 50.7 | 563.8 | 0.98 |
| HD 190228 | 1.20 | 5.01 |
|
2.250 | 0.43 | 96.0 | 170.0 | 1888.4 | 0.99 |
| HD 50554 | 1.10 | 4.91 |
|
2.380 | 0.42 | 95.0 | 177.6 | 1973.7 | 0.99 |
|
|
1.10 | 4.29 |
|
2.560 | 0.31 | 70.4 | 135.5 | 1505.9 | 0.99 |
| HD 33636 | 0.99 | 7.71 |
|
2.620 | 0.39 | 148.0 | 486.4 | 5404.6 | 1.00 |
| HD 106252 | 1.05 | 6.81 |
|
2.610 | 0.54 | 139.0 | 356.4 | 3959.7 | 1.00 |
| HD 168443 c | 0.84 | 16.96 |
|
2.870 | 0.20 | 289.0 | 2774.0 | 30821.9 | 1.00 |
| 14 Her | 0.85 | 4.05 |
|
3.170 | 0.45 | 70.4 | 156.3 | 1736.9 | 0.99 |
| HD 39091 | 1.10 | 9.94 |
|
3.500 | 0.67 | 194.0 | 727.6 | 8084.8 | 1.00 |
| HD 74156 c | 1.05 | 7.46 |
|
3.470 | 0.40 | 121.0 | 427.9 | 4753.9 | 1.00 |
|
|
0.80 | 0.88 |
|
3.360 | 0.60 | 19.0 | 7.8 | 87.1 | 0.76 |
| 47 UMa c | 1.03 | 0.76 |
|
3.730 | 0.10 | 11.1 | 4.5 | 50.5 | 0.42 |
Primer.
Ravnomernoe raspredelenie:Vychislim plotnosti veroyatnosti
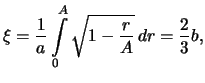
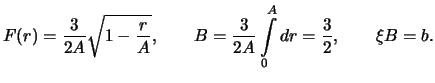
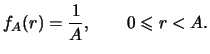
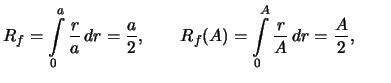
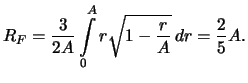
Iz (19) sleduet, chto pri malyh
<< 4. Funkcii raspredeleniya | Oglavlenie | 6. Zaklyuchenie >>
|
Publikacii s klyuchevymi slovami:
ekzoplaneta
Publikacii so slovami: ekzoplaneta | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |
Astrometriya
-
Astronomicheskie instrumenty
-
Astronomicheskoe obrazovanie
-
Astrofizika
-
Istoriya astronomii
-
Kosmonavtika, issledovanie kosmosa
-
Lyubitel'skaya astronomiya
-
Planety i Solnechnaya sistema
-
Solnce