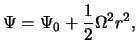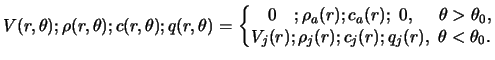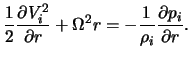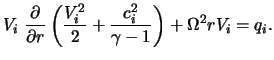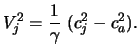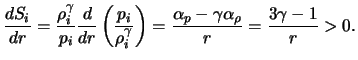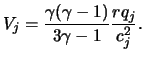Regulyarnye struktury v konusah ionizacii v okrestnosti aktivnyh yader galaktik

---

<< 1. Vvedenie | Oglavlenie | 3. Metodika nelineinogo modelirovaniya >>

2. Ravnovesnaya model', osnovnye uravneniya
i rezul'taty lineinogo analiza ustoichivosti

Obosnovanie primenyaemoi ravnovesnoi modeli i ee postroenie podrobno opisany nami v [1], poetomu zdes' my prodelaem eto konspektivno.

Rassmotrenie provodim v sfericheskoi sisteme koordinat , os' kotoroi sovpadaet s os'yu simmetrii strui, imeyushei ugol polurastvora i skorost' techeniya , gde - edinichnyi radial'nyi bazisnyi vektor. Sredu modeliruem ideal'nym gazom s uravneniem sostoyaniya

gde i - nevozmushennye (ravnovesnye) davlenie i plotnost' sootvetstvenno; - adiabaticheskaya skorost' zvuka; indeks prinimaet znachenie vnutri strui i snaruzhi; pokazatel' adiabaty predpolagaem odinakovym dlya veshestva strui i okruzhayushego ee gaza.

V okoloyadernoi oblasti struya pogruzhena v raspredelennuyu massu zvezdnogo baldzha, kotoryi v pervom priblizhenii mozhno schitat' sferoidal'nym; krome togo, dlya galaktik rassmatrivaemogo tipa (naprimer, NGC 5252) voobshe harakterna moshnaya sferoidal'naya podsistema. Na uchastke, sovpadayushem po radial'noi koordinate s uchastkom tverdotel'nogo vrasheniya galakticheskogo diska, gravitacionnyi potencial mozhno s horoshei tochnost'yu polagat' kvadratichnym po radiusu: . Schitaem gravitacionnoe pole sfericheski simmetrichnym, s centrom, sovpadayushim s nachalom koordinat. Radial'nuyu zavisimost' gravitacionnogo potenciala predstavim sleduyushim obrazom:

gde - uglovaya skorost' vrasheniya gaza v okoloyadernoi oblasti diska, - normirovochnaya postoyannaya.

Gaz vne strui schitaem nepodvizhnym. Uchtem vozmozhnost' nagreva gaza strui izlucheniem yadra: , gde - kolichestvo energii, pogloshaemoe edinicei massy veshestva v edinicu vremeni; - funkciya nagreva, - funkciya ohlazhdeniya, zavisyashie tol'ko ot temperatury . V ravnovesnom sostoyanii vne strui .

Prostranstvennoe raspredelenie harakterizuyushih nevozmushennoe techenie parametrov modeli imeet vid

Polagaem, chto struya uderzhivaetsya davleniem okruzhayushego gaza i, sledovatel'no, pri vypolnyaetsya

Poslednee sootnoshenie dalee prakticheski ne ispol'zuetsya neposredstvenno; ego vypolnenie neobhodimo dlya realizacii techeniya s .

Radial'nye zavisimosti v (3) opredelyayutsya nevozmushennym balansom sil. Iz -komponenty uravneniya Eilera v prinyatyh predpolozheniyah sleduet

Iz uravneniya nerazryvnosti vytekaet

V uravnenii (6) - temp poteri massy sistemoi v telesnyi ugol rastvorom v odin steradian - yavlyaetsya svobodnym parametrom.

Uravnenie balansa energii s uchetom (1) i uravneniya nerazryvnosti dlya rassmatrivaemogo sluchaya privoditsya k vidu

Sistema (4)-(7) zamykaetsya uravneniem sostoyaniya (1).

Resheniya etoi sistemy ishem v stepennom vide: , gde  - lyuboi iz parametrov, harakterizuyushih sistemu. Iz (5) s uchetom (1) sleduet ; sootvetstvenno nahodim

Dlya sfericheski simmetrichnogo potenciala skorost' veshestva
v strue i skorosti zvuka v strue i v okruzhayushei ee atmosfere okazyvayutsya svyazany zavisimost'yu

Takim obrazom, , gde - chislo Maha strui, t. e. struya dozvukovaya. Odnovremenno s etim mozhet vypolnyat'sya dazhe , chto delaet teoreticheski vozmozhnym sushestvovanie udarnyh voln v okruzhayushei struyu srede, obuslovlennyh razvitiem neustoichivosti na granice strui, poskol'ku , t. e. veshestvo strui vsegda bolee goryachee i razrezhennoe, chem okruzhayushaya sreda, chto ne protivorechit nablyudeniyam [2]-[5].

S uchetom togo, chto , postroennaya model' otvechaet ustoichivomu k konvektivnym dvizheniyam raspredeleniyu entropii , poskol'ku

Podstanovka stepennyh radial'nyh zavisimostei v (5) i (7) i sravnenie poluchennyh vyrazhenii privodit k sleduyushemu rezul'tatu:

Takim obrazom, skorost' veshestva v strue odnoznachno opredelyaetsya ego temperaturoi i nagrevom vneshnim izlucheniem. Dlya vybrosov iz aktivnyh yader galaktik poslednii ves'ma znachitelen, tak kak oni intensivno podsvechivayutsya izlucheniem yadra [2]-[5].

Uchityvaya (8) opredelyaem, chto dlya realizacii postroennoi modeli neobhodimo

gde i - postoyannye; - vnutrennyaya energiya gaza (dlya dal'neishih vykladok udobnee vyrazit' nagrev i ohlazhdenie ne cherez temperaturu, a cherez vnutrennyuyu energiyu, ispol'zuya tot fakt, chto dlya ideal'nogo gaza ). Vtoroe sootnoshenie v (12) v shirokom diapazone temperatur (prakticheski do ) velikolepno soglasuetsya s zavisimost'yu , harakternoi dlya fotoionizovannogo gaza seifertovskih galaktik [9], [15]. Lineinaya zavisimost' funkcii nagreva ot temperatury takzhe yavlyaetsya horoshei approksimaciei.

Dalee rassmatrivaetsya ustoichivost' postroennoi nami modeli k malym vozmusheniyam vida

Ishodya iz neobhodimosti sohraneniya potoka energii vozmushenii cherez sferu proizvol'nogo radiusa ( ), opredelyaem, chto pokazatel' stepeni radial'nyh zavisimostei amplitud vozmushenii , gde - po-prezhnemu pokazatel' stepeni dlya ravnovesnyh velichin; - pokazatel' stepeni dlya gravitacionnogo potenciala. Vazhno, chto resheniya linearizovannoi sistemy uravnenii gazovoi dinamiki vida (13) yavlyayutsya tochnymi.

Provedennyi lineinyi analiz ustoichivosti pozvolil nam sdelat' sleduyushie vyvody:

1. Konicheskie vybrosy veshestva, nahodyashiesya v pole kvadratichnogo gravitacionnogo potenciala i podobnye nablyudaemym v ryade seifertovskih galaktik, neustoichivy otnositel'no rezonansno-volnovodnogo razvitiya shirokogo spektra pinchevyh i vintovyh vnutrennih gravitacionnyh mod.

2. Harakternoe vremya rosta amplitudy etih mod kraine slabo zavisit ot ugla rastvora strui v shirokom diapazone uglov.

3. Dinamicheskoe ohlazhdenie vysvechivaniem polnost'yu podavlyaet vse gravitacionno-akusticheskie mody, slabo vliyaet na neustoichivye poverhnostnye mody Kel'vina-Gel'mgol'ca, privodit k zatuhaniyu volnovodno-rezonansnyh vnutrennih gravitacionnyh mod, rasprostranyayushihsya otnositel'no veshestva strui ot istochnika vybrosa, i, naoborot, znachitel'no usilivaet neustoichivost' takih mod, rasprostranyayushihsya k istochniku.

4. Ukazannoe usilenie imeet harakter radiativno-dissipativnoi neustoichivosti mod otricatel'noi plotnosti energii.

5. Za formirovanie nablyudaemyh regulyarnyh struktur v konusah izlucheniya v okrestnosti yader seifertovskih galaktik mogut byt' otvetstvenny tol'ko poverhnostnye neustoichivye mody i medlennye (rasprostranyayushiesya po strue k istochniku) volnovodno-rezonansnye vnutrennie gravitacionnye mody. Skorosti etih mod vdol' granic strui prevyshayut harakternuyu skorost' zvuka v okruzhayushei atmosfere, chto pozvolyaet predpolagat' vozmozhnost' ih evolyucii v udarnye volny.

6. Pri malyh uglah rastvora strui naibolee veroyatno razvitie osnovnoi garmoniki pinchevoi mody vnutrennih gravitacionnyh voln v korotkovolnovoi oblasti (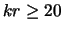), a v bolee dlinnovolnovom diapazone ( 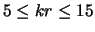) - osnovnoi garmoniki pervoi vintovoi mody.

   Iz-za razlichnoi prostranstvennoi lokalizacii pervoi vintovoi i pinchevoi mod razvitie odnoi iz nih ne dolzhno fatal'no skazyvat'sya na drugoi.

---

<< 1. Vvedenie | Oglavlenie | 3. Metodika nelineinogo modelirovaniya >>

Publikacii s klyuchevymi slovami: Yadra galaktik - dzhet - Seifertovskaya galaktika Publikacii so slovami: Yadra galaktik - dzhet - Seifertovskaya galaktika
Sm. takzhe: Galaktika, dzhet i znamenitaya chernaya dyra Akkreciruyushaya chernaya dyra s dzhetom HH 211: dzhety ot formiruyusheisya zvezdy Tri galaktiki v Drakone V rukavah NGC 1097 Zvezdy, pyl', stolby i strui v tumannosti Pelikan Blizkaya spiral'naya galaktika NGC 4945 Vse publikacii na tu zhe temu >>