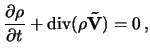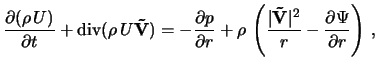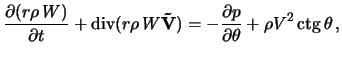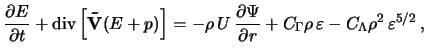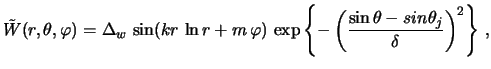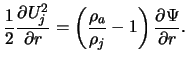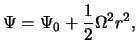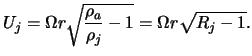Regulyarnye struktury v konusah ionizacii v okrestnosti aktivnyh yader galaktik
<< 2. Ravnovesnaya model' | Oglavlenie | 4. Rezul'taty nelineinogo modelirovaniya >>
3. Metodika chislennogo nelineinogo modelirovaniya
Ispol'zuemaya v dannoi chasti raboty stacionarnaya model' polnost'yu analogichna opisannoi vyshe. Isklyucheniya sostavlyayut konkretnye chislovye znacheniya parametrov, privedennye nami v konce dannogo razdela.
i) osnovnye uravneniya
Pri chislennom modelirovanii dinamiki vozmushenii
ispol'zovalas' sleduyushaya sistema uravnenii gidrodinamiki v divergentnoi forme
v sfericheskoi sisteme koordinat (
![]() ):
):
gde
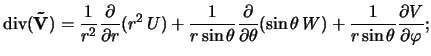
 - polnaya energiya;
- polnaya energiya;
ii) chislennaya shema i granichnye usloviya
Dlya chislennogo integrirovaniya sistemy uravnenii (14)-(18) byla realizovana
shema TVD-E [16], modificirovannaya nami dlya sfericheskoi sistemy koordinat,
s neravnomernym shagom v radial'nom napravlenii. Dlya issledovaniya dinamiki
osesimmetrichnyh vozmushenii ispol'zovalas' dvumernaya shema (![]() ) "2D" s
oblast'yu integrirovaniya (
) "2D" s
oblast'yu integrirovaniya (
![]() ;
;
![]() ),
soderzhashei
),
soderzhashei
![]() yacheek. Dlya izucheniya dinamiki
neosesimmetrichnyh vozmushenii ispol'zovalas' trehmernaya shema (
yacheek. Dlya izucheniya dinamiki
neosesimmetrichnyh vozmushenii ispol'zovalas' trehmernaya shema (
![]() ) "3D" s oblast'yu integrirovaniya (
) "3D" s oblast'yu integrirovaniya (
![]() ;
;
![]() ;
;
![]() ), soderzhashei
), soderzhashei
![]() yacheek.
yacheek.
Iz provedennogo nami lineinogo analiza sleduet, chto dlina
volny vozmushenii uvelichivaetsya lineino s radiusom, t. e.
![]() .
V sootvetstvii s etim v chislennom modelirovanii zadavalsya neravnomernyi shag
po radial'noi koordinate
.
V sootvetstvii s etim v chislennom modelirovanii zadavalsya neravnomernyi shag
po radial'noi koordinate
![]() , gde
, gde
![]() . Pri takom opredelenii
. Pri takom opredelenii ![]() kolichestvo yacheek, prihodyasheesya na dlinu volny, ostaetsya postoyannym vdol'
radiusa. V
kolichestvo yacheek, prihodyasheesya na dlinu volny, ostaetsya postoyannym vdol'
radiusa. V ![]() - i
- i ![]() -napravleniyah shag integrirovaniya zadavalsya
postoyannym, t.e.
-napravleniyah shag integrirovaniya zadavalsya
postoyannym, t.e.
![]() ,
,
![]() .
.
Chtoby izbezhat' iskazhenii v ploskosti (![]() ), obuslovlennyh
razlichnoi shemnoi skorost'yu rasprostraneniya vozmushenii v
), obuslovlennyh
razlichnoi shemnoi skorost'yu rasprostraneniya vozmushenii v ![]() - i
- i ![]() -napravleniyah,
neobhodimo zadavat' odinakovuyu dlinu yacheek
-napravleniyah,
neobhodimo zadavat' odinakovuyu dlinu yacheek
![]() i
i
![]() v etih napravleniyah sootvetstvenno, t. e.
v etih napravleniyah sootvetstvenno, t. e.
![]() ili
ili
![]() .
.
Neobhodimym usloviem raskachki neustoichivyh mod pri chislennom
modelirovanii yavlyaetsya nalichie perehodnogo sloya konechnoi tolshiny
mezhdu veshestvom strui i okruzhayushei sredoi. Perehodnyi sloi nami
zadavalsya razmerom v odnu yacheiku v ![]() -napravlenii; pri takom
opredelenii tolshina perehodnogo sloya umen'shaetsya s uvelicheniem
-napravlenii; pri takom
opredelenii tolshina perehodnogo sloya umen'shaetsya s uvelicheniem
![]() . Ravnovesnye raspredeleniya v perehodnom sloe imeyut
sleduyushii vid:
. Ravnovesnye raspredeleniya v perehodnom sloe imeyut
sleduyushii vid:
![]() ,
,
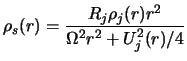 ,
,
![]() , gde indeksami
j, a i s oboznacheny velichiny, otnosyashiesya k strue, okruzhayushei
ee srede i perehodnomu sloyu mezhdu nimi sootvetstvenno.
, gde indeksami
j, a i s oboznacheny velichiny, otnosyashiesya k strue, okruzhayushei
ee srede i perehodnomu sloyu mezhdu nimi sootvetstvenno.
Nachal'noe vozmushenie ![]() -komponenty skorosti zadavalos' v sleduyushem vide:
-komponenty skorosti zadavalos' v sleduyushem vide:
gde
Ispol'zovalis' sleduyushie granichnye usloviya:
![]() v ploskosti simmetrii sistemy (
v ploskosti simmetrii sistemy (
![]() ) -
simmetrichnye granichnye usloviya
) -
simmetrichnye granichnye usloviya
![]() dlya
dlya ![]() ,
, ![]() ,
, ![]() ,
,
![]() i antisimmetrichnye
i antisimmetrichnye
![]() dlya
dlya ![]() ;
;
![]() na osi simmetrii sistemy (
na osi simmetrii sistemy (
![]() ) -
2D shema: simmetrichnye granichnye usloviya
) -
2D shema: simmetrichnye granichnye usloviya
![]() dlya
dlya ![]() ,
, ![]() ,
, ![]() i antisimmetrichnye
i antisimmetrichnye
![]() dlya
dlya ![]() ; 3D shema:
; 3D shema:
![]() ;
;
![]() pri
pri
![]() i
i
![]() -
periodicheskie usloviya
-
periodicheskie usloviya
![]() ,
,
![]() ;
;
![]() na vnutrennei (
na vnutrennei (
![]() ) i na vneshnei (
) i na vneshnei (
![]() ) po radiusu granicah -
) po radiusu granicah -
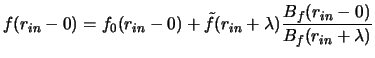 ,
,
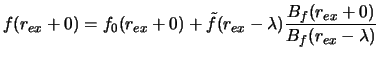 , gde
, gde ![]() - amplitudnaya funkciya
(ogibayushaya vozmushenii),
- amplitudnaya funkciya
(ogibayushaya vozmushenii), ![]() - dlina volny vozmushenii,
indeksom "0" pomecheny ravnovesnye znacheniya. V nachal'nyi moment
vremeni v sootvetstvii s rezul'tatami lineinogo analiza
amplitudnaya funkciya opredelyaetsya sleduyushim obrazom:
- dlina volny vozmushenii,
indeksom "0" pomecheny ravnovesnye znacheniya. V nachal'nyi moment
vremeni v sootvetstvii s rezul'tatami lineinogo analiza
amplitudnaya funkciya opredelyaetsya sleduyushim obrazom:
![]() . V posleduyushie momenty vremeni
. V posleduyushie momenty vremeni ![]() vychislyaetsya
posredstvom approksimacii minimumov i maksimumov vozmushenii v
raschetnyh yacheikah.
vychislyaetsya
posredstvom approksimacii minimumov i maksimumov vozmushenii v
raschetnyh yacheikah.
iii) znacheniya parametrov i sposob obezrazmerivaniya
Harakterizuyushii itensivnost' vysvechivaniya bezrazmernyi parametr ![]() opredelyaetsya otnosheniem dvuh harakternyh vremen zadachi: dinamicheskogo vremeni
opredelyaetsya otnosheniem dvuh harakternyh vremen zadachi: dinamicheskogo vremeni
![]() (vremeni rasprostraneniya vozmushenii ot
granic do osi simmetrii strui) i vremeni, za kotoroe iz-za ohlazhdeniya
vysvechivaniem energiya gaza umen'shaetsya v
(vremeni rasprostraneniya vozmushenii ot
granic do osi simmetrii strui) i vremeni, za kotoroe iz-za ohlazhdeniya
vysvechivaniem energiya gaza umen'shaetsya v ![]() raz:
raz:
![]() . Pri
. Pri
![]() vliyanie
vysvechivaniya na dinamiku vozmushenii prenebrezhimo malo. Dlya
znachenii parametra
vliyanie
vysvechivaniya na dinamiku vozmushenii prenebrezhimo malo. Dlya
znachenii parametra
![]() vysvechivanie igraet vazhnuyu rol' v evolyucii
neustoichivyh mod.
vysvechivanie igraet vazhnuyu rol' v evolyucii
neustoichivyh mod.
Raschety provodilis' dlya
![]() ,
, ![]() libo
libo ![]() ,
uglov polurastvora strui
,
uglov polurastvora strui
![]() , libo
, libo
![]() pri perepade plotnosti ot okruzhayushei sredy k strue
pri perepade plotnosti ot okruzhayushei sredy k strue ![]() , libo
, libo
![]() ; v sootvetstvii
so skazannym vyshe chislo Maha vybrosa sostavlyalo
; v sootvetstvii
so skazannym vyshe chislo Maha vybrosa sostavlyalo
![]() libo
libo
![]() .
Dlya nachal'nyh vozmushenii zadavalos'
.
Dlya nachal'nyh vozmushenii zadavalos' ![]() ,
,
![]() libo
libo
![]() (poskol'ku kachestvennyh razlichii v rezul'tatah obeih
serii ne vozniklo, dalee opisyvaetsya eksperiment s
(poskol'ku kachestvennyh razlichii v rezul'tatah obeih
serii ne vozniklo, dalee opisyvaetsya eksperiment s
![]() ).
).
Neobhodimost' zadaniya takogo sravnitel'no bol'shogo znacheniya ugla
rastvora strui diktovalas' ogranichennymi vozmozhnostyami ispol'zuemyh nami
komp'yuterov - dlya korrektnoi obrabotki vozmushenii na polurastvor strui
dolzhno prihodit'sya hotya by 10 yacheek raschetnoi oblasti, a sushestvenno
uvelichivat' ![]() my ne mogli iz-za nedostatka operativnoi pamyati i
nizkogo bystrodeistviya komp'yuterov.
my ne mogli iz-za nedostatka operativnoi pamyati i
nizkogo bystrodeistviya komp'yuterov.
Bezrazmernye granicy raschetnoi oblasti opredelyalis' znacheniyami radiusov
![]() i
i
![]() . Soglasno
skazannomu vyshe, nashe rassmotrenie provoditsya dlya radiusov, otvechayushih uchastku
tverdotel'nogo vrasheniya diska galaktiki s uglovoi skorost'yu
. Soglasno
skazannomu vyshe, nashe rassmotrenie provoditsya dlya radiusov, otvechayushih uchastku
tverdotel'nogo vrasheniya diska galaktiki s uglovoi skorost'yu
![]() km s
km s![]() kpk
kpk
![]() (chto sootvetstvuet
oblasti vnutri baldzha);
razmernoe znachenie vneshnei granicy sostavlyaet
(chto sootvetstvuet
oblasti vnutri baldzha);
razmernoe znachenie vneshnei granicy sostavlyaet
![]() kpk i, sledovatel'no, vnutrennei - v
kpk i, sledovatel'no, vnutrennei - v ![]() raz men'she:
raz men'she:
![]() pk, v zavisimosti ot
osobennostei krivyh vrasheniya real'nyh galaktik.
pk, v zavisimosti ot
osobennostei krivyh vrasheniya real'nyh galaktik.
Dlya vybora sposoba obezrazmerivaniya skorosti zamechaem, chto iz balansa davlenii v strue i v okruzhayushei ee srede sleduet, chto uravnenie (5) mozhno perepisat' v vide
Uchityvaya dalee, chto
iz (20) nahodim:
Takim obrazom, estestvenno obezrazmerivat' skorost' na
![]() .
Skorosti zvuka v strue i v okruzhayushei srede pri etom odnoznachno opredelyayutsya
bezrazmernymi parametrami
.
Skorosti zvuka v strue i v okruzhayushei srede pri etom odnoznachno opredelyayutsya
bezrazmernymi parametrami ![]() i
i ![]() . Poskol'ku dlya tipichnyh galaktik
vypolnyaetsya
. Poskol'ku dlya tipichnyh galaktik
vypolnyaetsya
![]() km/s, iz (22) sleduet, chto
struya dolzhna byt' vysokoskorostnaya (dlya vybrannogo vyshe znacheniya
km/s, iz (22) sleduet, chto
struya dolzhna byt' vysokoskorostnaya (dlya vybrannogo vyshe znacheniya ![]() ,
naprimer
,
naprimer
![]() ), nesmotrya na dozvukovoi harakter techeniya v nei
(
), nesmotrya na dozvukovoi harakter techeniya v nei
(![]() ). Eto sootvetstvuet sdelannomu vyvodu o
neobhodimosti sil'nogo razogreva veshestva strui izlucheniem yadra galaktiki.
). Eto sootvetstvuet sdelannomu vyvodu o
neobhodimosti sil'nogo razogreva veshestva strui izlucheniem yadra galaktiki.
Bezrazmernoe vremya opredelyalos' sleduyushim obrazom:
![]() . Poskol'ku dlya rassmatrivaemyh galaktik
. Poskol'ku dlya rassmatrivaemyh galaktik
![]() , to razmernoe znachenie vremeni
sostavlyaet
, to razmernoe znachenie vremeni
sostavlyaet
![]()
![]() let.
let.
Dlya obezrazmerivaniya plotnosti nami bylo vybrano znachenie
![]() g/cm
g/cm![]() , chto sootvetstvuet
koncentraciyam
, chto sootvetstvuet
koncentraciyam
![]() sm
sm![]() .
.
<< 2. Ravnovesnaya model' | Oglavlenie | 4. Rezul'taty nelineinogo modelirovaniya >>
|
Publikacii s klyuchevymi slovami:
Yadra galaktik - dzhet - Seifertovskaya galaktika
Publikacii so slovami: Yadra galaktik - dzhet - Seifertovskaya galaktika | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |