Dvizhushiesya gruppy zvezd: do i posle HIPPARCOS
<< 2. Problemy terminologii | Oglavlenie | 4. Dvizhushiesya gruppy >>
- 3.1 Metod radiantov
- 3.2 Metod Ratnatungi
- 3.3 Metod glavnyh zvezd
- 3.4 Klasternyi analiz
- 3.5 Metod "begushego" kuba (shara)
- 3.6 Neparametricheskie ocenki plotnosti
- 3.7 Veivlet-analiz
- 3.8 Metod "spagetti"
3. Kak iskat' dvizhushiesya gruppy?
Metody vydeleniya gruppirovok zvezd, kotorye obladayut obshim dvizheniem v prostranstve, mozhno razdelit' na tri tipa v zavisimosti ot teh nablyudatel'nyh dannyh, kotorye ispol'zuyutsya:
- metody, v kotoryh ispol'zuetsya tol'ko informaciya o polozheniyah zvezd na nebe i ih sobstvennyh dvizheniyah s vozmozhnym privlecheniem dannyh o luchevyh skorostyah;
- metody, v kotoryh takzhe ispol'zuyutsya parallaksy zvezd;
- metody, osnovannye na dannyh o prostranstvennyh skorostyah.
Rassmotrim bolee podrobno neskol'ko metodov poiska dvizhushihsya skoplenii.
3.1 Metod radiantov
Dlya opredeleniya radiantov i antiradiantov vozmozhnyh dvizhushihsya grupp rassmatrivaetsya sovokupnost' vektorov sobstvennyh dvizhenii zvezd. Tochki shodimosti sobstvennyh dvizhenii priblizhenno opredelyayutsya graficheski. Zatem polozheniya etih tochek mozhno utochnit', naprimer, minimiziruya summu kvadratov rasstoyanii ot tochki predpolagaemogo radianta do bol'shih krugov, provedennyh vdol' vektorov sobstvennyh dvizhenii zvezd.
V metode radiantov voznikaet problema otbora chlenov gruppy. Chasto v kachestve takovyh berut zvezdy, dlya kotoryh vypolnyaetsya neravenstvo
 |
(1) |
gde 
- pozicionnyi ugol vektora sobstvennogo
dvizheniya zvezdy;
- pozicionnyi ugol napravleniya
so zvezdy na radiant; 
- uglovoe rasstoyanie mezhdu
zvezdoi i radiantom; 
- parametr.
Zametim, chto metod radiantov imeet elementy sub'ektivizma,
svyazannye s predvaritel'nym vyborom radianta i parametra .
Dlya otbora chlenov gruppy mozhno privlech' takzhe informaciyu o luchevyh skorostyah zvezd.
3.2 Metod Ratnatungi
V etom metode [6] ispol'zuetsya informaciya o luchevyh skorostyah zvezd i pozicionnyh uglah vektorov sobstvennyh dvizhenii. Avtor perehodit ot etih parametrov k dvum parametram, kotorye ravny nulyu dlya chlenov dvizhusheisya gruppy, a imenno luchevaya skorost' ispravlyaetsya za dvizhenie gruppy otnositel'no Solnca, a pozicionnyi ugol sobstvennogo dvizheniya privoditsya v sistemu otscheta, v kotoroi polyusa sovpadayut s tochkami radianta i antiradianta. Pri etom vvoditsya mnozhitel', ravnyi sinusu uglovogo rasstoyaniya mezhdu zvezdoi i apeksom (antiradiantom) gruppy.
Zametim, chto dlya primeneniya metoda Ratnatungi neobhodima
predvaritel'naya informaciya o dvizhenii gruppy. Etot
metod mozhno ispol'zovat' dlya ocenki stepeni kompaktnosti
dvizhusheisya gruppy v prostranstve skorostei.
3.3 Metod glavnyh zvezd
V etom metode [7,8] ispol'zuyutsya dannye o prostranstvennyh skorostyah zvezd. V prostranstve skorostei vydelyayutsya zvezdy - centry sgushenii, vokrug kotoryh imeyutsya lokal'nye maksimumy plotnosti. Dlya etogo vokrug kazhdoi zvezdy stroitsya sfera opredelennogo radiusa i podschityvaetsya chislo zvezd-sputnikov, okazavshihsya vnutri etoi sfery. Nahodyatsya zvezdy, kotorye imeyut maksimal'noe chislo sputnikov po sravneniyu s ih sputnikami. Eti zvezdy - centry lokal'nyh sgushenii - budem nazyvat' glavnymi zvezdami.
Odna iz problem etogo metoda - vybor radiusa sfery. Slishkom
bol'shoe znachenie radiusa umen'shaet razreshenie metoda, slishkom
malyi radius ne pozvolyaet vydelyat' gruppy iz-za oshibok nablyudenii
i real'noi dispersii skorostei v gruppe zvezd. Razumnyi kompromiss
km/s.
3.4 Klasternyi analiz
Metody klasternogo analiza ispol'zuyutsya vo mnogih oblastyah nauki dlya poiska sgushenii ob'ektov. Ideya etogo podhoda sostoit v predstavlenii raspredeleniya zvezd v prostranstve skorostei v vide ierarhicheskogo dereva (sm., naprimer, [8,9]).
List'ya dereva - otdel'nye zvezdy. List'ya ob'edinyayutsya v vetvi-klastery po opredelennomu zakonu maksimal'noi blizosti. Zatem kazhdyi klaster, sostoyashii iz dvuh i bolee zvezd, rassmatrivaetsya kak otdel'nyi ob'ekt, i procedura klasterizacii povtoryaetsya snova.
Problemy klasternogo analiza - vybor rasstoyaniya mezhdu ob'ektami i vybor momenta "obrezaniya" v procedure klasterizacii.
3.5 Metod "begushego" kuba (shara)
Etot metod sostoit v skanirovanii prostranstva skorostei kubom ili sharom nebol'shogo ob'ema. Podschityvaetsya chislo zvezd v predelah etogo kuba ili shara. Poluchennoe chislo sravnivaetsya s chislom zvezd, ozhidaemym pri sluchainom raspredelenii. Esli nablyudaemoe chislo znachimo prevoshodit ozhidaemoe, to mozhno predpolozhit', chto v etom kube ili share raspolagaetsya dvizhushayasya gruppa ili chast' gruppy.
Problemu sostavlyaet vybor razmera kuba ili shara, a takzhe vozmozhnost' ob'edineniya neskol'kih sosednih kubov ili sharov s povyshennoi koncentraciei zvezd v odnu gruppu.
3.6 Neparametricheskie ocenki plotnosti
Pri takom podhode
[10-11]
raspredelenie ostatochnyh skorostei
zvezd v tochke
ocenivaetsya s pomosh'yu "yadernoi"
funkcii vida
 |
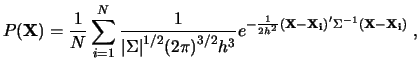(2) |
gde 
- chislo zvezd v rassmatrivaemoi vyborke;
- vektor
prostranstvennoi skorosti 
-i zvezdy; 
- parametr
sglazhivaniya (ili shirina okna); 
- kovariacionnaya
matrica.
Predpolagaetsya, chto funkciya
 |
(3) |
gde pervoe slagaemoe opredelyaet vklad zvezd polya, a vtoroe - vklad zvezd gruppy. Dlya zvezd polya mozhno predpolozhit' ellipsoidal'noe raspredelenie, parametry kotorogo (srednie i elementy kovariacionnoi matricy) opredelyayutsya iz nablyudenii.
Chleny grupp vydelyayutsya po prevysheniyu funkciei (2) nekotorogo porogovogo
znacheniya 
, kotoroe zavisit ot prinyatogo urovnya znachimosti.
Procedura formirovaniya grupp zakanchivaetsya, esli bol'she ne nahoditsya
novyh chlenov.
3.7 Veivlet-analiz
Preobrazovanie "malen'koi volny", ili veivlet-analiz, v poslednee desyatiletie nashel shirokoe primenenie prakticheski vo vseh oblastyah estestvoznaniya, gde trebuetsya vydelit' te ili inye struktury.
Pri issledovanii prostranstva skorostei zvezd primenyaetsya
trehmernyi veivlet-analiz [12,13]. Esli my rassmotrim
raspredelenie zvezd v prostranstve skorostei kak trehmernyi signal
, to my mozhem predstavit' preobrazovanie
"malen'koi volny" kak svertku etogo raspredeleniya s nekotoroi
funkciei
. Eta funkciya vybiraetsya takim
obrazom, chtoby ona dostatochno bystro spadala pri udalenii ot
interesuyushei nas tochki. Koefficienty veivleta imeyut bol'shie
polozhitel'nye velichiny v oblastyah povyshennoi plotnosti i bol'shie
po modulyu, no otricatel'nye znacheniya - v mestah ponizhennoi
plotnosti zvezd.
Dlya togo chtoby otdelit' veroyatno nesluchainye sgusheniya zvezd ot sluchainyh fluktuacii, neobhodimo vvesti nekotorye porogovye znacheniya veivlet-koefficientov, kotorye v obshem sluchae zavisyat ot masshtaba i polozheniya tochki v prostranstve skorostei. Porogovye znacheniya opredelyayutsya iz ocenok urovnya shuma, porozhdennogo pri tom zhe samom masshtabe ravnomerno sluchainym signalom. Prichem krupnomasshtabnye harakteristiki sluchainogo signala sovpadayut s tak nazyvaemymi gross-harakteristikami nablyudaemogo raspredeleniya.
3.8 Metod "spagetti"
V etom metode [14] ispol'zuetsya tol'ko astrometricheskaya informaciya: polozheniya zvezd na nebe, ih parallaksy i sobstvennye dvizheniya. Kazhdoi zvezde stavitsya v sootvetstvie nekotoryi cilindr ("makaronina") v prostranstve skorostei. Etot cilindr ortogonalen vektoru tangencial'noi skorosti zvezdy i parallelen luchu zreniya. Tolshina cilindra opredelyaetsya oshibkami sobstvennogo dvizheniya i parallaksa zvezdy.
Spagetti, sootvetstvuyushie zvezdam odnogo i togo zhe dvizhushegosya skopleniya, peresekayutsya v odnoi i toi zhe tochke - centroide skopleniya.
Takim obrazom, vydelyaya sgusheniya etih tochek v prostranstve skorostei, my nahodim veroyatnye centroidy dvizhushihsya grupp zvezd.
<< 2. Problemy terminologii | Oglavlenie | 4. Dvizhushiesya gruppy >>
|
Publikacii s klyuchevymi slovami:
gruppy zvezd - Sobstvennoe dvizhenie - astrometriya - ISZ Giparhos - Hipparcos
Publikacii so slovami: gruppy zvezd - Sobstvennoe dvizhenie - astrometriya - ISZ Giparhos - Hipparcos | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |
