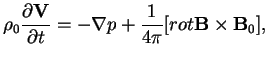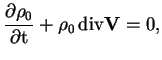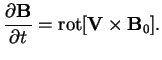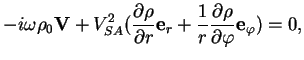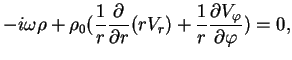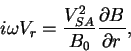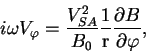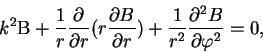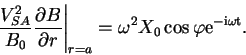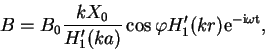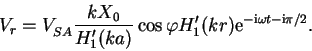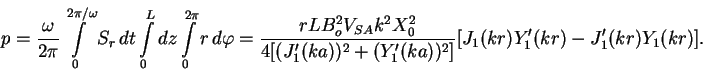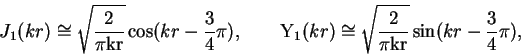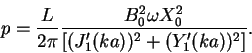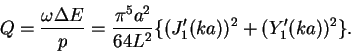Radiacionnoe zatuhanie kolebanii koronal'nyh petel'
<< 2. Perioda svobodnyh kolebanii | Oglavlenie | 4. Sila reakcii izlucheniya >>
3. Radiacionnoe zatuhanie kolebanii petli vo vneshnem magnitnom pole
Issleduem vozbuzhdenie MGD-voln slaboiskrivlennoi koronal'noi petlei, koleblyusheisya vo vneshnem magnitnom pole. Dlya etogo rasschitaem potok volnovoi energii, unosimoi etimi volnami s edinicy poverhnosti cilindra, sovershayushego vo vneshnem pole poperechnye kolebaniya zadannoi amplitudy.
Rassmotrim kruglyi pryamoi cilindr dliny L, radiusa poperechnogo secheniya
a, zapolnennyi odnorodnym magnitnym polem i ideal'no
provodyashei plazmoi. Magnitnoe pole V vo vneshnei srede takzhe
schitaem soosnym cilindru i odnorodnym, a plazmu plotnosti ![]() -
ideal'no provodyashei. Pust' cilindr bez izmeneniya svoei formy i razmera
sovershaet v napravlenii osi h poperechnye garmonicheskie kolebaniya
(ris. 2,a), t.e. ego os' menyaet polozhenie so vremenem po zakonu
h = H(t),
gde:
-
ideal'no provodyashei. Pust' cilindr bez izmeneniya svoei formy i razmera
sovershaet v napravlenii osi h poperechnye garmonicheskie kolebaniya
(ris. 2,a), t.e. ego os' menyaet polozhenie so vremenem po zakonu
h = H(t),
gde:
Budem dlya prostoty raschetov schitat' kolebaniya dostatochno malymi:
![]() , nesmotrya na to, chto amplituda real'no
nablyudaemyh kolebanii petel'
, nesmotrya na to, chto amplituda real'no
nablyudaemyh kolebanii petel' ![]() (v srednem okolo 4 tysyach km)
prevyshaet
(v srednem okolo 4 tysyach km)
prevyshaet
![]() , kotoroe, po dannym TRACE sostavlyaet, kak otmechalos' vo Vvedenii, 1-2
tysyachi km, a po dannym apparata SOHO - 3-4 tysyachi km (sm. obsuzhdenie v
[1]). V pol'zu prinyatogo nami podhoda imeyutsya sleduyushie argumenty:
vo-pervyh, priblizhenie malosti poperechnyh kolebanii mozhet privesti tol'ko
k nedoocenke izuchaemogo effekta radiacionnogo zatuhaniya. Esli uzhe v etom
priblizhenii udaetsya reshit' problemu, to, ochevidno, net neobhodimosti
stroit' znachitel'no bolee slozhnuyu teoriyu nelineinyh kolebanii.
Vo-vtoryh, neobhodimo uchest', chto nablyudeniyami fiksiruetsya tol'ko
central'naya, naibolee plotnaya i goryachaya chast' koronal'noi magnitnoi petli.
Radius ee effektivnogo secheniya
, kotoroe, po dannym TRACE sostavlyaet, kak otmechalos' vo Vvedenii, 1-2
tysyachi km, a po dannym apparata SOHO - 3-4 tysyachi km (sm. obsuzhdenie v
[1]). V pol'zu prinyatogo nami podhoda imeyutsya sleduyushie argumenty:
vo-pervyh, priblizhenie malosti poperechnyh kolebanii mozhet privesti tol'ko
k nedoocenke izuchaemogo effekta radiacionnogo zatuhaniya. Esli uzhe v etom
priblizhenii udaetsya reshit' problemu, to, ochevidno, net neobhodimosti
stroit' znachitel'no bolee slozhnuyu teoriyu nelineinyh kolebanii.
Vo-vtoryh, neobhodimo uchest', chto nablyudeniyami fiksiruetsya tol'ko
central'naya, naibolee plotnaya i goryachaya chast' koronal'noi magnitnoi petli.
Radius ee effektivnogo secheniya
![]() , ispol'zuemyi v
MGD-modelyah, zavedomo prevyshaet
, ispol'zuemyi v
MGD-modelyah, zavedomo prevyshaet
![]() .
(V rabote [1] na str. 890 dlya chislennyh
ocenok prinimalos'
.
(V rabote [1] na str. 890 dlya chislennyh
ocenok prinimalos'
![]() = 3600 km).
= 3600 km).
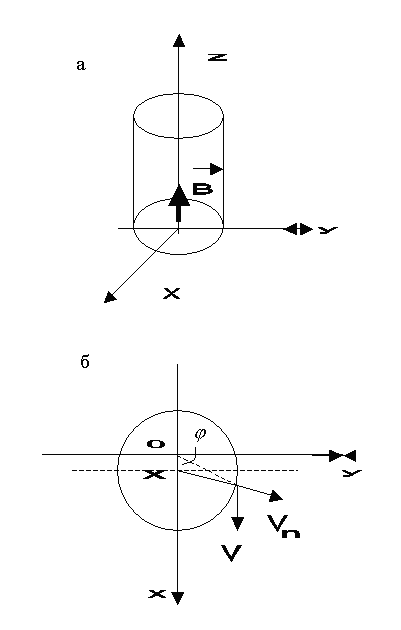 |
Ris. 2. a). Cilindr, sovershayushii poperechnye kolebaniya vdol' osi H. b). Vid sverhu. Priblizhenie malyh kolebanii |
Takim obrazom, v real'noi situacii, vidimo,
![]() , no my vybiraem priblizhenie malyh kolebanii, kak
vpolne dostatochnoe dlya opisaniya osnovnogo effekta.
, no my vybiraem priblizhenie malyh kolebanii, kak
vpolne dostatochnoe dlya opisaniya osnovnogo effekta.
V ukazannom priblizhenii dlya normal'noi k poverhnosti cilindra sostavlyayushei skorosti mozhno prinyat' (ris. 2,b):
Rassmotrim volny, vozbuzhdaemye cilindrom vo vneshnei srede. Linearizovannye uravneniya ideal'noi MGD dlya odnorodnoi plazmy imeyut vid:
Zdes' ![]() ,
, ![]() ,
, ![]() ,
,
![]() - nevozmushennye
parametry sredy,
- nevozmushennye
parametry sredy, ![]() ,
, ![]() ,
, ![]() ,
, ![]() - vozmusheniya. Budem
rassmatrivat' reshenie vida:
- vozmusheniya. Budem
rassmatrivat' reshenie vida:
V etom sluchae sistema (6)-(8) daet:
Otsyuda sleduet:
gde ispol'zovano obychnoe oboznachenie:
Obshee reshenie uravneniya (16) mozhno zapisat' cherez funkcii Gankelya sleduyushim obrazom:
Konstantu S naidem iz granichnogo usloviya nepreryvnosti normal'noi sostavlyayushei skorosti na poverhnosti cilindra: pri
Otsyuda poluchaem:
![]() . Sledovatel'no, vneshnee
reshenie kraevoi zadachi imeet vid:
. Sledovatel'no, vneshnee
reshenie kraevoi zadachi imeet vid:
(Dlya polnoty issledovaniya mozhno bylo by zapisat' i vnutrennee reshenie, opredeliv ego konstanty cherez usloviya nepreryvnosti normal'noi skorosti i polnogo davleniya na granice. No, kak uzhe otmechalos', dlya resheniya dannoi zadachi dlya nas osnovnoi interes predstavlyaet imenno vneshnee reshenie, opredelyayushee effekt radiacionnogo zatuhaniya).
Potok volnovoi energii opredelyaetsya vektorom Umova-Poitinga:
Ispol'zuya poslednyuyu formulu i vydelyaya v reshenii (21) , (22) real'nye chasti, mozhno rasschitat' usrednennyi po periodu kolebanii potok volnovoi energii, unosimoi s poverhnosti cilindra proizvol'nogo radiusa r i dliny L v edinicu vremeni. Opuskaya gromozdkie promezhutochnye vykladki, zapishem okonchatel'nyi rezul'tat:
Vychisliv opredelitel' Vronskogo dlya uravneniya Besselya, mozhno pokazat', chto
Otsyuda vidno, chto potok energii r ne zavisit ot rasstoyaniya ![]() ot
osi cilindra i opredelyaetsya kvadratom amplitudy kolebanii.
ot
osi cilindra i opredelyaetsya kvadratom amplitudy kolebanii.
Uchityvaya asimptotiku funkcii Besselya pervogo i vtorogo roda:
vyrazhenie dlya potoka volnovoi energii udobno predstavit' v forme:
Podcherknem, chto v eto vyrazhenie vhodyat tol'ko dostupnye dlya izmerenii velichiny: geometricheskie razmery petli, napryazhennost' magnitnogo polya, chastota i amplituda kolebanii.
V pervom razdele bylo polucheno vyrazhenie dlya energii vozmusheniya magnitnoi
petli:
![]() ,
sootvetstvuyushei srednemu po petle otkloneniyu
,
sootvetstvuyushei srednemu po petle otkloneniyu
![]() v nekotoryi moment
vremeni. Razdeliv ego na potok energii r i period kolebanii
T, my
poluchim chislo, pokazyvayushee za kakoe kolichestvo periodov energiya sistemy,
zapasennaya pri pervonachal'nom vozmushenii, budet rasseyana v rezul'tate
izlucheniya voln v okruzhayushee prostranstvo. Umnozhaya eto chislo na 2
v nekotoryi moment
vremeni. Razdeliv ego na potok energii r i period kolebanii
T, my
poluchim chislo, pokazyvayushee za kakoe kolichestvo periodov energiya sistemy,
zapasennaya pri pervonachal'nom vozmushenii, budet rasseyana v rezul'tate
izlucheniya voln v okruzhayushee prostranstvo. Umnozhaya eto chislo na 2![]() ,
naidem dobrotnost' kolebatel'noi sistemy, t.e. vyrazim tu zhe velichinu v
radianah:
,
naidem dobrotnost' kolebatel'noi sistemy, t.e. vyrazim tu zhe velichinu v
radianah:
Otmetim, chto poskol'ku r i ![]() zavisyat odinakovym
(kvadratichnym) obrazom ot amplitudy smesheniya
zavisyat odinakovym
(kvadratichnym) obrazom ot amplitudy smesheniya
![]() ,
to v (29) eta velichina
sokrashaetsya. Argument Besselevyh funkcii v (29)
v dannom sluchae dostatochno
mal:
,
to v (29) eta velichina
sokrashaetsya. Argument Besselevyh funkcii v (29)
v dannom sluchae dostatochno
mal: ![]() . Nizhe dlya chislennyh ocenok my budem prinimat'
sleduyushie velichiny:
. Nizhe dlya chislennyh ocenok my budem prinimat'
sleduyushie velichiny:
![]() sm/s (soglasno ocenke,
privedennoi v [1]);
sm/s (soglasno ocenke,
privedennoi v [1]);
![]() cm
(v soglasii s [1] i v
sootvetstvii s izlozhennymi vyshe soobrazheniyami, o tom, chto real'nyi radius
magnitnoi trubki zavedomo prevyshaet ego nablyudaemuyu velichinu); dlya chastoty
kolebanii i dliny trubki primem dannye dlya petli, rassmotrennoi v [4]: L =
130 000 km, chastota
cm
(v soglasii s [1] i v
sootvetstvii s izlozhennymi vyshe soobrazheniyami, o tom, chto real'nyi radius
magnitnoi trubki zavedomo prevyshaet ego nablyudaemuyu velichinu); dlya chastoty
kolebanii i dliny trubki primem dannye dlya petli, rassmotrennoi v [4]: L =
130 000 km, chastota
![]() Gc, chto sootvetstvuet
periodu kolebanii T = 256,4 s. V etom sluchae poluchaetsya:
Gc, chto sootvetstvuet
periodu kolebanii T = 256,4 s. V etom sluchae poluchaetsya:
![]() .
Uchityvaya rekurrentnye sootnosheniya
.
Uchityvaya rekurrentnye sootnosheniya
Podstanovka v etu formulu privedennyh vyshe chislennyh velichin daet Q ![]() 8.756.
8.756.
<< 2. Perioda svobodnyh kolebanii | Oglavlenie | 4. Sila reakcii izlucheniya >>
|
Publikacii s klyuchevymi slovami:
Solnechnaya korona - magnitnoe pole Solnca - magnitnaya gidrodinamika - Solnce
Publikacii so slovami: Solnechnaya korona - magnitnoe pole Solnca - magnitnaya gidrodinamika - Solnce | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |