Astronet > Variacionnye principy v fizike

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Variacionnye principy v fizike

E. D. Trifonov

Rossiiskii gosudarstvennyi pedagogicheskii universitet im. A.I. Gercena, Sankt-Peterburg

Mnogie zakony fiziki mogut byt' vyvedeny iz utverzhdeniya, chto dlya istinnogo razvitiya issleduemogo processa opredelennaya harakteristicheskaya velichina dostigaet minimal'nogo (v bolee obshem sluchae ekstremal'nogo) znacheniya po sravneniyu s ee znacheniyami dlya nekotoryh drugih vozmozhnyh techenii etogo processa. Chtoby matematicheski sformulirovat' eto utverzhdenie, neobhodimo vvesti v rassmotrenie uravneniya, opisyvayushie dannyi process, i s pomosh'yu izmeneniya (variacii) ih formy dobit'sya dostizheniya ekstremal'nogo znacheniya vychislyaemoi harakteristicheskoi velichiny. Te uravneniya, pri kotoryh eto ekstremal'noe znachenie dostigaetsya, i vyrazhayut istinnye zakony izuchaemogo yavleniya. V takom sluchae dannoe utverzhdenie prinimayut za ishodnoe i nazyvayut variacionnym nachalom ili variacionnym principom.

Obychnoe izlozhenie mehaniki (naprimer, kak v shkol'nom kurse) osnovyvaetsya na treh zakonah N'yutona. Kak izvestno, I. N'yuton vnes osobenno znachitel'nyi vklad v razvitie mehaniki. V svoem trude "Matematicheskie nachala natural'noi filosofii" (1687) [1] on reshil mnozhestvo slozhnyh zadach o dvizhenii material'noi tochki v pole central'nyh sil i etim konstruktivno podtverdil pravil'nost' zakona vsemirnogo tyagoteniya. Chto kasaetsya vtorogo zakona N'yutona, to, ocenivaya ego znachenie, A. Einshtein nazyval ego glavnym zakonom ne tol'ko mehaniki, no i vsei fiziki. N'yuton (naryadu s G.V. Leibnicem) byl sozdatelem differencial'nogo i integral'nogo ischislenii, odnako pri reshenii mehanicheskih zadach on pochti ne pol'zovalsya etim matematicheskim metodom. On primenyal geometricheskii metod. V upomyanutoi vyshe knige mnogo chertezhei, a stil' resheniya zadach napominaet dokazatel'stvo geometricheskih teorem.

Drugoe napravlenie v mehanike vozniklo posle rabot L. Eilera, v kotoryh byl ispol'zovan metod differencial'nogo i integral'nogo ischislenii v forme, predlozhennoi Leibnicem. Osoboe razvitie eto napravlenie poluchilo v trudah Zh. Lagranzha. Lagranzh gordilsya tem, chto v ego knige "Analiticheskaya mehanika" (1788) net ni odnogo risunka ili chertezha. Imenno s primeneniem analiticheskih metodov v mehanike svyazany intensivnoe razvitie i primenenie variacionnyh principov. Sam termin "variacionnyi princip" byl vpervye predlozhen v rabote Eilera. Odnako, poskol'ku differencial'noe i integral'noe ischisleniya lezhat na granice shkol'nyh znanii po matematike, my ne budem zloupotreblyat' imi i postaraemsya poyasnit' fizicheskuyu ideyu variacionnyh principov s pomosh'yu elementarnyh sredstv, dostupnyh shkol'nikam. Eto kak raz i budet sostavlyat' metodicheskuyu osobennost' nashego izlozheniya. Navernoe, etot prostoi vzglyad na dostatochno slozhnuyu problemu okazhetsya poleznym i dlya teh, kto budet izuchat' eti voprosy na bolee ser'eznom urovne. My takzhe sovetuem zainteresovannomu chitatelyu poznakomit'sya so stat'ei [2], posvyashennoi izlozheniyu optiko-mehanicheskoi analogii.

V nashi dni ispolnyaetsya 300 let s togo momenta, kogda byli opublikovany pervye soobsheniya o variacionnom principe v mehanike. V korotkom pis'me na polstranicy, opublikovannom v iyun'skom nomere nemeckogo nauchnogo zhurnala "Uchenye trudy" ("Acta Eruditorum") za 1696 god (sm. [3]), Iogann Bernulli postavil sleduyushuyu zadachu: "V vertikal'noi ploskosti dany dve tochki A i V. Opredelit' put', spuskayas' po kotoromu pod vliyaniem sobstvennoi tyazhesti, telo, nachav dvigat'sya iz tochki A, doidet do tochki V za kratchaishee vremya". V konce pis'ma govorilos', chto eta krivaya horosho izvestna v geometrii i chto esli po istechenii tekushego goda nikto ne opublikuet reshenie, to eto sdelaet sam avtor. V etot srok otkliknulsya tol'ko Leibnic. Soobshaya, chto uzhe reshil postavlennuyu zadachu, on predlozhil prodlit' konkurs do Pashi sleduyushego goda. I vot v maiskom nomere togo zhe zhurnala za 1697 god byli opublikovany resheniya etoi zadachi, poluchennye Leibnicem, Yakobom Bernulli (bratom I. Bernulli), G. Lopitalem i samim Iogannom Bernulli. V maiskom zhe nomere angliiskogo zhurnala "Filosofskie trudy" ("Philosophical Transactions") bylo pomesheno reshenie N'yutona bez podpisi. No I. Bernulli opredelil avtora. Istoriya sohranila ego slova: "Ya uznal l'va po ego kogtyam".

Kak budet pokazano nizhe, ideya variacionnyh principov v mehanike byla iniciirovana variacionnym principom v optike - principom Ferma.

Variacionnyi princip geometricheskoi optiki - princip Ferma

Variacionnyi princip geometricheskoi optiki byl predlozhen P'erom Ferma (1601-1665) neskol'ko ranee opisannyh vyshe sobytii, a imenno v 1662 godu: Esli dve tochki nahodyatsya v razlichnyh prozrachnyh (odnorodnyh) sredah, to luch sveta, chtoby proiti ot odnoi tochki k drugoi, prelomlyaetsya u ploskoi poverhnosti, po kotoroi soprikasayutsya obe sredy, takim obrazom, chto upotreblyaet vozmozhno men'shee vremya, sovershenno tak zhe, kak eto proishodit pri otrazhenii ot ploskoi poverhnosti. Hotya sam Ferma ishodil iz dovol'no obshego postulata - priroda deistvuet naibolee legkimi i dostupnymi putyami, - ego stat'ya nosila vpolne konstruktivnyi harakter (sm.[3]). On dokazal, chto princip naimen'shego vremeni yavlyaetsya sledstviem zakona prelomleniya.

Vyshe my priveli formulirovku principa Ferma, dannuyu Hristianom Gyuigensom (1629-1695), sovremennikom Ferma, v ego znamenitom "Traktate o svete" (1678) [4]. My vosproizvedem zdes' takzhe pochti doslovno prinadlezhashee emu dokazatel'stvo principa Ferma, obladayushee bol'shei prostotoi po sravneniyu s dokazatel'stvom samogo Ferma.

Tak zhe kak i Ferma, Gyuigens schital, chto v plotnoi srede svet rasprostranyaetsya s men'shei skorost'yu, chem v vakuume. Pust' KF - ploskost', razdelyayushaya dve sredy (ris. 1), i tochka A nahoditsya v menee plotnoi srede (naprimer, v vozduhe), a tochka C - v bolee plotnoi srede (naprimer, v vode). Pust' luch prohodit iz tochki A cherez tochku B, lezhashuyu na granice, v tochku C v sootvetstvii s zakonom prelomleniya

$$\frac{\sin\alpha_1}{\sin\alpha_2}=\frac{n_2}{n_1}=\frac{c_1}{c_2},$ (1)$

gde n₁, c₁, n₂, c₂ - pokazateli prelomleniya i skorosti rasprostraneniya sveta v verhnei i nizhnei sredah sootvetstvenno. Po predpolozheniyu, n₁<n₂, c₁>c₂.

Trebuetsya dokazat', chto vremya prohozhdeniya sveta po takomu luchu samoe korotkoe po sravneniyu s vremenem prohozhdeniya po lyubomu drugomu prelomlennomu luchu. Primenim dokazatel'stvo ot protivnogo. Dopustim, chto svet proshel po drugomu luchu AFC, tak chto tochka F otstoit ot tochki A dal'she, chem tochka B. Provedem pryamuyu FO', parallel'nuyu AB, i postroim perpendikulyary AO i BH k etim pryamym. Opustim takzhe perpendikulyar FG na pryamuyu BC. Iz togo, chto $\angle HBF$ raven $\angle PBA$ , a $\angle BFG$ raven $\angle QBC$ (kak ugly s sootvetstvenno ortogonal'nymi storonami), sleduet, chto

$$\frac{HF}{BG}=\frac{\sin\alpha_1}{\sin\alpha_2}.$ (2)$

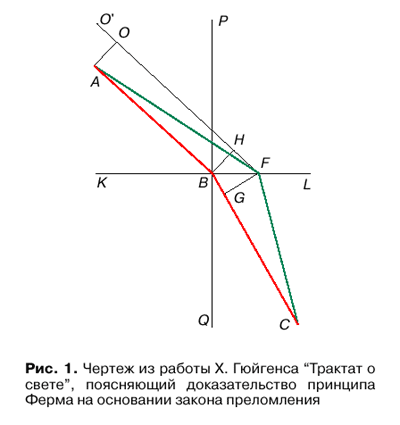
Poetomu, soglasno (1), vremya rasprostraneniya sveta po otrezku HF ravno vremeni rasprostraneniya po otrezku BG:

$\frac{HF}{c_1}=\frac{BG}{c_2}$

Takim obrazom, vremya prohozhdeniya sveta po luchu OF bylo by ravno vremeni prohozhdeniya sveta po puti ABG. Dalee ochevidno, chto tak kak gipotenuza FC bol'she kateta GC, to vremya prohozhdeniya po puti OFC bol'she, chem po puti ABC. Nakonec, poskol'ku gipotenuza AF bol'she kateta OF, to vremya prohozhdeniya sveta po puti AFC bol'she vremeni prohozhdeniya sveta po puti OFC i tem bolee po puti ABC. K analogichnomu zaklyucheniyu mozhno priiti i v sluchae, kogda tochka F lezhit levee tochki B. Takim obrazom, vremya prohozhdeniya sveta po ABC samoe korotkoe iz vozmozhnyh, chto i trebovalos' dokazat'.

Interesno, chto dokazatel'stvu Gyuigensa zakona prelomleniya na osnovanii ego gipotezy o volnovoi prirode sveta (kotoroe privoditsya v shkol'nom kurse fiziki) predshestvovalo rassuzhdenie patera Men'yana "O soldatskom fronte" (1648) (sm. [5]). Ego ispol'zoval Isaak Barrou (1631-1667) v svoih "Lekciyah po matematike i optike" (1668), v podgotovke k izdaniyu kotoryh uchastvoval Isaak N'yuton (1643-1727). (N'yuton byl uchenikom i preemnikom Barrou po Lukasovskoi kafedre v Kembridzhskom universitete.) Eti rassuzhdeniya ochen' prosty i naglyadny. Oni svodyatsya k tomu, chto pri perehode iz odnoi sredy v druguyu svetovoi front menyaet svoe napravlenie tak zhe, kak menyaet napravlenie sherenga soldat, kogda lug, po kotoromu idut soldaty, pregrazhdaetsya pashnei i granica mezhdu pashnei i lugom prohodit pod uglom k sherenge. Skorost' dvizheniya soldat po pashne men'she, chem po lugu. Dlya sohraneniya stroya soldaty dolzhny marshirovat' po parallel'nym liniyam kak pri dvizhenii po lugu, tak i po pashne. Risunok, illyustriruyushii takoe dvizhenie soldatskogo fronta, analogichen tomu, kotoryi ispol'zoval Gyuigens dlya ob'yasneniya izmeneniya volnovogo fronta pri prelomlenii i kotoryi teper' vosproizvoditsya vo vseh uchebnikah. Ochevidno, chto front soldat bystree vsego peresechet lyuboe zamechennoe mesto na pashne, esli napravlenie sherengi budet podchinyat'sya zakonu prelomleniya (1). Takim obrazom, v etih rassuzhdeniyah fakticheski soderzhalos' dokazatel'stvo zakona prelomleniya na osnovanii principa Ferma.

Princip Ferma spravedliv dlya lyuboi neodnorodnoi opticheskoi sredy s nepreryvno izmenyayushimsya pokazatelem prelomleniya. Zdes' tol'ko sleduet sdelat' sushestvennuyu ogovorku: v neodnorodnoi opticheskoi srede dve tochki mogut byt' soedineny neskol'kimi luchami (primerom mozhet sluzhit' hod luchei pri vozniknovenii nizhnego mirazha) (sm. [2]). Poetomu trebuetsya utochnenie formulirovki principa Ferma: vremya rasprostraneniya sveta vdol' lucha mezhdu dvumya tochkami neodnorodnoi opticheskoi sredy s nepreryvno izmenyayushimsya pokazatelem prelomleniya minimal'no po sravneniyu s vremenem rasprostraneniya sveta vdol' lyuboi beskonechno blizkoi traektorii, soedinyayushei eti zhe tochki. Po povodu drugih utochnenii formulirovki principa Ferma my vynuzhdeny otoslat' chitatelya k bolee detal'nomu izlozheniyu etogo voprosa [6].

Zadacha o brahistohrone

Teper' rasskazhem bolee podrobno o tom samom variacionnom principe, kotoryi byl predlozhen Iogannom Bernulli (1667-1748). Postavlennaya im zadacha poluchila nazvanie zadachi o brahistohrone, to est' o linii naibystreishego spuska. Predpolagaetsya, chto material'naya tochka nahoditsya v odnorodnom pole tyazhesti i mozhet skatyvat'sya vniz po nekotoroi traektorii (kak businka, nanizannaya na provoloku opredelennoi formy). Treniem pri etom prenebregayut, a nachal'naya skorost' material'noi tochki ravna nulyu. Otvet, poluchennyi I. Bernulli: etoi krivoi yavlyaetsya cikloida - krivaya, kotoruyu opisyvaet tochka na obode kolesa pri ego kachenii.

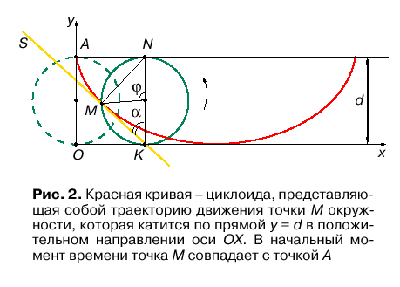
Rassmotrim odno vazhnoe dlya dal'neishego svoistvo cikloidy. Pust' zadana okruzhnost' diametra d, kotoraya katitsya po pryamoi y = d v polozhitel'nom napravlenii osi OX, kak eto pokazano na ris. 2.

Pust' tochka M okruzhnosti v nachal'nyi moment vremeni imela koordinaty x = 0, y = d. K momentu vremeni t okruzhnost' povernulas' na ugol $\phi$ , i tochkoi kasaniya okruzhnosti osi OX yavlyaetsya tochka N. Tochka N imeet nulevuyu mgnovennuyu skorost', i, kak govoryat, cherez nee prohodit mgnovennaya os' vrasheniya. Poetomu tochka M v dannyi moment dvizhetsya po okruzhnosti radiusa MN, a kasatel'naya k cikloide v tochke M perpendikulyarna k mgnovennomu radiusu vrasheniya MN.

Uchityvaya eto, mozhno bez bol'shogo truda opredelit', chto ugol $\alpha$ , kotoryi kasatel'naya SMK obrazuet s os'yu OY, raven $\phi/2$ . Ordinatu y tochki M mozhno predstavit' v vide

$$y=\frac{d}{2}+\frac{d}{2}\cos\phi.$ (3)$

Otsyuda s pomosh'yu elementarnyh trigonometricheskih formul poluchaem uravnenie, svyazyvayushee ordinatu tochki cikloidy s uglom $\alpha$ :

$$\sin\alpha=\sqrt{1-\frac{y}{d}}.$ (4)$

S pomosh'yu etogo uravneniya mozhno provesti postroenie cikloidy. Zametim, chto v tochke A (x = 0, y = d), iz kotoroi ishodit cikloida, a = 0 i, sledovatel'no, kasatel'naya parallel'na osi OY. Smestivshis' na maluyu velichinu D vdol' osi OY, poluchim s pomosh'yu (4) novoe napravlenie kasatel'noi i, peremeshayas' vdol' etogo napravleniya opyat' na maluyu velichinu D, naidem novuyu tochku cikloidy, v kotoroi takim zhe sposobom smozhem opredelit' sleduyushee polozhenie kasatel'noi i t.d.

Itak, my priveli otvet, ne pokazav, kak on byl poluchen. Ne budem v tochnosti povtoryat' dokazatel'stvo Bernulli, no ispol'zuem ego osnovnuyu ideyu. On ishodil iz principa Ferma. Ved' minimum vremeni prohozhdeniya sveta, kak my videli v predydushem razdele, celikom opredelyaetsya vypolneniem zakona prelomleniya, svyazyvayushego sinusy uglov padeniya i otrazheniya so skorostyami sveta v sootvetstvuyushih sredah. Rassmotrim sloistuyu ploskuyu sredu, gde v kazhdom sloe svet imeet svoyu skorost'. Zakon prelomleniya v etom sluchae mozhet byt' vyrazhen sootnosheniem

$$\sin\alpha_i=ac_i,$ (5)$

gde $\alpha_i$ - ugol padeniya na granicu, razdelyayushuyu i-i i (i + 1)-i sloi, c_i - skorost' sveta v i-m sloe, a - nekotoraya konstanta, odinakovaya dlya vseh sloev.

Ochevidno, chto princip minimuma vremeni dvizheniya budet spravedliv i dlya material'noi tochki, esli dlya nee vypolnyaetsya analogichnoe sootnoshenie mezhdu velichinoi skorosti v dannoi tochke traektorii i sinusom ugla mezhdu napravleniem skorosti i napravleniem, perpendikulyarnym k ploskosti sloya, v kotorom absolyutnoe znachenie skorosti odinakovo. (Slova Bernulli: "Chto meshaet nam v etom sluchae postavit' odno na mesto drugogo?")

Skorost' tela pri ego dvizhenii v odnorodnom pole tyazhesti, kogda ono dvizhetsya bez treniya po nekotoroi poverhnosti (naprimer, po naklonnoi ploskosti), zavisit tol'ko ot vysoty padeniya: $v=\sqrt{2gh}$ , gde g - uskorenie svobodnogo padeniya, h - vysota padeniya. Takim obrazom, sloi, v kotoryh skorosti material'noi tochki odinakovy, raspolozheny gorizontal'no, a napravlenie, ortogonal'noe k ploskosti sloya, sovpadaet s napravleniem vertikali. Sledovatel'no, zadacha o brahistohrone svoditsya k nahozhdeniyu takoi krivoi, soedinyayushei dve zadannye tochki, dlya kotoroi sinus ugla mezhdu kasatel'noi k traektorii i vertikal'yu udovletvoryal by sootnosheniyu (5)

$$\sin\alpha=av=\sqrt{\frac{h}{b}},$ (6)$

gde b - poka proizvol'naya konstanta. Sravnivaya (6) s (4), my vidim, chto uravnenie sovpadaet s uravneniem cikloidy, prichem konstanta b imeet smysl diametra okruzhnosti, a h=d-y.

Nazad | Vpered

Publikacii s klyuchevymi slovami: geometricheskaya optika - fizika - variacionnyi princip Publikacii so slovami: geometricheskaya optika - fizika - variacionnyi princip
Sm. takzhe: Formula Einshteina Vsemirnyi god fiziki: triumf Einshteina Vneshnyaya ballistika pnevmaticheskogo oruzhiya Nobelevskaya premiya po fizike za 2004 god Pochemu u koshek devyat' zhiznei? Top-10 po fizike v 2003 godu URANIYa Nauchno-populyarnyi obrazovatel'nyi zhurnal v "Russkom pereplete" Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

Variacionnye principy v fizike

E. D. Trifonov

Vvedenie

Variacionnyi princip geometricheskoi optiki - princip Ferma

Zadacha o brahistohrone