Astronet > Variacionnye principy v fizike

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Variacionnye principy v fizike

E. D. Trifonov

Rossiiskii gosudarstvennyi pedagogicheskii universitet im. A.I. Gercena, Sankt-Peterburg

Teper' ostaetsya tol'ko podobrat' radius okruzhnosti dlya togo, chtoby cikloida proshla cherez vtoruyu zadannuyu tochku B. Vse cikloidy podobny drug drugu. Poetomu Bernulli predlozhil sleduyushee postroenie. Postroim kakuyu-nibud' cikloidu, ishodyashuyu iz pervoi tochki A. Postroim pryamuyu, prohodyashuyu cherez obe zadannye tochki A i B. Eta pryamaya peresechet postroennuyu cikloidu v nekotoroi tochke O (ris. 3, a). Radius okruzhnosti dlya iskomoi cikloidy otnositsya k radiusu postroennoi cikloidy kak otrezok AB k otrezku AO. Interesno, chto v nekotoryh sluchayah dlya bystreishego dostizheniya konechnoi tochki okazyvaetsya vygodnym predvaritel'no opustit'sya nizhe ordinaty etoi tochki (ris. 3, b).

Cikloida kak forma traektorii obladaet eshe odnim zamechatel'nym svoistvom, otkrytym Gyuigensom. Vremya dvizheniya tela po cikloide pod deistviem sobstvennoi tyazhesti do nizhnei ee tochki ne zavisit ot nachal'nogo polozheniya tela i prevyshaet vremya padeniya s vysoty h = d v p $\pi/2$ raz.

Zametim, chto reshenie dannoi zadachi I. Bernulli osnovano na kinematicheskoi optiko-mehanicheskoi analogii, otlichnoi ot dinamicheskoi analogii, kotoraya rassmatrivalas' nami v stat'e [2]. Ona nosit chisto kinematicheskii harakter. Dalee pereidem k vyvodu variacionnyh principov mehaniki, osnovannyh na dinamicheskoi optiko-mehanicheskoi analogii.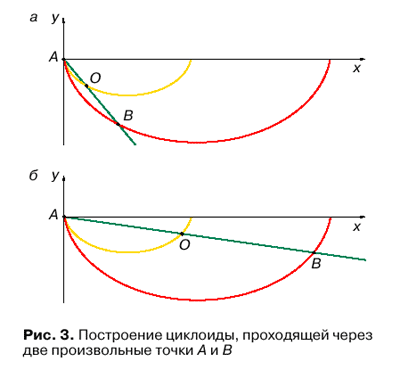

Princip naimen'shego deistviya Mopertyui

Napomnim, chto dinamicheskaya optiko-mehanicheskaya analogiya sostoit v tom, chto traektoriya material'noi tochki pri dvizhenii ee v potencial'nom pole U(x, y, z) i traektoriya lucha v opticheski neodnorodnoi srede s nepreryvno izmenyayushimsya pokazatelem prelomleniya n(x, y, z) v tochnosti sovpadayut, esli vypolnyaetsya sootnoshenie proporcional'nosti

$$n(x,y,z)~v(x,y,z)=\sqrt{\frac{2}{m}(E-U(x,y,z))},$ (7)$

gde m - massa material'noi tochki, u(x, y, z) - absolyutnaya velichina ee skorosti, E - energiya. Pri etom napravlenie skorosti v nachal'noi tochke sovpadaet s napravleniem lucha.

Vospol'zuemsya opyat' principom Ferma. Zapishem vremya rasprostraneniya sveta vdol' lucha. S etoi cel'yu razob'em luch, soedinyayushii dve fiksirovannye tochki, na N dostatochno malyh otrezkov $\Delta q_i$ , i=1,...,N. Pokazatel' prelomleniya sredy na kazhdom iz otrezkov oboznachim cherez n_i . Togda skorost' sveta na otrezke $\Delta q_i$ budet c/n_i , gde c - skorost' sveta v vakuume. Vremya rasprostraneniya sveta vdol' etogo otrezka ravno $\Delta q_in_i/c$ . Togda polnoe vremya rasprostraneniya sveta vdol' lucha mozhno predstavit' v vide summy

$$t=\frac{1}{c}\sum\limits^N_{i=1}n\Delta q_i.$ (8)$

Soglasno principu Ferma, eta summa, vychislennaya dlya istinnogo hoda lucha, dolzhna byt' minimal'noi po sravneniyu s takimi zhe summami dlya lyuboi dostatochno blizkoi vymyshlennoi ili, kak govoryat, virtual'noi formy lucha, prohodyashego cherez te zhe dve tochki.

Poskol'ku hod lucha sovpadaet s traektoriei dvizheniya material'noi tochki pri opredelennom sootvetstvii, vyrazhaemom formuloi (7), mezhdu potencial'nym polem i pokazatelem prelomleniya, to ochevidno, chto analogichnyi variacionnyi princip dolzhen vypolnyat'sya i v mehanike. Podstavlyaya v (8) vmesto pokazatelya prelomleniya n_i absolyutnoe znachenie skorosti material'noi tochki, umnozhennoe na massu, poluchim, chto velichina

$$W=\sum\limits^N_{i=1}mv_i\Delta q_i$ (9)$

dlya istinnoi traektorii, soedinyayushei dve zadannye tochki, prinimaet minimal'noe znachenie po sravneniyu so znacheniem etoi velichiny, vychislennoi dlya blizkoi virtual'noi traektorii, prohodyashei cherez te zhe dve tochki.

Velichinu W, stoyashuyu v levoi chasti (9), nazyvayut v mehanike deistviem, a sformulirovannyi vyshe variacionnyi princip, vyrazhaemyi etoi formuloi, - principom naimen'shego deistviya Mopertyui, poskol'ku v takoi forme on vpervye (1740) byl predlozhen francuzskim akademikom P'erom Mopertyui (1698-1759). Interesno, chto eto bylo sdelano pri ochen' smutnyh predstavleniyah ob optiko-mehanicheskoi analogii i yavilos' skoree schastlivoi dogadkoi, osnovannoi na teologo-filosofskih vozzreniyah avtora. Argumentiruya spravedlivost' vyskazannogo im principa, Mopertyui pochti tochno povtoryaet slova Ferma: "Priroda v svoih deistviyah vsegda pol'zuetsya naibolee prostymi sredstvami". Voznikli goryachie diskussii o spravedlivosti etogo principa (v kotoryh prinyal uchastie dazhe Vol'ter), a zatem ne menee goryachie spory o prioritete otkrytiya. Iz sovremennikov lish' Leonard Eiler (1707-1783) podderzhal Mopertyui, dokazav spravedlivost' ego principa na konkretnyh primerah.

Princip naimen'shego deistviya Gamil'tona

Sleduyushii vazhnyi shag v razvitii variacionnyh principov byl sdelan Uil'yamom Gamil'tonom (1805-1865) (s biografiei i tvorcheskoi zhizn'yu Gamil'tona mozhno poznakomit'sya po knige [7]).

Gamil'ton predlozhil novuyu formu variacionnogo principa mehaniki. My proillyustriruem variacionnyi princip Gamil'tona na primere material'noi tochki, dvizhusheisya v potencial'nom pole, ne zavisyashem ot vremeni. V etom sluchae vypolnyaetsya zakon sohraneniya energii, to est' summa kineticheskoi i potencial'noi energii ne izmenyaetsya so vremenem:

$$E=\frac{m(v^2_x+v^2_y+v^2_z)}{2}+U(x,y,z)=const,$ (10)$

hotya koordinaty i sostavlyayushie skorosti chasticy yavlyayutsya funkciyami vremeni: x = x(t), y = y(t), z = z(t), u_x = u_x(t), u_y = u_y(t), u_z = u_z(t). Pust' chastica dvizhetsya tak, chto v nachal'nyi moment vremeni t = 0 ona nahoditsya v tochke s koordinatami x₀ , y₀ , z₀ , a v moment vremeni t = T - v tochke s koordinatami x₁ , y₁ , z₁ .

Razob'em traektoriyu dvizheniya na intervaly $\Delta q_i$ , kotorye chastica prohodit za malye promezhutki vremeni Dti (poslednie mozhno schitat' ravnymi po velichine). Togda skorost' na i-m intervale budet $u_i = \Delta q_i/\Delta t_i$ .

Zapishem teper' deistvie dlya etogo dvizheniya, pribaviv k nemu konstantu -ET. Ispol'zuya ochevidnoe ravenstvo $\sum\limits_i\Delta t_i = T$ , poluchim

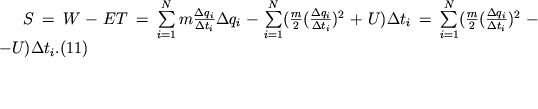
$S=W-ET=\sum\limits^N_{i=1}m\frac{\Delta q_i}{\Delta t_i}\Delta q_i - \sum\limits^N_{i=1}(\frac{m}{2}(\frac{\Delta q_i}{\Delta t_i})^2 + U)\Delta t_i = \sum\limits^N_{i=1}(\frac{m}{2}(\frac{\Delta q_i}{\Delta t_i})^2 - -U)\Delta t_i. (11)$

Vvedennuyu takim obrazom velichinu S takzhe nazyvayut deistviem, a chtoby ne bylo putanicy, velichinu W - ukorochennym deistviem. My vidim, chto dlya istinnogo dvizheniya deistvie S imeet minimal'noe znachenie po sravneniyu s ego znacheniyami na virtual'nyh traektoriyah, tochki kotoryh v nachal'nyi i konechnyi momenty vremeni sovpadayut sootvetstvenno s nachal'nym i konechnym polozheniyami material'noi tochki.

Hotya eto utverzhdenie sleduet iz principa naimen'shego deistviya Mopertyui, okazalos', chto ono imeet bol'shuyu oblast' primenimosti i vypolnyaetsya takzhe dlya sluchaya, kogda potencial'naya energiya zavisit ot vremeni. Prichem pri vybore virtual'nyh koordinat material'noi tochki mozhno ne zabotit'sya o sohranenii energii. V teh sluchayah, kogda potencial'naya energiya ne zavisit yavno ot vremeni, dlya istinnogo dvizheniya polnaya energiya budet sohranyat'sya avtomaticheski. Obratim vnimanie takzhe na to, chto v variacionnom principe Gamil'tona mozhno var'irovat' (to est' izmenyat' dlya sravneniya velichiny deistviya S) ne tol'ko formu traektorii (kak v principe Mopertyui), no i harakter dvizheniya po nei s techeniem vremeni. Pri etom dolzhno tol'ko vypolnyat'sya uslovie: polnoe vremya dvizheniya fiksirovano.

Itak, princip naimen'shego deistviya Gamil'tona mozhno sformulirovat' sleduyushim obrazom. Deistvie S dlya istinnogo dvizheniya material'noi tochki, traektoriya kotorogo v nachal'nyi i konechnyi momenty vremeni prohodit cherez dve opredelennye tochki, prinimaet minimal'noe znachenie po sravneniyu s lyubymi virtual'nymi dvizheniyami, traektorii kotoryh v ukazannye momenty vremeni prohodyat cherez te zhe dve tochki.

Iz-za nedostatka mesta my ne privodim zdes' konkretnyh primerov, podtverzhdayushih spravedlivost' principov Mopertyui i Gamil'tona. Ucheniku mozhno rekomendovat' samostoyatel'no ubedit'sya v etom na primere svobodnogo padeniya tela v odnorodnom pole tyazhesti. Eto mozhno sdelat' analiticheski, esli uchenik znakom s integrirovaniem elementarnyh funkcii, ili s pomosh'yu komp'yutera, kotoryi stanovitsya vse bolee dostupnym dlya shkol'nogo obucheniya.

Zaklyuchenie

Kratko ostanovimsya na roli, kotoruyu sygrali variacionnye principy v razvitii fiziki.

Posle formulirovki variacionnyh principov v forme Mopertyui i Gamil'tona byli predlozheny i drugie variacionnye principy mehaniki. Ih obshee znachenie zaklyuchalos' v tom, chto s ih pomosh'yu udavalos' edinym metodom poluchat' uravneniya dvizheniya slozhnyh mehanicheskih sistem. (V osnovnoi chasti stat'i my ne zatragivali etogo vazhnogo etapa primeneniya variacionnyh principov, poskol'ku eto trebuet dostatochno slozhnogo, i ne tol'ko dlya shkol'nikov, matematicheskogo apparata.) V dal'neishem bylo pokazano, chto variacionnye principy vozmozhny i v drugih razdelah fiziki, naprimer v elektrodinamike i special'noi teorii otnositel'nosti.

Variacionnye principy, voznikshie iz konkretnyh fizicheskih zadach, obogatili i samu matematiku. Odnoi iz obshih variacionnyh zadach, poyavivsheisya pochti odnovremenno s zadachei o brahistohrone, byla zadacha o geodezicheskoi linii: trebuetsya naiti liniyu naimen'shei dliny, soedinyayushuyu dve zadannye tochki na nekotoroi poverhnosti. Pozzhe eta zadacha byla obobshena na sluchai mnogomernyh prostranstv s neevklidovoi geometriei i vernulas' v fiziku v obshei teorii otnositel'nosti, gde rol' geodezicheskih v chetyrehmernom prostranstve-vremeni igrayut uravneniya dvizheniya material'noi tochki. V chastnosti, geodezicheskoi s nulevoi "dlinoi" yavlyaetsya uravnenie dvizheniya chasticy so skorost'yu sveta. Tak poyavilsya ochen' vazhnyi aspekt, svyazyvayushii fiziku i geometriyu prostranstva, kotoraya okazalas' zavisyashei ot real'nogo raspredeleniya mass.

Variacionnye principy i fizicheskaya ideya ob optiko-mehanicheskoi analogii imeli opredelyayushee znachenie dlya rozhdeniya volnovoi i kvantovoi mehaniki. V etom mozhno legko ubedit'sya, esli zaglyanut' v original'nye raboty Lui de Broilya i E. Shredingera (sm. perevody etih rabot v knige [3]). Variacionnye principy primenyayutsya i v kvantovoi teorii polya, yavlyayusheisya bazoi dlya issledovaniya elementarnyh chastic.

Vy vidite, chto rozhdennye usiliyami geniev variacionnye principy mehaniki i optiki okazali ogromnoe vliyanie na posleduyushee razvitie vsei fiziki, - vliyanie, prostirayusheesya do nashih dnei i daleko ne ischerpannoe.

Literatura

1. N'yuton I. Matematicheskie nachala natural'noi filosofii. M.: Nauka, 1989. 688 s.

2. Trifonov E.D. Optiko-mehanicheskaya analogiya v izlozhenii dlya shkol'nikov // Sorosovskii Obrazovatel'nyi Zhurnal. 1997. N 10. S. 133-137.

3. Variacionnye principy mehaniki: Sb. st. / Pod red. L.S. Polaka. M.: Gos. izd-vo fiz.-mat. lit., 1959. 932 s.

4. Gyuigens H. Traktat o svete. M.; L., 1935.

5. Kudryavcev P.S. Istoriya fiziki. M.: Uchpedgiz, 1948. T. 1. 535 s.

6. Sivuhin D.V. Obshii kurs fiziki: Optika. M.: Nauka, 1980. 751 s.

7. Polak L.S. Uil'yam Gamil'ton. M.: Nauka, 1993. 270 s.

Nazad | K soderzhaniyu

Publikacii s klyuchevymi slovami: geometricheskaya optika - fizika - variacionnyi princip Publikacii so slovami: geometricheskaya optika - fizika - variacionnyi princip
Sm. takzhe: Formula Einshteina Vsemirnyi god fiziki: triumf Einshteina Vneshnyaya ballistika pnevmaticheskogo oruzhiya Nobelevskaya premiya po fizike za 2004 god Pochemu u koshek devyat' zhiznei? Top-10 po fizike v 2003 godu URANIYa Nauchno-populyarnyi obrazovatel'nyi zhurnal v "Russkom pereplete" Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce