Na saite Astrometriya Astronomicheskie instrumenty Astronomicheskoe obrazovanie Astrofizika Istoriya astronomii Kosmonavtika, issledovanie kosmosa Lyubitel'skaya astronomiya Planety i Solnechnaya sistema Solnce

Kak na samom dele vyglyadit chernaya dyra?
7.05.2002 20:02 | M. E. Prohorov/GAISh, Moskva

Navernoe ya ne sovsem tochno sformuliroval svoi vopros - to o chem poidet rech' nel'zya uvidet' ne tol'ko glazom, no i v teleskop (dazhe v rentgenovskii ili radio). No voobrazhaemye veshi - nashe predstavlenie o predmete - ne menee real'no, chem to, chto my nablyudaem.

Rech' poidet o "forme" chernoi dyry, prichem chernoi dyry vrashayusheisya (ili Kerrovskoi - po imeni Kerra, togo kto pervym vyvel matematicheskoe opisanie takih dyr).

V 1963 godu matematik iz Novoi Zelandii Roi Kerr (Roy Kerr) poluchil tochnoe (analiticheskoe) reshenie dlya vrashayusheisya chernoi dyry. [Foto 1975 goda.]

Nevrashayushiesya chernye dyry tozhe imeyut slozhnuyu vnutrennyuyu strukturu (sm. opisanie resheniya Shvarcshil'da i resheniya dlya chernoi dyry s elektricheskim zaryadom (chernaya dyra Raisnera-Nordstrema)), no forma vseh ih poverhnostei mozhet byt' tol'ko sfericheskoi.

Ris. 1. Klassicheskoe izobrazhenie vrashayusheisya chernoi dyry (sm., naprimer, knigu U.Kaufmana).

Esli vy uzhe interesovalis' chernymi dyrami ili Obshei teoriei otnositel'nosti, to vam uzhe mogla vstrechat'sya kartinka, pokazannaya na ris.1. Na nei pokazany v razreze dve poverhnosti. Sfericheskaya - eto gorizont chernoi dyry. Ni odna material'naya chastica, dazhe fotony, ne mogut vyiti iz pod gorizonta, vse oni padayut k centru chernoi dyry. A splyusnutaya poverhnost' nazyvaetsya ergosferoi, chasticy vnutri nee mogut uderzhat'sya ot padeniya v chernuyu dyru, no obyazany vrashat'sya vmeste s nei (v tom zhe napravlenii, chto i chernaya dyra, no s razlichnymi skorostyami, zavisyashimi ot polozheniya chasticy v ergosfere). Eti dve poverhnosti kasayutsya drug druga na polyusah chernoi dyry, t.e. na osi ee vrasheniya, a na ekvatore razmery ergosfery bol'she, chem u gorizonta. Takim interesnym obrazom vo vrashayushihsya chernyh dyrah proyavlyayutsya "centrobezhnye sily". [Podrobnee o svoistvah vrashayushihsya chernyh dyr mozhno prochitat' v sootvetstvuyushei glave knigi Kaufmana.]

Obrashaem vashe vnimanie, chto pokazannye na ris.1 poverhnosti kasayutsya drug druga gladkim obrazom, chto v obshem-to ne udivitel'no, poskol'ku po forme ergosfera pohozha na splyusnutyi ellipsoid.

Tak vot - eto ne verno!

Samye neterpelivye mogut posmotret' na ris.3, a dlya ostal'nyh my ob'yasnim vse podrobnee.

Matematicheskie issledovaniya geometrii chernyh dyr pokazali, chto dvumernaya poverhnost' ergosfery vblizi polyusov obladaet konicheskimi osobennostyami. Chto eto oznachaet? Okruzhnost' radiusa r - eto krivaya, kazhdaya tochka kotoroi nahoditsya ot ee centra (tochki O) na rasstoyanii r. Esli okruzhnost' narisovana na ploskosti (chto my obychno i vidim), to otnoshenie ee dliny l k radiusu r budet ravno

No okruzhnosti mozhno risovat' i na krivyh poverhnostyah, togda otnoshenie ee dliny i radiusa (kotoryi otschityvaetsya vdol' poverhnosti) budet otlichat'sya ot . Odnako lyubaya gladkaya poverhnost', esli rassmatrivat' ee v nebol'shih masshtabah, stanovitsya vse bolee i bolee pohozhei na ploskost'. (Zdes' mozhno privesti mnogo primerov iz matematiki, geometrii i, dazhe, kosmologii, no ya ne budu etogo delat'.) Matematicheski eto vyrazhaetsya tak:

dlya gladkoi poverhnosti pri .

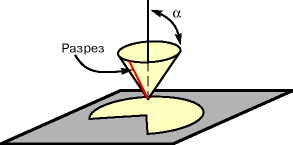Ris. 2. Illyustraciya umen'sheniya dliny okruzhnosti na konicheskoi poverhnosti.

Etot vyvod narushaetsya, esli poverhnost' ne yavlyaetsya gladkoi i vy risuete okruzhnost' imenno vokrug osoboi tochki. Samyi izvestnyi primer takoi poverhnosti - konus (a osobaya tochka, konechno, ego vershina). Na konuse s uglom polurastvora otnoshenie dliny okruzhnosti k radiusu ravno , t.e. ona vsegda men'she . Takoi vyvod legko mozhno sdelat' i po-drugomu, esli razrezat' konus po obrazuyushei (kak pokazano na ris.2), to on bez razryvov i rastyazheniya razvorachivaetsya na ploskost' v kotoroi budet ne hvatat' sektora (kak v piroge ih kotorogo uzhe otrezali kusok). Sootvetstvenno i dlina okruzhnosti okazhetsya men'she. Obrashayu vashe vnimanie, chto etot razrez sdelali my s vami dlya togo, chtoby razvernut' poverhnost' konusa na ploskost'. Ego mozhno bylo provesti i v lyubom drugom teste, tak kak na samom konuse nikakih osobennostei ne bylo.

Ris. 3. Klassicheskoe izobrazhenie vrashayusheisya chernoi dyry (sm., naprimer, knigu U.Kaufmana).

Imenno takie konicheskie osobennosti geometrii byli obnaruzheny vblizi polyusov ergosfery Kerrovskoi chernoi dyry. A dlya togo, chtoby ih "uvidet'", eti poverhnosti (ergosferu i gorizont) vlozhili v ploskoe Evklidovo prostranstvo. (Chto eto takoe? Kak eto bylo sdelano? Vsegda li takoe vlozhenie vozmozhno? Otvet na eti voprosy vy smozhete naiti v original'noi stat'e gr-qc/0012052. K sozhaleniyu ona na angliiskom.) Rezul'tat takogo vlozheniya pokazan na ris.3. Kak vidite, ergosfera po prezhnemu kasaetsya gorizonta na polyusah, no eto kasanie ne gladkoe, a skoree napominaet prikosnovenie konchika avtoruchki k bumage.

Dlya osobo interesuyushihsya skazhu, chto prezhnii ris.1 ne soderzhit nikakoi matematicheskoi oshibki, prosto on narisovan v "ochen' krivoi sisteme koordinat" (a obshaya teoriya otnositel'nosti imeet delo v osnovnom imenno s takimi iskrivlennymi prostranstvami), kotoraya "zamaskirovala" konicheskie osobennosti u polyusov.

Avtor prinosit ogromnuyu blagodarnost' Dipaku Baskaranu, obrativshemu moe vnimanie na rabotu Palevasa i dr. (gr-qc/0012052), i za mnogochislennye posleduyushie raz'yasneniya.

[Illyustraciya v zagolovke stat'i pokazyvaet geometriyu kerrovskoi chernoi dyry, vozmushennuyu padayushei na nee gravitacionnoi volnoi. Izobrazhenie vzyato s saita "International Art & Science" (http://www.i-a-s.de/). ]

Publikacii s klyuchevymi slovami: chernye dyry - reshenie Kerra - gorizont sobytii - ergosfera Publikacii so slovami: chernye dyry - reshenie Kerra - gorizont sobytii - ergosfera
Sm. takzhe: Porfirion: samyi dlinnyi dzhet ot chernoi dyry Tumannost' Tyul'pan i chernaya dyra Lebed' X-1 Chernaya dyra razrushaet zvezdu: animaciya Sliyanie dvuh chernyh dyr: modelirovanie Galaktika, dzhet i znamenitaya chernaya dyra Akkrecionnyi disk chernoi dyry: vizualizaciya Akkreciruyushaya chernaya dyra s dzhetom Vse publikacii na tu zhe temu >>