Astronet > Ya.B.Zel'dovich, "Vozmozhno li obrazovanie Vselennoi "iz nichego"?

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Vozmozhno li obrazovanie Vselennoi "iz nichego"?

<< Sohranenie energii | Oglavlenie | O spontannom rozhdenii >>

ASTROFIZIChESKIE VYVODY. NUZhNA LI PUL'SIRUYuShAYa VSELENNAYa?

Astrofizicheskie sledstviya zamknutosti Vselennoi podrobno rassmotreny v moei predydushei stat'e v "Prirode"^*).

Pervoe sledstvie sostoit v tom, chto obshaya plotnost' vseh vidov materii dolzhna byt' dostatochno velika; takim obrazom, poyavlyaetsya dopolnitel'nyi argument v pol'zu kakih-to form "skrytoi massy", poskol'ku plotnost' obychnyh horosho izvestnyh form massy (protonov, yader, elektronov, fotonov) nedostatochna.

Vtoroi vyvod zaklyuchaetsya v tom, chto nablyudaemoe v nastoyashee vremya rasshirenie Vselennoi dolzhno v budushem smenit'sya szhatiem - rano ili pozdno, pritom, veroyatno, skoree ochen' pozdno, dazhe po sravneniyu s segodnyashnim vozrastom Vselennoi^**).

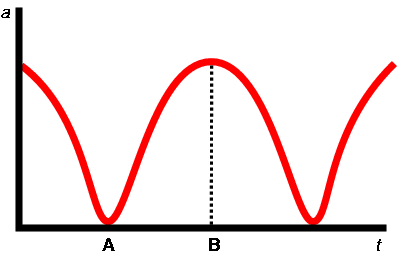Zavisimost' radiusa zamknutoi Vselennoi a ot vremeni v teorii ciklicheskoi evolyucii. V tochke A (radius minimalen) proishodit perehod ot szhatiya k rasshireniyu, v tochke B (radius maksimalen) rasshirenie smenyaetsya szhatiem.

Ideya zamknutogo mira, sperva rasshiryayushegosya, a potom szhimayushegosya, natalkivala mnogih uchenyh na gipotezu pul'siruyushei vechnoi Vselennoi. Delo ostavalos' za malym - v perenosnom i bukval'nom smysle slova: ponyatno, kak proishodit ostanovka i smena rasshireniya szhatiem pri bol'shom (maksimal'nom) radiuse Vselennoi, ostalos' ponyat', kak proishodit perehod ot szhatiya k rasshireniyu pri malom (minimal'nom) radiuse. Populyarnost' idei vechnoi (v proshlom!) Vselennoi vozrosla, kogda bylo osoznano, chto pri uchete polyarizacii vakuuma kriviznoi prostranstva (sil'nym gravitacionnym polem) ili za schet gravitacionnogo polya, istochnikom kotorogo yavlyaetsya skalyarnoe pole s neravnoi nulyu massoi, deistvitel'no sushestvuyut formal'no pravil'nye strogie resheniya ^***) tipa

$a(t) = \frac{1}{H_0} \ch\left(H_0 t\right) = \left.\left( e^{-H_0 t} + e^{+H_0 t}\right)\right/2H_0$

s minimal'nym radiusom 1/N₀ poryadka 10^-28 sm. Eti resheniya formal'no sushestvuyut i v klassicheskoi teorii. Kakie argumenty mozhno vydvinut' protiv etih reshenii?

Zavisimost' radiusa Vselennoi a ot vremeni t v teorii ciklicheskoi evolyucii pri uchete rosta entropii. Sovremennoe sostoyanie Vselennoi opisyvaetsya tochkoi V, t₀ - neobhodimoe "nachalo".

Lichno mne naibolee sushestvennym vozrazheniem predstavlyaetsya sama vozmozhnost' rozhdeniya Vselennoi "iz nichego". Ideya vechnoi Vselennoi kazalas' neizbezhnoi (mozhno bylo sporit' tol'ko o sposobe, v chastnosti klassicheskom ili kvantovom, perehoda ot szhatiya k rasshireniyu), do teh por poka kazalos', chto energiya i barionnyi zaryad - vechnye, sohranyayushiesya i pritom ne ravnye nulyu velichiny. Ot gipnoza etih idei my osvobodilis'. Esli gipoteza vechnoi Vselennoi ne obyazatel'na, to mozhno obratit'sya k detalyam, kasayushimsya teorii ciklicheskoi evolyucii.

Eshe v 30-e gody byl vydvinut ser'eznyi termodinamicheskii argument protiv vechnoi ciklicheski povtoryayusheisya Vselennoi. V hode kazhdogo cikla entropiya rastet ^****). Eto privodit k tomu, chto amplituda kazhdogo sleduyushego cikla bol'she amplitudy predydushego. Obrashaya etot argument v proshloe, mozhno sdelat' vyvod, chto konechno obshee chislo ciklov, nachinaya s pervogo cikla s nulevoi entropiei. No v takom sluchae cel' ne dostignuta - ciklicheski evolyucioniruyushaya Vselennaya vse ravno okazyvaetsya sushestvuyushei konechnoe vremya, t. e. nuzhdaetsya v "nachale".

V samoe poslednee vremya vmeste s V. A. Belinskim, L. P. Grishukom i I. M. Halatnikovym my analizirovali rasshirenie i szhatie Vselennoi, zapolnennoi massivnym kogerentnym skalyarnym polem ^*****).

Analogichnye raschety provodilis' i ranee, no, mozhet byt', s menee chetkimi vyvodami. Ne vdavayas' v podrobnosti, privozhu rezul'taty. V zavisimosti ot togo, yavlyaetsya li skalyarnoe pole $\varphi$ pochti statichnym $(m\varphi^2 \gg h{\varphi'}^2)$ ili bystromenyayushimsya i pochti bezmassovym $(m\varphi^2 \ll h{\varphi'}^2)$ , menyaetsya sootnoshenie mezhdu davleniem i plotnost'yu energii (zdes' h = 10^-14 Dzh^.s - postoyannaya Planka, shtrih - proizvodnaya $\varphi$ po vremeni). V pervom sluchae $p=-\varepsilon$ , imeet mesto gravitacionnoe ottalkivanie, vo vtorom sluchae, kogda davlenie maksimal'no veliko, $p=+\varepsilon$ - gravitacionnoe prityazhenie.

V principe, i pri szhatii, i pri rasshirenii mogut imet' mesto oba sluchaya. Odnako pri szhatii ustoichivym yavlyaetsya vtoroi rezhim, $p=+\varepsilon$ - davlenie polya soprotivlyaetsya szhatiyu. V takom sluchae klassicheskoe reshenie privodit v singulyarnost', radius Vselennoi obrashaetsya v nul', krivaya szhatiya utykaetsya v os' absciss. Resheniya s plavnym perehodom ot szhatiya k rasshireniyu okazyvayutsya isklyuchitel'nymi, maloveroyatnymi. No delo dazhe ne v detal'nom issledovanii krivyh. Bolee vazhen analiz teh predpolozhenii, kotorye prihoditsya delat' v hode resheniya zadachi.
Singulyarnoe szhatie Vselennoi pri polozhitel'nom davlenii $p=+\varepsilon$ . Zakon szhatiya odinakov dlya zamknutogo, ploskogo i otkrytogo mira: a ~ (t₀-t)^1/3 (sleduet imet' v vidu, chto t $\leq$ t₀).

My rassmatrivaem strogo odnorodnoe skalyarnoe pole i strogo odnorodnuyu i izotropnuyu Vselennuyu. Odnorodnost' oznachaet odinakovost', ekvivalentnost' vseh prostranstvennyh tochek v odin i tot zhe fiksirovannyi moment vremeni. Izotropiya oznachaet ekvivalentnost' vseh prostranstvennyh napravlenii.

V zadache o rasshirenii eti predpolozheniya razumny: v hode rasshireniya bystree vsego rasshiryaetsya oblast', v kotoroi skalyarnoe pole maksimal'no. Pri etom klassicheskoe skalyarnoe pole stanovitsya prakticheski postoyannym, a vse drugie polya (v chastnosti, narushayushee izotropiyu elektromagnitnoe pole) bystro ubyvayut.

Ne ostanavlivayas' na detalyah, avtor takogo scenariya A.D.Linde schitaet rasshirenie "estestvennym" i privodyashim k nablyudaemoi kartine Vselennoi ^******).

Odnako v hode szhatiya mozhno ozhidat' ogromnoi neustoichivosti, narusheniya odnorodnosti i izotropii. Poetomu variant prohozhdeniya Vselennoi nekoego minimal'nogo radiusa stanovitsya eshe menee veroyatnym pri uchete vozmushenii. Po sushestvu argument etot blizok k soobrazheniyam o vozrastanii entropii. Itak, esli eto i ne teorema, to vse zhe my imeem dostatochno pobuditel'nyh prichin dlya razmyshlenii o spontannom rozhdenii Vselennoi, ustranyayushem ideyu ciklicheskoi Vselennoi.

<< Sohranenie energii | Oglavlenie | O spontannom rozhdenii >>

Publikacii s klyuchevymi slovami: Kosmologiya - spontannoe rozhdenie Vselennoi - zakony sohraneniya - fizika elementarnyh chastic Publikacii so slovami: Kosmologiya - spontannoe rozhdenie Vselennoi - zakony sohraneniya - fizika elementarnyh chastic
Sm. takzhe: Podtverzhdennaya precessiya myuonov ostaetsya neob'yasnimoi Razlozhenie dalekogo sveta Formirovanie galaktik v magnitnoi Vselennoi "Effekty" Zel'dovicha, zapechatlennye na nashem nebe Sverhnovaya 1994D i neozhidannaya Vselennaya Kuda smeshaetsya krasnoe smeshenie? Samaya dalekaya sverhnovaya tipa Ia Vse publikacii na tu zhe temu >>

Mneniya chitatelei [11]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce