Astronet > Ya.B.Zel'dovich, "Vozmozhno li obrazovanie Vselennoi "iz nichego"?

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Vozmozhno li obrazovanie Vselennoi "iz nichego"?

<< Astrofizicheskie vyvody ... | Oglavlenie | Posleslovie >>

O SPONTANNOM ROZhDENII

Znamenityi do revolyucii yumorist A. Averchenko nachinal svoyu "Vsemirnuyu istoriyu" slovami: "Istoriya midyan temna i neponyatna. Uchenye delyat ee, tem ne menee, na tri perioda: pervyi, o kotorom rovno nichego ne izvestno. Vtoroi, kotoryi posledoval za pervym. I, nakonec, tretii period, o kotorom izvestno stol'ko zhe, skol'ko i o pervyh dvuh".

Boyus', chto poslednyaya chast' moei stat'i o rannei istorii Vselennoi budet pohozha na drevnyuyu istoriyu chelovechestva v izlozhenii A. Averchenko. Do sih por my vyyasnyali tol'ko principial'nuyu vozmozhnost' rozhdeniya Vselennoi. Chto mozhno skazat' o konkretnom mehanizme etogo yavleniya? Pridetsya ogranichit'sya postanovkoi voprosov.

Prezhde vsego, slovom "nichego", "iz nichego" mozhno pridavat' raznye traktovki. Mozhno predstavit' sebe pustoe ploskoe prostranstvo Minkovskogo - samo po sebe takoe reshenie uravnenii OTO sushestvuet i ono vechnoe. Rozhdenie mozhno bylo by predstavit' sebe napodobie serii kartinok (sm. ris).

Rozhdenie zamknutoi Vselennoi (sharik na poslednei chasti IV ris.) iz ploskogo mira Minkovskogo (M na stadii I). Na promezhutochnyh stadiyah, vdali ot fluktuacii, privodyashei k rozhdeniyu (otshepleniyu) sharika, metrika ostaetsya ploskoi ("minkovskoi").

Nado tol'ko pomnit', chto v nih rech' idet ob odnomernoi analogii. Izobrazhat' rozhdenie trehmernogo zamknutogo prostranstva (iz trehmernogo secheniya) prostranstva Minkovskogo ya ne umeyu. Vremya t&nbap; est' parametr, otlichayushii odnu chast' kartinki (I-IV) ot drugoi. Posle otdeleniya zamknutoi oblasti ostayusheesya prostranstvo snova ploskoe. No ved' ono ploskoe tol'ko v klassicheskom predele. V deistvitel'nosti v kvantovoi teorii metrika prostranstva tozhe fluktuiruet podobno tomu, kak oscillyator imeet opredelennuyu srednyuyu kineticheskuyu i takuyu zhe potencial'nuyu energiyu, ne ravnuyu nulyu v nizhnem energeticheskom sostoyanii.

Takim obrazom, na privedennom risunke rech' idet o fluktuacii - no o fluktuacii nastol'ko bol'shoi, chto menyaetsya sama topologiya, prostranstvo razdvaivaetsya. Rasschityvat' takie fluktuacii segodnya my ne umeem. Napomnyu, chto sami svoistva vakuuma (ego srednyuyu energiyu, t. e. kosmologicheskuyu postoyannuyu) my nahodim tol'ko iz opyta.

Vtoroi populyarnyi variant sostoit v rassmotrenii tol'ko odnogo zamknutogo mira (bez podstilayushego ili rozhdayushego ego prostranstva Minkovskogo). Togda do "nachala" ne bylo bukval'no nichego, nikakoi metriki, v chastnosti ne bylo i vremeni.

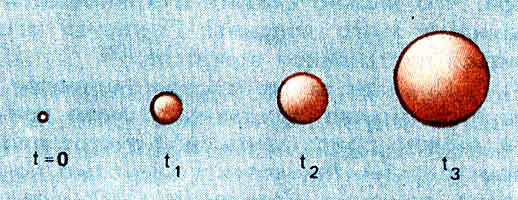Spontannoe rozhdenie mira "iz nichego". Do momenta t = 0 metrika (i, v chastnosti, vremya) ne sushestvovala.

Klassicheskie uravneniya dvizheniya ne imeyut resheniya nuzhnogo tipa. Znachit, sleduet iskat' kvantovomehanicheskie resheniya. Zadacha podobna zadache ob $\alpha$ -raspade yadra urana ili radiya. Po klassicheskoi n'yutonovskoi mehanike $\alpha$ -chastica ne mozhet proiti ves' put' ot yadra do beskonechnosti. Kvantovomehanicheskoe reshenie dlya $\alpha$ -chasticy opisyvaet obe oblasti: "podbar'ernuyu", v kotoroi kineticheskaya energiya otricatel'na (t. e. klassicheskoe dvizhenie nevozmozhno), i dalekuyu oblast', v kotoroi sushestvuyut oba resheniya - i klassicheskoe, i kvantovomehanicheskoe, i oni malo otlichayutsya drug ot druga.

Podobno teorii $\alpha$ -raspada stroitsya i kvantovomehanicheskaya teoriya rozhdeniya Vselennoi. Estestvenno, zadachu seichas reshayut lish' v samom grubom priblizhenii, rassmatrivaya vsego dve velichiny - radius zamknutoi Vselennoi a(t) i skalyarnoe pole $\varphi$ . V kvantovoi teorii vvodyatsya sootvetstvuyushie impul'sy R_a i R, stroitsya volnovaya funkciya $\Psi(a,\varphi).$ Impul's R_a = M_eff = f(a)a' - proporcionalen skorosti rasshireniya, i v klassicheskom predele mozhno naiti a' = da/dt, a znachit, i vremya

$t = \int \left(\frac{da}{dt}\right)^{-1} da\,.$

Zametim takzhe, chto kvantovaya teoriya dazhe v segodnyashnem nerazvitom ee sostoyanii daet argument v pol'zu zamknutoi Vselennoi (v otlichie ot beskonechnoi ploskoi ili otkrytoi Vselennoi). Tol'ko dlya zamknutoi Vselennoi mozhno opredelit' nekoe nebeskonechnoe znachenie effektivnoi massy M_eff. Kakoi by formulirovkoi kvantovoi mehaniki my ni pol'zovalis' (volnovaya funkciya, ili "integrirovanie po putyam", ili lyuboi inoi), veroyatnost' spontannogo rozhdeniya beskonechnoi Vselennoi tozhdestvenno ravna nulyu ^*).

V celom, odnako, interpretaciya poluchennyh rezul'tatov ostaetsya ne vpolne yasnoi. Kvantovomehanicheskie formuly ukazyvayut na vozmozhnost' rozhdeniya Vselennoi. Predstavlyayut interes rezul'taty v chasti sravneniya veroyatnosti rozhdeniya Vselennoi s tem ili inym nachal'nym znacheniem skalyarnogo polya p. Po-vidimomu, bolee veroyatny bol'shie znacheniya p, obespechivayushie dostatochno bol'shuyu inflyaciyu na klassicheskoi faze. Odnako net interpretacii absolyutnogo znacheniya volnovoi funkcii i veroyatnosti. Est' i bolee glubokie osnovaniya dlya skepsisa po otnosheniyu k konkretnym teoriyam rozhdeniya Vselennoi "iz nichego".

Delo v tom, chto razvitie fundamental'noi fiziki eshe yavno ne zakoncheno! Bolee togo, imenno seichas ozhivayut vse bolee geometrizovannye teorii elementarnyh chastic. S odnoi storony, eto. teorii, ob'edinyayushie bozony i fermiony, ob'edinyayushie vnutrennie peremennye chastic i polei s koordinatami i preobrazovaniyami Lorenca. V perspektive eti teorii dolzhny dat' i pryamoe dokazatel'stvo sushestvovaniya skalyarnyh polei, a takzhe opredelit' ih svoistva. Rano ili pozdno vozniknet i teoriya mass chastic, i fiziki skazhut nam, chto takoe skrytaya massa, kotoruyu otkryli astronomy. Eshe bolee blizkoe otnoshenie k voprosu o rozhdenii Vselennoi imeyut gipotezy o prostranstve-vremeni vysokoi razmernosti. Eshe v konce 20-h godov byla sformulirovana ideya, soglasno kotoroi est' odna "lishnyaya" koordinata H₄, svernutaya v kol'co dlinoi l=2 $\pi$ R, gde R - radius kol'ca^**). Shematicheski situaciya izobrazhena na risunke. Tri prostranstvennyh koordinaty X₁, H₂, H₃ - zameneny odnoi H vdol' trubki.

V kvantovoi teorii dvizhenie vdol' H₄ ili lokalizaciya chasticy pr koordinate H₄ trebuyut gigantskih energii. Poetomu vo vseh opytah vplot' do samyh bol'shih energii, 10¹⁷ ili dazhe 10¹⁹ GeV (sravnite s 10³ GeV na uskoritelyah 80-h godov), net dvizheniya po osoboi koordinate H₄ (ili ot H₄ do H₉). Teoretiki govoryat, chto v nizkoenergeticheskom predele prostranstvo-vremya ostaetsya effektivno chetyrehmernym. Esli k tomu zhe ogranichivat'sya razmerami, malymi po sravneniyu s astronomicheskimi, to prostranstvo i vremya opisyvayutsya staroi dobroi metrikoi Minkovskogo.

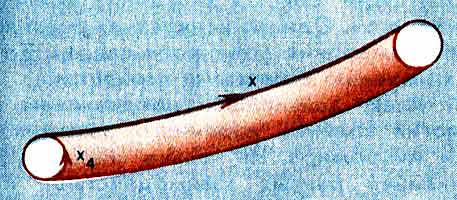Shematichnoe izobrazhenie prostranstva Kapucy-Kleina. Pokazano sechenie odnogo zadannogo znacheniya vremeni X₀= const, tri prostranstvennye koordinaty X₁, H₂, H₃ zameneny odnoi - X. V itoge poluchilas' dvumernaya poverhnost' trubki s koordinatami X, X₄ na poverhnosti.

I tem ne menee, vvedenie v rassmotrenie dopolnitel'nyh izmerenii - H₄ v prosteishem primere - ne prohodit bessledno. Mozhno rassmotret' malye izmeneniya metriki, pri kotoryh koordinatnaya os' dopolnitel'nogo izmereniya H₄ predpolagaetsya ne perpendikulyarnoi koordinatnoi setke osnovnyh (makroskopicheskih) izmerenii. Okazyvaetsya, chto effektivno takoe predpolozhenie ekvivalentno poyavleniyu elektromagnitnogo polya v obychnom prostranstve.

Uvelichenie chisla kompaktificirovannyh ("svernutyh") peremennyh s 1 do 6 ili 7 (perehod k 10-mernomu ishodnomu prostranstvu-vremeni) daet vozmozhnost' vvesti ne tol'ko elektromagnitnoe pole, no i te polya (W^�, Z�), kotorye opisyvayut slaboe vzaimodeistvie, i polya (glyuonnye), kotorye opisyvayut sil'noe vzaimodeistvie. K tomu zhe, teoriya supersimmetrii, ob'edinyayushaya bozonnye polya (takie, v chastnosti, kak elektromagnitnoe) i fermionnye polya (takie, kak elektron-pozitronnoe), tozhe "geometrichna", ona vvodit novye - udivitel'nye, no geometricheskie peremennye. Mechta A. Einshteina o geometrizacii vsei fiziki segodnya predstavlyaetsya gorazdo bolee real'noi, chem eto kazalos' vsego 5 ili 10 let nazad.

No pochemu ya pishu obo vsem etom v kosmologicheskoi stat'e?

Pervaya (ne samaya glavnaya) prichina sostoit v tom, chto my, nakonec, prisutstvuem pri rozhdenii teorii, dlya kotoryh skalyarnye polya yavlyayutsya neobhodimym sledstviem. O znachenii skalyarnyh polei uzhe govorilos' - bez nih ne bylo by inflyacionnoi Vselennoi. Polyarizaciya vakuuma kak istochnik energii i otricatel'nogo davleniya dlya inflyacii (razduvaniya) Vselennoi, est' tozhe raznovidnost' skalyarnogo polya.

Odnako bolee sushestven i bolee specifichen vtoroi aspekt vliyaniya teorii s "lishnimi" izmereniyami na kosmologiyu. V moment rozhdeniya v zamknutom mire prostranstvennye peremennye X₁, H₂, H₃ menyayutsya v ochen' uzkih predelah poryadka 0 < 2 $\alpha$ a(t), gde a(t) stremtsya k 0 pri t, stremyashemsya k 0. Estestvenno predpolozhit' v takom sluchae, chto v deistvitel'nosti Vselennaya rozhdaetsya simmetrichnoi po vsem prostranstvennym peremennym (razmernost' D = 5 ili vyshe). Razdelenie geometricheskih peremennyh na "vnutrennie", t. e. kompaktificirovannye, D = 4 peremennye i na obychnye geometricheskie tri peremennye i vremya proishodit lish' pozzhe. Eto razdelenie predstavlyaet soboi tipichnoe spontannoe (samoproizvol'noe) narushenie simmetrii! Pervonachal'no my imeem, naprimer, 9-mernyi "shar", vse napravleniya v kotorom ekvivalentny, a pozzhe 6 izmerenii zastyvayut s a₄-a₉ (ih harakternye razmery poryadka 10^-33 sm) ^***), a tri izmereniya rastut eksponencial'no i, v konce koncov, stanovyatsya bol'she 5000 Mpk = 10²⁸ sm, t. e. bol'she vsei nablyudaemoi oblasti Vselennoi. Namereniya u nas ostalis' te zhe, chto i ran'she,- opisat'rozhdenie Vselennoi "iz nichego". Odnako konkretnaya realizaciya etogo namereniya stanovitsya sovsem drugoi po sravneniyu s pervymi variantami.

Rozhdenie simmetrichnogo mira s koordinatami X₄ i X₁, H₂, H₃ pri "zamorazhivanii" X₄ (v moment t₂). Etot risunok sozdaet u chitatelya nepravil'noe vpechatlenie o neodnorodnosti prostranstva (bol'shaya krivizna na koncah ellipsa). Odnako nuzhno pomnit', chto v mnogomernoi geometrii sushestvuyut prostranstva (tak nazyvaemye resheniya Blanki), odnorodnye, no s raznoi kriviznoi po raznym napravleniyam. K sozhaleniyu, ya ne umeyu izobrazhat' ih na ploskosti risunka.

Itak, dal'neishee prodvizhenie kosmologii trebuet korennogo razvitiya fiziki mikromira. Ne tol'ko "Velikoe ob'edinenie" raznyh vzaimodeistvii, no i predstoyashee "Samoe velikoe ob'edinenie" mikromira i kosmologii - takova naibolee fundamental'naya i ambicioznaya programma konca XX veka.

<< Astrofizicheskie vyvody ... | Oglavlenie | Posleslovie >>

Publikacii s klyuchevymi slovami: Kosmologiya - spontannoe rozhdenie Vselennoi - zakony sohraneniya - fizika elementarnyh chastic Publikacii so slovami: Kosmologiya - spontannoe rozhdenie Vselennoi - zakony sohraneniya - fizika elementarnyh chastic
Sm. takzhe: Podtverzhdennaya precessiya myuonov ostaetsya neob'yasnimoi Razlozhenie dalekogo sveta Formirovanie galaktik v magnitnoi Vselennoi "Effekty" Zel'dovicha, zapechatlennye na nashem nebe Sverhnovaya 1994D i neozhidannaya Vselennaya Kuda smeshaetsya krasnoe smeshenie? Samaya dalekaya sverhnovaya tipa Ia Vse publikacii na tu zhe temu >>

Mneniya chitatelei [11]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce