Zhestkoe sinhrotronnoe izluchenie pri akkrecii veshestva na odinochnye chernye dyry zvezdnyh mass
<< 2. Fizika processov v ... | Oglavlenie | 2.2. Magnitnoe pole >>
2.1 Temp akkrecii, struktura techeniya i unifikaciya granichnyh uslovii
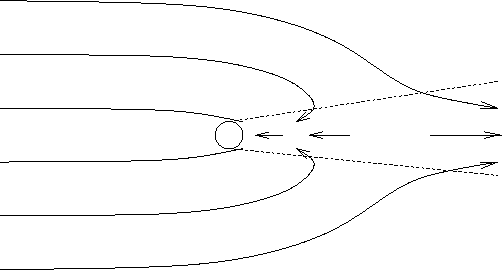 |
Ris. 1. Krupnomasshtabnaya struktura techeniya gaza vokrug chernoi dyry v sluchae ego sverhzvukovogo dvizheniya. Pokazana zona tormozheniya pozadi gravitiruyushego centra ("hvost" chernoi dyry, udarnaya volna), a takzhe zona sferizacii vblizi nego. |
Rassmotrim strukturu techeniya vokrug dvizhusheisya v mezhzvezdnoi srede chernoi dyry (ochevidno, na bol'shih masshtabah ona dolzhna obladat' cilindricheskoi simmetriei).
Voobshe govorya, zadacha sil'no uslozhnyaetsya iz-za besstolknovitel'nosti sredy[12] - dlina svobodnogo
probega chastic otnositel'no kulonovskih stolknovenii
zachastuyu znachitel'no prevoshodit harakternyi
masshtab zadachi - radius Bondi[25]
Odnako zadacha vse-taki ne svoditsya k sluchayu akkrecii nevzaimodeistvuyushih chastic (kotoraya byla rassmotrena, naprimer, v rabotah [18,28]) - situaciyu v kakoi-to mere spasaet nalichie magnitnogo polya[12] (rol' dliny svobodnogo probega nachinaet igrat' gorazdo men'shii larmorovskii radius), kotoroe pozvolyaet chasticam obmenivat'sya impul'som. Blagodarya etomu sreda v nekotorom smysle mozhet rassmatrivat'sya kak gidrodinamicheskaya (podobnaya situaciya izvestna v fizike plazmy - smotri [4]). Srazu zhe otmetim, chto nalichie vmorozhennogo magnitnogo polya pozvolyaet chasticam effektivno obmenivat'sya momentom, no ne energiei.
Temp akkrecii na dvizhushiisya gravitiruyushii centr fakticheski opredelyaetsya proishodyashim
vblizi osi dvizheniya pozadi chernoi dyry, gde veshestvo teryaet perpendikulyarnuyu
komponentu impul'sa - ee gasit vmorozhennoe v veshestvo magnitnoe pole (ili
razvitie puchkovyh neustoichivostei posle peresecheniya potokami chastic osi simmetrii pozadi gravitiruyushego
centra[6,43], gde skorost' perestaet byt' odnoznachnoi funkciei koordinat).
Razmer etoi zony (diametr "hvosta" chernoi dyry) opredelyaetsya rasstoyaniem ot osi,
na kotorom energiya magnitnogo polya stanovitsya sravnimoi s kineticheskoi energiei potoka, t.e.
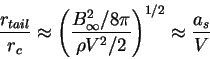
gde
Pri dal'neishem padenii na centr potok stanovitsya sfericheski-simmetrichnym[12] - eto vidno hotya by iz nesopostavimosti skorostei gaza na beskonechnosti so skorost'yu svobodnogo padeniya vblizi nee (eto podtverzhdaetsya kak prostymi teoreticheskimi argumentami[6,43], tak i chislennym modelirovaniem[41]).
Pri podobnoi strukture techeniya (primernyi vid ee pokazan na ris.1) temp akkrecii
ne zavisit ot togo, chto imenno ostanavlivaet veshestvo - gazovoe davlenie ili magnitnoe pole,
a potomu on opredelyaetsya toi zhe formuloi, chto
i v gidrodinamicheskoi zadache akkrecii na dvizhushiisya gravitiruyushii centr - formuloi
Hoila-Littltona[39]
gde
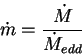
gde eddingtonovskii temp akkrecii
Dlya dal'neishih ocenok otnormiruem eto vyrazhenie na massu chernoi dyry
Otmetim eshe odno vazhnoe (i daleko ne ochevidnoe pri formal'nom rassmotrenii zadachi) sledstvie takoi struktury akkrecionnogo potoka. A imenno, v zone tormozheniya pozadi chernoi dyry proishodit pereraspredelenie energii akkrecionnogo potoka - veshestvo teryaet komponentu skorosti, perpendikulyarnuyu osi simmetrii, po poryadku velichiny ravnuyu skorosti na beskonechnosti, i eta dolya kineticheskoi energii perehodit v magnitnuyu (t.k. veshestvo ostanavlivaetsya magnitnym polem), prichem odnovremenno veshestvo dolzhno nagrevat'sya. Razumno predpolozhit', chto vse tri vida energii akkrecionnogo potoka v etoi zone uravnivayutsya, prichem vse oni stanovyatsya poryadka gravitacionnoi energii (uslovie zahvata) - ustanavlivaetsya ravnoraspredelenie energii, kotoroe, ochevidno, budet sohranyat'sya i v processe dal'neishego padeniya (eto znachit, chto otsutstvuyut myslimye pri formal'nom rassmotrenii effekty "magnitnoi i teplovoi otkachki"). Esli zhe sreda ne yavlyaetsya besstolknovitel'noi, to veshestvo v "hvoste" ostanavlivaetsya gazovym davleniem, i magnitnaya energiya v hvoste ne prihodit v ravnoraspredelenie (hotya i uvelichivaetsya po sravneniyu s polem na beskonechnosti) - v takom sluchae ravnoraspredelenie magnitnoi i gravitacionnoi energii ustanavlivaetsya v processe dal'neishego padeniya (a eto proishodit ochen' bystro pri lyubyh razumnyh parametrah)
Takim obrazom, my mozhem govorit' ob unifikacii granichnyh uslovii zadachi i schitat', chto na nekotorom dostatochnogo bol'shom radiuse potok sfericheski-simmetrichen i vse vidy energii odnogo poryadka - zadacha fakticheski svoditsya k sluchayu sfericheski-simmetrichnoi akkrecii na pokoyashuyusya chernuyu dyru, gde podobnoe ravnoraspredelenie ustanavlivaetsya prakticheski na radiuse zahvata. V dal'neishem imenno etu zadachu my i budem rassmatrivat'.
<< 2. Fizika processov v ... | Oglavlenie | 2.2. Magnitnoe pole >>
|
Publikacii s klyuchevymi slovami:
konkurs - chernye dyry - akkreciya - Sinhrotronnoe izluchenie - magnitnoe pole
Publikacii so slovami: konkurs - chernye dyry - akkreciya - Sinhrotronnoe izluchenie - magnitnoe pole | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |