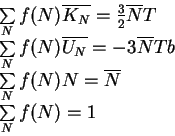Entropiya bol'shogo kanonicheskogo ansamblya v rasshiryayusheisya Vselennoi
<< 1. Vstuplenie | Oglavlenie | 3. Model'nyi konfiguracionnyi integral >>
2. Entropiya
Pust'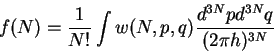 |
(1) |
Nasha zadacha seichas sostoit v tom, chtoby poluchit' vyrazhenie dlya
entropii cherez velichiny ![]() . Opredelenie entropii sleduyushee:
. Opredelenie entropii sleduyushee:
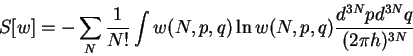 |
(2) |
gde
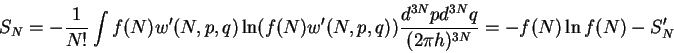
a velichiny
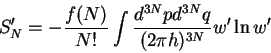 |
(3) |
Zdes' delaetsya vtoroe predpolozhenie. Relaksaciya po energii uzhe proizoshla, a po chislu chastic - net. Eto razumno, tak kak pervoe proishodit na rasstoyanii, v to vremya kak vtoroe svyazano s fizicheskim peremesheniem galaktik. Harakternoe vremya relaksacii po chislu chastic poetomu poryadka razmera rassmatrivaemogo ob'ema, delennogo na srednyuyu "teplovuyu" skorost' chastic. Dlya relaksacii zhe po energii harakternoe vremya est' skorost' chasticy, delennaya na vyzyvaemoe drugimi galaktikami uskorenie. Dlya skopleniya galaktik, soderzhashego v ob'eme 5 Mpk neskol'ko soten galaktik, s "teplovymi" skorostyami okolo dvuh-treh soten kilometrov v sekundu oni okazyvaeyutsya poryadka sootvetstvenno 10 i 1 milliardov let, tak chto relaksaciya po energii proishodit znachitel'no ran'she.
Relaksaciya i maksimizaciya entropii dlya nas - odno i to zhe. Poetomu
nado maksimizirovat' velichiny ![]() . Teper' vremya vspomnit' o
nalagaemyh na ansambl' usloviyah. Obychno, uchityvaya uravnenie Liuvillya, ishut
zavisimost' ot integralov dvizheniya, i dobavlyaya soobrazheniya o neobhodimosti
additivnosti poslednih, poluchayut raspredeniya Gibbsa. Odnako poslednie ne
kazhutsya ochevidnymi dlya gravitacionno svyazannyh sistem. Ni otkuda ne sleduet,
chto fiksiruetsya summarnaya energiya. Poetomu estestvennym kazhetsya vklyuchenie
ogranichenii po otdel'nosti na chislo chastic, kineticheskuyu i potencial'nuyu
energiyu, prichem pod poslednei imeetsya v vidu imenno energiya korrelyacii - to
est' raznica mezhdu realizuemoi pri dannoi konfiguracii
. Teper' vremya vspomnit' o
nalagaemyh na ansambl' usloviyah. Obychno, uchityvaya uravnenie Liuvillya, ishut
zavisimost' ot integralov dvizheniya, i dobavlyaya soobrazheniya o neobhodimosti
additivnosti poslednih, poluchayut raspredeniya Gibbsa. Odnako poslednie ne
kazhutsya ochevidnymi dlya gravitacionno svyazannyh sistem. Ni otkuda ne sleduet,
chto fiksiruetsya summarnaya energiya. Poetomu estestvennym kazhetsya vklyuchenie
ogranichenii po otdel'nosti na chislo chastic, kineticheskuyu i potencial'nuyu
energiyu, prichem pod poslednei imeetsya v vidu imenno energiya korrelyacii - to
est' raznica mezhdu realizuemoi pri dannoi konfiguracii ![]() i srednei v
dannom ob'eme. Zapishem eti usloviya, kotorye, sobstvenno i vydelyayut sistemy i
usloviya polnoi normirovki:
i srednei v
dannom ob'eme. Zapishem eti usloviya, kotorye, sobstvenno i vydelyayut sistemy i
usloviya polnoi normirovki:
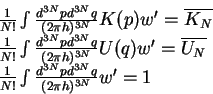 |
(4) |
Maksimiziruya
| (6) |
Dalee iz
![]() legko poluchit':
legko poluchit':
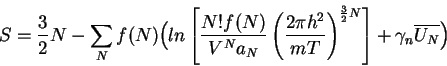 |
(7) |
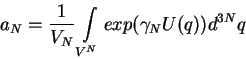
Dlya ![]() imeem uravnenie:
imeem uravnenie:
| (8) |
Itak, my poluchili vyrazhenie dlya entropii kak funkcii ![]() i
i
![]() .
.
<< 1. Vstuplenie | Oglavlenie | 3. Model'nyi konfiguracionnyi integral >>
|
Publikacii s klyuchevymi slovami:
Kosmologiya - galaktiki - Rasshirenie Vselennoi - gravitacionnoe skuchivanie galaktik - termodinamika - entropiya
Publikacii so slovami: Kosmologiya - galaktiki - Rasshirenie Vselennoi - gravitacionnoe skuchivanie galaktik - termodinamika - entropiya | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |