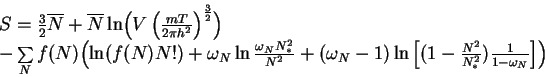Entropiya bol'shogo kanonicheskogo ansamblya v rasshiryayusheisya Vselennoi
<< 2. Entropiya | Oglavlenie | 4. Zaklyuchenie >>
3. Model'nyi konfiguracionnyi integral
Dlya vychisleniya konfiguracionnogo integrala vospol'zuemya standartnym Van der Vaal'sovskim sposobom. Hotya primenimost' ego zdes' vryad li obosnovanna v vidu dal'nodeistviya zatronutyh sil, v opravdanie mozhno privesti lish' otsutstvie drugih sposobov.
Itak, zamechaya, chto ![]() , ibo povedenie kineticheskoi i
potencial'noi energii, po-vidimomu, dolzhno byt' soglasovanno (sm. dalee),
i schitaya, chto potencial imeet formu yamy glubinoi
, ibo povedenie kineticheskoi i
potencial'noi energii, po-vidimomu, dolzhno byt' soglasovanno (sm. dalee),
i schitaya, chto potencial imeet formu yamy glubinoi ![]() i razmerom
i razmerom ![]() (
(
![]() ,
, ![]() - poryadka razmerov galaktiki), a takzhe
vychitaya iz nego srednyuyu energiyu, ravnuyu
- poryadka razmerov galaktiki), a takzhe
vychitaya iz nego srednyuyu energiyu, ravnuyu
![]() (
(![]() - koefficient
poryadka edenicy, zavisyashii ot formy ob'ema i ravnyi dlya shara
- koefficient
poryadka edenicy, zavisyashii ot formy ob'ema i ravnyi dlya shara
![]() ), imeem sleduyushie vyrazheniya:
), imeem sleduyushie vyrazheniya:
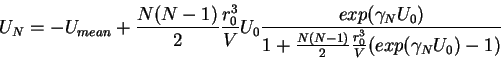
otkuda
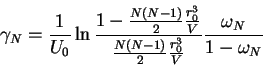 |
(9) |
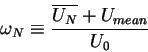 |
(10) |
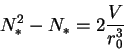 |
(11) |
Teper', posle nekotoryh perobrazovanii, mozhno poluchit' dlya entropii:
Uzhe otsyuda vidno, chto kvadratichnaya zavisimost' ![]() ot
ot ![]() ostavlyaet lish' prisushuyu ideal'nomu gazu chast' etogo vyrazheniya, no eto
govorit skoree o slabosti modeli, chem o nevozmozhnosti takogo povedeniya.
ostavlyaet lish' prisushuyu ideal'nomu gazu chast' etogo vyrazheniya, no eto
govorit skoree o slabosti modeli, chem o nevozmozhnosti takogo povedeniya.
Tem ne menee, my predpolozhim, chto povedenie ![]() takzhe lineino s
rostom chisla chastic. V kachestve obosnovaniya mozhno soslat'sya na raboty
(Layzer, 1963; Irvine, 1965), pokazavshih, chto v srednem vo Vselennoi
korrelyacionnaya chast' energii i kineticheskaya energiya vedut sebya soglasovanno
(stremyas' v itoge k virializovannomu sostoyaniyu). Sovmestno s usloviyami na
takzhe lineino s
rostom chisla chastic. V kachestve obosnovaniya mozhno soslat'sya na raboty
(Layzer, 1963; Irvine, 1965), pokazavshih, chto v srednem vo Vselennoi
korrelyacionnaya chast' energii i kineticheskaya energiya vedut sebya soglasovanno
(stremyas' v itoge k virializovannomu sostoyaniyu). Sovmestno s usloviyami na
![]() ,
, ![]() i vyrazheniem dlya
i vyrazheniem dlya ![]() , eto daet:
, eto daet:
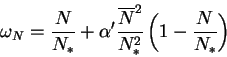
gde
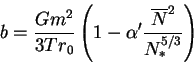
Eto vyrazhenie, s uchetom vseh nalozhennyh uslovii, uzhe mozhet imet'
otnoshenie k real'nosti i daet otlichnye ot nulya slagaemye, otvechayushie za
izmenenie entropii vzaimodeistviem. Ego uzhe mozhno ispold'zovat' - po krainei
mere, dlya dostatochno razrezhennyh sistem (a dlya tipichnyh skoplenii vypolneno,
chto
![]() ) - dlya otdaniya predpochteniya tomu ili drugomu
variantu raspredeleniya
) - dlya otdaniya predpochteniya tomu ili drugomu
variantu raspredeleniya ![]() .
.
Dlya vyrazheniya (12) s uchetom uslovii (5) mozhno reshit'
i bolee obshuyu zadachu s lyubymi razumnyni ![]() - naiti ekstremal'noe
raspredelenie
- naiti ekstremal'noe
raspredelenie ![]() , dostavlyayushee maksimum entropii. Priravnyav variacionnuyu
proizvodnuyu nulyu, poluchim:
, dostavlyayushee maksimum entropii. Priravnyav variacionnuyu
proizvodnuyu nulyu, poluchim:
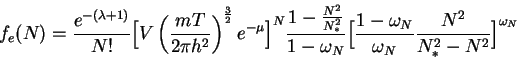 |
(13) |
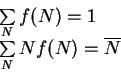
Eti formuly, tem ne menee, buduchi primeneny k konkretnym situaciyam, nesmotrya na kazhusheesya znachitel'noe otlichie, dayut raspredeleniya, blizkie k Puassonovomu. Dal'neishaya rabota neobhodima dlya bolee tshatel'nogo issledovaniya etogo voprosa.
<< 2. Entropiya | Oglavlenie | 4. Zaklyuchenie >>
|
Publikacii s klyuchevymi slovami:
Kosmologiya - galaktiki - Rasshirenie Vselennoi - gravitacionnoe skuchivanie galaktik - termodinamika - entropiya
Publikacii so slovami: Kosmologiya - galaktiki - Rasshirenie Vselennoi - gravitacionnoe skuchivanie galaktik - termodinamika - entropiya | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |