| << Predydushaya |
Metodika provedeniya 1
uroka
"Zakony dvizheniya kosmicheskih tel"
Cel' uroka: formirovanie ponyatiya o kosmicheskom yavlenii - dvizhenii kosmicheskih tel.
Zadachi obucheniya:
Obsheobrazovatel'nye: formirovanie ponyatii:
- o nebesnoi mehanike (o predmete,
metodah i instrumentah nebesnoi mehaniki,
ee svyazi s drugimi naukami i osnovnyh
etapah razvitiya);
- o kosmicheskom yavlenii – dvizhenii
kosmicheskih tel v central'nom pole
tyagoteniya;
- o zakonah dvizheniya kosmicheskih tel v
central'nom pole tyagoteniya (zakonah
Keplera);
- o traektoriyah dvizheniya (orbitah)
kosmicheskih tel i ih osnovnyh
harakteristikah;
- o kosmicheskih skorostyah;
- ob astronomicheskoi edinice izmereniya
mezhplanetnyh rasstoyanii.
Vospitatel'nye: formirovanie nauchnogo mirovozzreniya v hode znakomstva s istoriei chelovecheskogo poznaniya i ob'yasneniya prichin nebesnyh yavlenii, obuslovlennyh dvizheniem kosmicheskih tel; politehnicheskoe i trudovoe vospitanie v hode izlozheniya materiala o prakticheskih sposobah primeneniya znanii nebesnoi mehaniki v kosmonavtike.
Razvivayushie: formirovanie umenii reshat' zadachi na primenenie zakonov dvizheniya kosmicheskih tel i formul kosmicheskih skorostei.
Ucheniki dolzhny znat':
- o nebesnoi mehanike (predmete
ee issledovanii, svyazi s drugimi naukami,
osnovnyh etapah istorii i uchenyh, vnesshih
naibol'shii vklad v razvitie nebesnoi
mehaniki);
- zakony dvizheniya kosmicheskih tel v
central'nyh polyah tyagoteniya Keplera;
- o svyazi mezhdu formoi orbity i
skorost'yu dvizheniya kosmicheskih tel;
- astronomicheskie velichiny: formy orbit
kosmicheskih tel; znacheniya I, II, III
kosmicheskih skorostei (dlya Zemli); znachenie
astronomicheskoi edinicy rasstoyanii.
Ucheniki dolzhny umet': reshat' zadachi na primenenie zakonov dvizheniya kosmicheskih tel dlya rascheta ih orbit i kosmicheskih skorostei.
Naglyadnye posobiya i demonstracii:
Fragmenty diafil'mov: "Vidimoe
dvizhenie nebesnyh svetil"; "Sovetskie
iskusstvennye sputniki Zemli"; "Elementy
mehaniki kosmicheskih poletov".
Fragmenty kinofil'mov: "Petlya Marsa";
"Vsemirnoe tyagotenie"; "Uspehi SSSR
v osvoenii kosmosa"; "Kosmicheskie
polety"; "Planetnaya sistema"; "Dvizhenie
komety vokrug Solnca".
Tablicy: "Solnechnaya sistema"; "Kosmicheskie
polety".
Pribory i instrumenty: demonstracionnaya
model' planetnoi sistemy; pribor dlya
demonstracii dvizheniya ISZ.
Zadanie na dom:
1) Izuchit' materiala uchebnikov:
- B.A. Voroncov-Vel'yaminova: §§ 11, 13 (1,
2); uprazhneniya: 8 (1-3).
- E.P. Levitana: § 9 (2); voprosy-zadaniya.
- A.V. Zasova, E.V. Kononovicha: § 9, 10, 11 (1);
uprazhneniya 9.4 (2, 3), 9.5 (2, 4)
2) Vypolnit' zadaniya iz sbornika zadach Voroncova-Vel'yaminova B.A. [28]: 158; 171; 172.
Plan uroka
|
Etapy uroka |
Soderzhanie |
Metody izlozheniya |
Vremya, min |
|
1 |
Aktualizaciya temy zanyatiya |
Frontal'nyi opros, beseda |
3-5 |
|
2 |
Povtorenie materiala o zakone Vsemirnogo tyagoteniya i istorii ego otkrytiya |
Beseda, lekciya |
7-10 |
|
3 |
Formirovanie ponyatii o dvizhenii kosmicheskih tel i zakonah Keplera |
Lekciya |
10-12 |
|
4 |
Formirovanie ponyatii o kosmicheskih skorostyah |
Lekciya |
7-10 |
|
5 |
Reshenie zadach |
Rabota u doski, samostoyatel'noe reshenie zadach v tetradi |
10-12 |
|
6 |
Obobshenie proidennogo materiala, podvedenie itogov uroka, domashnee zadanie |
3 |
|
Metodika izlozheniya materiala
1. V nachale uroka sleduet aktualizirovat' temu zanyatiya. V hode besedy, vyrastayushei iz frontal'nogo oprosa ob osnovnyh razdelah astronomii, osnovnyh etapah ee razvitiya, svyazi astronomii s drugimi naukami, uchashimsya rasskazyvaetsya o nebesnoi mehanike, ee predmete, metodah i instrumentah issledovanii, istorii vozniknoveniya i razvitiya nebesnoi mehaniki i ee svyazi s drugimi naukami (fizikoi i matematikoi). Izlagaemyi material baziruetsya na ranee izuchennyh svedeniyah i paragrafe "Istoriya astronomii".
Sleduet ob'yasnit' uchenikam, osnovnoe otlichie novogo razdela astronomii – nebesnoi mehaniki – ot astrometrii. Ranee oni izuchali vidimye nebesnye yavleniya i lish' opisatel'no ih prichiny – kosmicheskie yavleniya. Teper' v izuchenii kursa astronomii nastupaet novyi etap, svyazannyi s perehodom k podrobnomu rassmotreniyu fizicheskoi prirody samih kosmicheskih yavlenii.
Osnovoi problemnoi situacii stanovitsya neobhodimost' vyyasneniya zakonov dvizheniya kosmicheskih tel dlya ob'yasneniya svoistv i harakteristik izvestnyh nebesnyh yavlenii. Chto my dolzhny dlya etogo znat'? – sprashivaem shkol'nikov i oni opredelyayut krug neobhodimyh znanii po astronomii, fizike i matematike (v sluchae zatrudneniya uchitel' pomogaet im navodyashimi voprosami). Povtoryaetsya, aktualiziruetsya ranee proidennyi astronomicheskii material o konfiguraciyah i vidimom dvizhenii planet, strukture Solnechnoi sistemy; osnovnye zakony i ponyatiya kinematiki (svyazannye s opisaniem vrashatel'nogo dvizheniya tel) i dinamiki (zakony N'yutona).
2. Formirovanie ponyatii o zakonah dvizheniya kosmicheskih tel – zakonah Keplera mozhno osushestvit' raznymi variantami v neskol'ko etapov:
I variant – dlya "slabyh" ili "obychnyh" klassov i klassov s himiko-biologicheskoi ili gumanitarnoi orientaciei:
1. Izlozhenie istorii otkrytiya zakonov Keplera i Vsemirnogo tyagoteniya.
2. Vyvod zakonov Keplera "avtorskim sposobom", uproshennym i adaptirovannym k vospriyatiyu sovremennyh uchashihsya. Opredelenie zakonov Keplera v "istoricheski pervozdannom" vide s ogovorkoi ih empiricheskogo haraktera: podcherkivaetsya, chto I. Kepler lish' opisal harakter dvizheniya planet, no ne ob'yasnil ego prichin.
Zakony Keplera formuliruyutsya v predel'no uproshennoi forme:
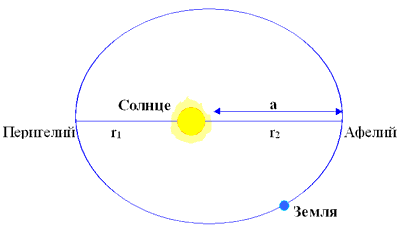
I. Vse planety Solnechnoi sistemy vrashayutsya vokrug Solnca po ellipticheskim orbitam, v odnom iz fokusov kotoryh nahoditsya Solnce.
II. Radius-vektor planety za odinakovye promezhutki vremeni opisyvaet ravnye ploshadi: skorost' dvizheniya planet maksimal'na v perigelii i minimal'na v afelii.
III. Kvadraty periodov obrasheniya
planet vokrug Solnca sootnosyatsya mezhdu
soboi, kak kuby ih srednih rasstoyanii ot
Solnca: 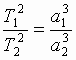
3. Izlozhenie istorii otkrytiya zakona Vsemirnogo tyagoteniya iz zakonov Keplera i zakonov mehaniki (s vyvodom ili bez nego).
Uproshennyi vyvod zakona Vsemirnogo tyagoteniya opisan v uchebnike fiziki dlya X klassov fiziko-matematicheskih shkol pod redakciei A.A. Pinskogo [49, s. 22]:
Esli planety dvizhutsya po pochti
krugovym orbitam, ih centrostremitel'nye
uskoreniya ravny: 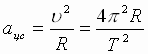 (1),
gde T – period obrasheniya planety
vokrug Solnca, R - radius orbity planety.
Iz III zakona Keplera
(1),
gde T – period obrasheniya planety
vokrug Solnca, R - radius orbity planety.
Iz III zakona Keplera 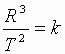 ili
ili 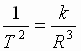 (2).
Sledovatel'no, uskorenie lyuboi planety
nezavisimo ot ee massy obratno
proporcional'no kvadratu radiusa ee orbity:
(2).
Sledovatel'no, uskorenie lyuboi planety
nezavisimo ot ee massy obratno
proporcional'no kvadratu radiusa ee orbity:
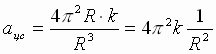 (3).
(3).
Soglasno II zakonu N'yutona, sila F,
soobshayushaya planete eto uskorenie, ravna: 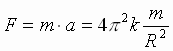 (4):
sila, deistvuyushaya na lyubuyu planetu, pryamo
proporcional'na masse planety i obratno
proporcional'na kvadratu rasstoyaniya ot nee
do Solnca.
(4):
sila, deistvuyushaya na lyubuyu planetu, pryamo
proporcional'na masse planety i obratno
proporcional'na kvadratu rasstoyaniya ot nee
do Solnca.
Soglasno III zakonu N'yutona, sila F¢
, deistvuyushaya na planetu so storony
Solnca, ravna ei po modulyu, protivopolozhna
po napravleniyu i ravna: 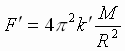 (5),
gde M – massa Solnca.
(5),
gde M – massa Solnca.
Poskol'ku F = F¢
, 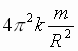 =
=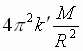 .
Oboznachim
.
Oboznachim 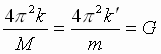 (6),
gde G – postoyannaya velichina. Togda
(6),
gde G – postoyannaya velichina. Togda ![]() (7)
i vyrazhenie (4) mozhno zapisat' v vide
izvestnoi nam formuly zakona Vsemirnogo
tyagoteniya:
(7)
i vyrazhenie (4) mozhno zapisat' v vide
izvestnoi nam formuly zakona Vsemirnogo
tyagoteniya: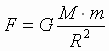 (8): Sila tyagoteniya mezhdu Solncem i
planetoi proporcional'na proizvedeniyu ih
mass i obratno proporcional'na kvadratu
rasstoyaniya mezhdu nimi.
(8): Sila tyagoteniya mezhdu Solncem i
planetoi proporcional'na proizvedeniyu ih
mass i obratno proporcional'na kvadratu
rasstoyaniya mezhdu nimi.
4. Sovremennaya formulirovka zakonov dvizheniya kosmicheskih tel v central'nom pole tyagoteniya i opredelenie ponyatii, svyazannyh s opisaniem dvizheniya kosmicheskih tel i harakteristikami orbit (sm.).
II variant dlya "sil'nyh " i fiziko-matematicheskih klassov:
1. Izlozhenie istorii otkrytiya zakonov Keplera i zakona Vsemirnogo tyagoteniya. Opredelenie zakonov Keplera i zakona Vsemirnogo tyagoteniya.
2. Vyvod zakonov Keplera na osnove zakona Vsemirnogo tyagoteniya i zakonov mehaniki.
|
|
|
|
Ris. 58 Zakony Keplera |
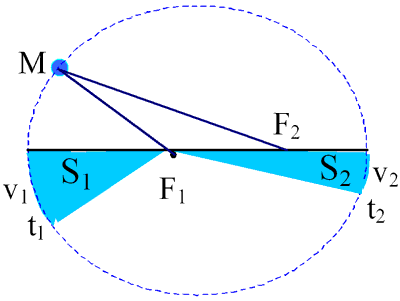
Ris.59 Vtoroi zakon Keplera |
A.I. Fetisov predlagaet kachestvennyi vyvod I i II zakonov Keplera, povtoryayushii rassuzhdeniya avtora otkrytiya:
Kepleru byli izvestny: koordinaty planety (Marsa) na nebesnoi sfere s tochnost'yu do 2¢ po dannym nablyudenii T. Brage; otnositel'nye rasstoyaniya planet ot Solnca; sinodicheskie i sidericheskie periody obrasheniya planet. Dalee on mog rassuzhdat':
|
|
|
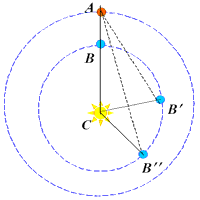
Ris. 60 |
Izvestno polozhenie Marsa vo vremya protivostoyaniya (ris. 60). V treugol'nike AVS bukva A oboznachaet polozhenie Marsa, V - Zemli, S – Solnca. Cherez promezhutok vremeni, ravnyi sidericheskomu periodu obrasheniya Marsa (687d) planeta vernetsya v tochku M, a Zemlya za eto vremya peremestitsya v tochku V¢ . Poskol'ku uglovye skorosti dvizheniya Zemli v techenie goda izvestny (oni ravny uglovym skorostyam vidimogo dvizheniya Solnca po ekliptike), mozhno vychislit' ugol ASV¢ . Opredeliv koordinaty Marsa i Solnca v moment prohozhdeniya Zemlei cherez tochku V¢ , my mozhem, znaya v treugol'nike 2 ugla, po teoreme sinusov rasschitat' otnoshenie storony SV¢ k AS. Eshe cherez odin oborot Marsa Zemlya pridet v polozhenie V" i mozhno budet opredelit' otnoshenie SV" k tomu zhe otrezku AS i t.d. Takim obrazom, tochka za tochkoi mozhno poluchit' predstavlenie ob istinnoi forme orbity Zemli, ustanovit, chto ona yavlyaetsya ellipsom, v fokuse kotorogo nahoditsya Solnce (I zakon Keplera); chto v blizhaishei k Solncu tochke svoei orbity Zemlya dvizhetsya naibolee bystro, a v samoi dalekoi – naibolee medlenno (II zakon Keplera).
Bolee slozhnyi (no i bolee podrobnyi, kolichestvennyi) vyvod zakonov Keplera mozhno osushestvit' soglasno metodike Yu.I. Sokolovskogo [271]. Izlozhenie materiala udobnee nachinat' s vyvoda II zakona Keplera kak naglyadno-geometricheskogo istolkovaniya zakona sohraneniya momenta impul'sa.
Sila gravitacionnogo prityazheniya planety Solncem napravlena k ee centru, ee moment otnositel'no lyuboi osi, prohodyashei cherez centr, raven nulyu. Moment impul'sa planety N ostaetsya neizmennym:
N = m× u ^ × r = m× u × h = const, gde m – massa planety, r – rasstoyanie ot Solnca, u - skorost' planety; u ^ - sostavlyayushaya etoi skorosti, perpendikulyarnaya napravleniyu na Solnce; h – dlina perpendikulyara, opushennogo iz centra Solnca na vektor skorosti ili ego prodolzhenie. Pri neizmennoi masse planety iz sohraneniya momenta impul'sa sleduet postoyanstvo proizvedeniya momenta skorosti u × h: u × h = N/m = const. Pust' u × h = n.
|
|
|
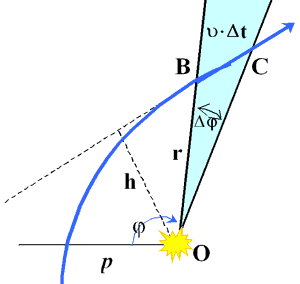
Ris. 61 |
Za promezhutok vremeni D
t planeta peremeshaetsya vdol' orbity na
rasstoyanie VS = u ×
D t. Radius-vektor OV
kak by "ometaet" sektor orbity VOS
– treugol'nik s neskol'ko iskrivlennym
osnovaniem VS = u ×
D t i vysotoi h. Ego
ploshad':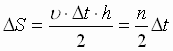 .
Sledovatel'no, otnoshenie
.
Sledovatel'no, otnoshenie 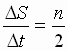 dlya dannoi orbity postoyanno. Ono
harakterizuet bystrotu "ometaniya"
ploshadi, chislenno ravno ploshadi sektora,
"ometaemogo" radius-vektorom za
edinicu vremeni i nazyvaetsya sektoral'noi
skorost'yu (ris. 61).
dlya dannoi orbity postoyanno. Ono
harakterizuet bystrotu "ometaniya"
ploshadi, chislenno ravno ploshadi sektora,
"ometaemogo" radius-vektorom za
edinicu vremeni i nazyvaetsya sektoral'noi
skorost'yu (ris. 61).
Dlya vychisleniya ploshadi S,
"ometaemoi" za promezhutok vremeni t,
razob'em ego na elementarnye promezhutki D
t1, D t2, D
t3 … Togda: 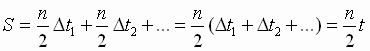 ,
otkuda sleduet formulirovka II zakona
Keplera: "Za lyubye ravnye promezhutki
vremeni radius-vektor planety "ometaet"
ravnye ploshadi".
,
otkuda sleduet formulirovka II zakona
Keplera: "Za lyubye ravnye promezhutki
vremeni radius-vektor planety "ometaet"
ravnye ploshadi".
Uchenikam napominayut opredelenie ellipsa i sposob ego prakticheskogo postroeniya.
Ellips - krivaya II poryadka, dlya
lyuboi tochki kotoroi summa rasstoyanii ot
dvuh tochek, nazyvaemyh fokusami ellipsa,
postoyanna (ris. 58). Stepen'
vytyanutosti ellipsa harakterizuetsya ekscentrisitetom
e, 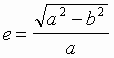 ,
gde a i b - poluosi ellipticheskoi
orbity. Pri sovpadenii fokusov s centrom (e
= 0) ellips prevrashaetsya v okruzhnost'; pri e
= 1 stanovitsya paraboloi; pri e > 1 -
giperboloi.
,
gde a i b - poluosi ellipticheskoi
orbity. Pri sovpadenii fokusov s centrom (e
= 0) ellips prevrashaetsya v okruzhnost'; pri e
= 1 stanovitsya paraboloi; pri e > 1 -
giperboloi.
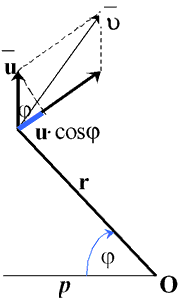
Vyvod I zakona Keplera: Dvizhenie
planet udobno opisyvat' v polyarnoi sisteme
koordinat, nachalo kotoroi O
sovmesheno s Solncem: polozhenie planety
opredelyaetsya polyarnym rasstoyaniem r
i polyarnym uglom j (ris.
58). Rassmotrim orbity s odinakovymi
momentom skorosti n i sektoral'noi
skorost'yu 0,5n. Pri dvizhenii po lyuboi
iz nih planeta peresechet sektor VOS
s uglom D j pri
vershine i ploshad'yu D S = 0,5r2×
D j za
vremya: 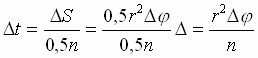 (1)
Uskorenie planety ac
opredelyaetsya prityazheniem Solnca; po zakonu
Vsemirnogo tyagoteniya:
(1)
Uskorenie planety ac
opredelyaetsya prityazheniem Solnca; po zakonu
Vsemirnogo tyagoteniya: 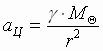 (2).
Iz (1), (2) opredelyaetsya modul' izmeneniya
vektora skorosti planety za vremya
peresecheniya rassmatrivaemogo sektora:
(2).
Iz (1), (2) opredelyaetsya modul' izmeneniya
vektora skorosti planety za vremya
peresecheniya rassmatrivaemogo sektora: 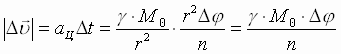 .
Modul' izmeneniya vektora skorosti
opredelyaetsya momentom skorosti n i
uglom D j pri
vershine sektora i ne zavisit ot rasstoyaniya
planety ot Solnca, t.k. oslablenie
gravitacii s udaleniem ot Solnca
kompensiruetsya uvelicheniem dlitel'nosti
ee vozdeistviya.
.
Modul' izmeneniya vektora skorosti
opredelyaetsya momentom skorosti n i
uglom D j pri
vershine sektora i ne zavisit ot rasstoyaniya
planety ot Solnca, t.k. oslablenie
gravitacii s udaleniem ot Solnca
kompensiruetsya uvelicheniem dlitel'nosti
ee vozdeistviya.
Pust' radius krugovoi orbity rk,
a modul' lineinoi skorosti planety u
k. Vektor etoi skorosti menyaetsya pri
dvizhenii tol'ko po napravleniyu, ostavayas'
perpendikulyarnym radiusu, tak chto moment
skorosti n = rkuk.
Radius krugovoi orbity opredelyaetsya,
otozhdestvlyaya uskorenie planety s
centrostremitel'nym uskoreniem: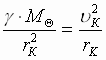 , no
, no 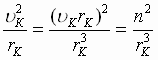 (3) Þ
(3) Þ
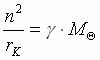 (4) i
(4) i 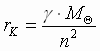 .
Pri dvizhenii planety s tem zhe momentom
skorosti po lyuboi drugoi orbite vektor ee
lineinoi skorosti budet inym, no izmenyat'sya
pri prohozhdenii sektora s uglom D
j budet na tu zhe velichinu D`
u , chto i pri dvizhenii po
okruzhnosti. Znachit, vektory ` u
i ` u k mogut
otlichat'sya drug ot druga tol'ko na
postoyannoe po modulyu i po napravleniyu
vektornoe slagaemoe u: ` u
=` u k +`
u. Napravim polyarnuyu os' OR
perpendikulyarno vektoru u tak, chtoby v
tochke R vektory` u
k i` u sovpadali po
napravleniyu. V proizvol'nom polozhenii
planety ee lineinaya skorost'`
u geometricheski skladyvaetsya
iz skorosti` u k
i postoyannogo vektora` u.
Moment skorosti raven summe momentov ee
sostavlyayushih: n = r× u
k + r× u×
cosj Þ
.
Pri dvizhenii planety s tem zhe momentom
skorosti po lyuboi drugoi orbite vektor ee
lineinoi skorosti budet inym, no izmenyat'sya
pri prohozhdenii sektora s uglom D
j budet na tu zhe velichinu D`
u , chto i pri dvizhenii po
okruzhnosti. Znachit, vektory ` u
i ` u k mogut
otlichat'sya drug ot druga tol'ko na
postoyannoe po modulyu i po napravleniyu
vektornoe slagaemoe u: ` u
=` u k +`
u. Napravim polyarnuyu os' OR
perpendikulyarno vektoru u tak, chtoby v
tochke R vektory` u
k i` u sovpadali po
napravleniyu. V proizvol'nom polozhenii
planety ee lineinaya skorost'`
u geometricheski skladyvaetsya
iz skorosti` u k
i postoyannogo vektora` u.
Moment skorosti raven summe momentov ee
sostavlyayushih: n = r× u
k + r× u×
cosj Þ
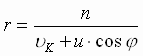 ili
ili 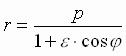 (5), gde
(5), gde 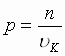 i
i 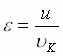 –
postoyannye velichiny.
–
postoyannye velichiny.
Vyrazhenie (5) polnost'yu opredelyaet formu orbity. Pri e < 1 ono predstavlyaet soboi uravnenie ellipsa s fokal'nym parametrom r i ekscentrisitetom e , odin iz fokusov kotorogo sovpadaet s centrom koordinat – centrom Solnca. Pri e = 1 uravnenie (5) opisyvaet parabolu; pri e > 1 – giperbolu. Formuliruem I zakona Keplera: "Planetnye tela dvizhutsya po orbitam, predstavlyayushim soboi krivye II poryadka, v odnom iz fokusov kotoryh nahoditsya centr mass sistemy".
Pri j = 0 rasstoyanie
planety ot Solnca minimal'no i ravno 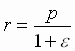 ;
v etoi tochke perigeliya skorost' planety
maksimal'na i ravna` u
k +` u. Pri j
= p , v afelii, modul' skorosti
imeet minimal'noe znachenie` u
k -` u. Pri j
= ± p /2
rasstoyanie ot Solnca ravno r, chem
raskryvaetsya geometricheskii smysl
fokal'nogo parametra. Pri e = 0
rasstoyanie ot Solnca ravno r pri
lyubom j , t.e. planeta dvizhetsya
po okruzhnosti. Eto imeet mesto i pri u
= 0, t.e. pri nachal'noi i neizmennoi po modulyu
skorosti planety u = u
k + u = u k. T.o.
parametr r est' radius krugovoi
orbity s dannym momentom impul'sa, a
skorost' u k –
krugovaya ili I kosmicheskaya skorost' na
rasstoyanii rk = r ot
Solnca.
;
v etoi tochke perigeliya skorost' planety
maksimal'na i ravna` u
k +` u. Pri j
= p , v afelii, modul' skorosti
imeet minimal'noe znachenie` u
k -` u. Pri j
= ± p /2
rasstoyanie ot Solnca ravno r, chem
raskryvaetsya geometricheskii smysl
fokal'nogo parametra. Pri e = 0
rasstoyanie ot Solnca ravno r pri
lyubom j , t.e. planeta dvizhetsya
po okruzhnosti. Eto imeet mesto i pri u
= 0, t.e. pri nachal'noi i neizmennoi po modulyu
skorosti planety u = u
k + u = u k. T.o.
parametr r est' radius krugovoi
orbity s dannym momentom impul'sa, a
skorost' u k –
krugovaya ili I kosmicheskaya skorost' na
rasstoyanii rk = r ot
Solnca.
|
|
|
Ris.62 |
Orbita imeet parabolicheskuyu formu
pri e = 1, u = u
k. V sootvetstvie s (5) pri e
= 1 i j = 0 perigelii
parabolicheskoi orbity nahoditsya na
rasstoyanii r/2 ot Solnca. Chtoby telo
dvigalos' po parabole, nado soobshit' emu v
perigelii nachal'nuyu skorost': u
= u k + u = u
k + u k = 2u
k – parabolicheskuyu ili II
kosmicheskuyu. Krugovaya (I kosmicheskaya)
skorost' v etoi tochke ravna ![]() .
T. k. cherez u k byla
oboznachena krugovaya skorost' dlya vdvoe
bol'shego udaleniya ot Solnca rk = p,
a po (4) znachenie krugovoi skorosti obratno
proporcional'no
.
T. k. cherez u k byla
oboznachena krugovaya skorost' dlya vdvoe
bol'shego udaleniya ot Solnca rk = p,
a po (4) znachenie krugovoi skorosti obratno
proporcional'no ![]() ,
parabolicheskaya u P
skorost' ravna
,
parabolicheskaya u P
skorost' ravna ![]() ,
t.e. v
,
t.e. v ![]() raz prevyshaet
krugovuyu dlya toi zhe tochki.
raz prevyshaet
krugovuyu dlya toi zhe tochki.
Vyvod III zakona Keplera: Blagodarya postoyanstvu sektoral'noi skorosti period obrasheniya planety T opredelyaetsya deleniem "ometaemoi" za 1 oborot ploshadi ellipsa S na sektoral'nuyu skorost' n/2. T.k. ploshad' ellipsa S = p × a× b, gde a i b – bol'shaya i malaya poluosi.
 (6).
T.k. dlya ellipsa b2 = p×
a,
(6).
T.k. dlya ellipsa b2 = p×
a,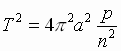 (7). Uchityvaya, chto p = rk i (4),
poluchim
(7). Uchityvaya, chto p = rk i (4),
poluchim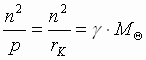 .
Togda formula (7) zapishetsya:
.
Togda formula (7) zapishetsya: 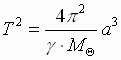 .
.
V etom vyrazhenii 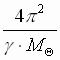 –
velichina postoyannaya (
–
velichina postoyannaya (![]() odinakova
dlya vseh planet Solnechnoi sistemy), poetomu
dlya lyubyh dvuh ee planet:
odinakova
dlya vseh planet Solnechnoi sistemy), poetomu
dlya lyubyh dvuh ee planet: 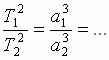 Formuliruem III zakon Keplera : "Kvadraty
periodov obrasheniya dvuh planet sootnosyatsya
kak kuby bol'shih poluosei ih orbit".
Formuliruem III zakon Keplera : "Kvadraty
periodov obrasheniya dvuh planet sootnosyatsya
kak kuby bol'shih poluosei ih orbit".
V posobii [167?] predlagaetsya sleduyushii vyvod utochnennogo III zakona Keplera dlya krugovogo dvizheniya:
Soglasno zakonu Vsemirnogo
tyagoteniya, uskoreniya dvuh vzaimno
prityagivayushihsya i obrashayushihsya vokrug
obshego centra mass kosmicheskih tel ravny: 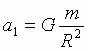 ,
,
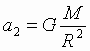 (1), gde M
i m – massy tel, R - rasstoyanie
mezhdu ih centrami.
(1), gde M
i m – massy tel, R - rasstoyanie
mezhdu ih centrami.
Uglovaya skorost' ih obrasheniya
vokrug centra mass ravna 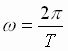 ,
gde T – period obrasheniya. Togda
centrostremitel'noe uskorenie tel:
,
gde T – period obrasheniya. Togda
centrostremitel'noe uskorenie tel: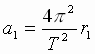 ,
,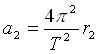 (2), gde
r1 i r2 - rasstoyaniya tel ot
centra mass sistemy.
(2), gde
r1 i r2 - rasstoyaniya tel ot
centra mass sistemy.
Priravnivaya vyrazheniya (1) i (2),
poluchim: 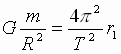 ,
, 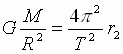 (3).
(3).
Skladyvaya pochlenno vyrazheniya (3),
poluchim: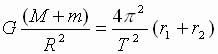 Þ
Þ 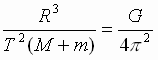 (4).
(4).
V pravoi chasti vyrazheniya (4) nahodyatsya lish' postoyannye velichiny, otkuda sleduet ego spravedlivost' dlya lyuboi sistemy dvuh gravitacionno vzaimodeistvuyushih tel. Dlya dvuh kosmicheskih sistem eto vyrazhenie zapishetsya v vide utochnennogo III zakona Keplera:
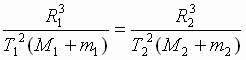 Þ
Þ
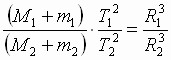
3. Polnaya formulirovka zakonov dvizheniya kosmicheskih tel v central'nom pole tyagoteniya i opredelenie ponyatii, svyazannyh s opisaniem dvizheniya kosmicheskih tel i harakteristikami orbit:
|
|
|
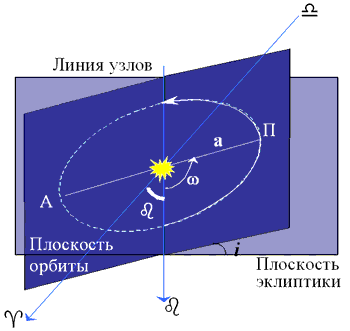
Ris. 63. Elementy orbit |
Osnovnye harakteristiki dvizheniya kosmicheskogo tela v predelah Solnechnoi sistemy – nazyvayutsya elementami orbity i opredelyayutsya otnositel'no ploskosti ekliptiki (ris. 63).
Ugol i mezhdu ploskost'yu orbity i ekliptikoi nazyvaetsya ee nakloneniem: pri 0œ £ i < 90œ kosmicheskoe telo dvizhetsya vokrug Solnca v pryamom napravlenii (kak Zemlya); pri 90œ £ i < 180œ – v obratnom napravlenii.
Tochki, v kotoryh orbita kosmicheskogo tela peresekaetsya s ploskost'yu ekliptiki, nazyvayutsya uzlami ego orbity: voshodyashim uzlom v napravlenii severnogo polyusa ekliptiki i nishodyashim uzlom v napravlenii yuzhnogo polyusa ekliptiki.
Ugol b mezhdu centrom Solnca, voshodyashim uzlom orbity i tochkoi vesennego ravnodenstviya nazyvaetsya geliocentricheskoi dolgotoi voshodyashego uzla i vmeste s nakloneniem opredelyaet prostranstvennoe polozhenie ploskosti orbity kosmicheskogo tela.
Ugol w mezhdu centrom Solnca, voshodyashim uzlom orbity i tochku perigeliya nazyvaetsya uglovym rasstoyaniem perigeliya ot uzla, otschityvaetsya v ploskosti orbity v napravlenii dvizheniya kosmicheskogo tela i opredelyaet polozhenie orbity v ee ploskosti.
Moment prohozhdeniya perigeliya t0 opredelyaet polozhenie kosmicheskogo tela na orbite v dannoe vremya.
Bol'shaya poluos' orbity a
yavlyaetsya srednim rasstoyaniem kosmicheskogo
tela ot Solnca i opredelyaet razmery ego
orbity: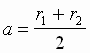 ,
, ![]() gde r1 - rasstoyanie kosmicheskogo
tela ot Solnca v perigelii, r2 - v
afelii.
gde r1 - rasstoyanie kosmicheskogo
tela ot Solnca v perigelii, r2 - v
afelii.
Bol'shaya poluos' zemnoi orbity prinyata za astronomicheskuyu edinicu rasstoyanii: aÅ = 1 a. e. = 149000000000 m.
Opredeleniem polozhenii ob'ektov Solnechnoi sistemy na nebesnoi sfere po elementam ih orbit (vychisleniem efemerid kosmicheskih tel) i opredeleniem elementov orbit kosmicheskih tel na osnove nablyudenii ih vidimogo dvizheniya zanimaetsya teoreticheskaya astronomiya.
Dlya opredeleniya harakteristik orbity kosmicheskogo tela neobhodimo provesti ne menee 3 izmerenii ekvatorial'nyh koordinat svetila na nebesnoi sfere (tochnost' vychislenii povyshaetsya pri uvelichenii kolichestva nablyudenii). Na osnove dannyh nablyudenii sostavlyaetsya sistema iz 6 uravnenii, kazhdoe iz kotoryh soderzhit izvestnye ekvatorial'nye koordinaty svetila i v kachestve neizvestnoi velichiny – odin iz elementov orbity kosmicheskogo tela. Klassicheskii sposob resheniya zadachi byl metod "naimen'shih kvadratov"; v nastoyashee vremya dlya raschetov shiroko primenyayutsya EVM.
I zakon Keplera:
Traektorii dvizheniya nebesnyh tel v central'nom pole tyagoteniya predstavlyayut soboi konicheskoe sechenie (krivuyu II poryadka): ellips, okruzhnost', parabolu ili giperbolu, v odnom iz fokusov kotoroi nahoditsya centr mass sistemy.
orbity planet Solnechnoi sistemy imeyut formu ellipsa, v odnom iz fokusov kotorogo nahoditsya Solnce. Massa Solnca v 750 raz bol'she massy vseh ostal'nyh tel Solnechnoi sistemy, poetomu centr mass Solnechnoi sistemy nahoditsya vnutri Solnca, pochti sovpadaya s ego geometricheskim centrom. Ellipticheskie orbity imeyut sputniki planet, v tom chisle ISZ, asteroidy i chast' komet. Ekscentrisitet e planetnyh orbit ochen' mal (eÅ = 0,017). Ekscentrisitety orbit asteroidov znachitel'no bol'she, mnogie komety imeyut parabolicheskie i giperbolicheskie orbity.
Pericentrom nazyvaetsya blizhaishaya k centru mass sistemy tochka orbity nebesnogo tela; apocentrom - naibolee udalennaya. Dlya orbit nebesnyh tel, vrashayushihsya vokrug Solnca, oni budut sootvetstvenno nazyvat'sya perigeliem i afeliem; dlya orbit tel, vrashayushihsya vokrug Zemli - perigeem i apogeem i t. d.
|
|
|
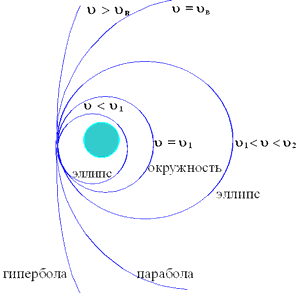
Ris.64 Kosmicheskie
skorosti. Zavisimost' |
Orbita nebesnogo tela zavisit ot ego skorosti v dannoi tochke prostranstva (ris. 64).
I kosmicheskaya skorost' yavlyaetsya
skorost'yu krugovogo dvizheniya: 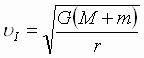 .
.
Dlya ISZ, zapuskaemyh na okolozemnye nizkie orbity (h = 200 km), u I =7,78 km/s.
II kosmicheskaya skorost' -
skorost' parabolicheskogo dvizheniya: 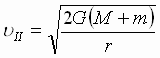 .
.
Dlya startuyushih s Zemli avtomaticheskih mezhplanetnyh stancii u II = 11,02 km/s.
Pri u I < u
< u II telo dvizhetsya po
ellipticheskoi orbite. Pri u
< u I telo takzhe
dvizhetsya po ellipticheskoi orbite, kotoraya
za isklyucheniem tochki apocentra budet
celikom lezhat' vnutri krugovoi orbity.
Takie traektorii poleta zemnyh kosmicheskih
letatel'nyh apparatov (KLA) nazyvayutsya
ballisticheskimi. Period vrasheniya nebesnyh
tel vokrug centra mass mozhno opredelit' po
formule: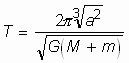 .
.
Pri u > u II traektoriya dvizheniya nebesnogo tela predstavlyaet soboi giperbolu.
Skorost', s kotoroi zapushennyi s Zemli KLA pokinet predely Solnechnoi sistemy, nazyvayut inogda tret'ei kosmicheskoi skorost'yu. Ona ravna summe skorostei dvizheniya Zemli vokrug Solnca i II kosmicheskoi skorosti KLA otnositel'no Zemli, u III = 42 km/s.
II zakon Keplera:
Pryamaya, soedinyayushaya nebesnoe telo s centrom mass, opisyvaet ravnye ploshadi v ravnye promezhutki vremeni, to est' ploshad', opisannaya radius-vektorom tela, proporcional'na vremeni, v techenie kotorogo ona opisana: pri t1 = t2, S1 = S2, u 1¹ u 2 (u 1>u 2) (ris. 59)
Tak kak za odno i to zhe vremya
nebesnoe telo prohodit raznye po
protyazhennosti uchastki orbity, ego dvizhenie
budet neravnomernym. Nebesnye tela vblizi
pericentra imeyut skorost' bol'shuyu, chem
vblizi apocentra: 
III zakon Keplera:
Proizvedenie summ mass nebesnyh tel i ih sputnikov s kvadratami ih sidericheskih periodov obrashenie otnosyatsya kak kuby bol'shih poluosei ih orbit:
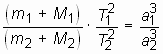 ,
gde M1 i M2 - massy
nebesnyh tel, m1 i m2 -
sootvetstvenno massy ih sputnikov, a1
i a2 - bol'shie poluosi ih orbit, T1
i T2 - sidericheskie periody
obrasheniya.
,
gde M1 i M2 - massy
nebesnyh tel, m1 i m2 -
sootvetstvenno massy ih sputnikov, a1
i a2 - bol'shie poluosi ih orbit, T1
i T2 - sidericheskie periody
obrasheniya.
Ucheniki dolzhny ponyat', chto zakon Keplera svyazyvaet harakteristiki dvizheniya komponentov lyubyh proizvol'nyh i nezavisimyh kosmicheskie sistem.
Izuchennyi material zakreplyaetsya v hode resheniya zadach.
Uprazhnenie 7:
1. K Zemle ili k Solncu sil'nee prityagivayutsya: a) ISZ; b) Luna [Otvet: FT¤ » 2,5FTÅ ].
2. Pochemu Solnce ne mozhet otorvat' Lunu ot Zemli?
3. Zadacha iz stat'i V.B. Drozdova [55]: Kakova dolzhna byt' minimal'naya skorost' zhyul'-vernovskogo snaryada, chtoby on popal v Lunu? Kakuyu skorost' on budet imet' u ee poverhnosti? [Otvet: 11,1 km/s; 2,3 km/s].
4. Kakova prodolzhitel'nost' sidericheskogo perioda vrasheniya Yupitera vokrug Solnca, esli on v 5 raz dal'she ot Solnca, nezheli Zemlya? Cherez kakie promezhutki vremeni povtoryayutsya ego protivostoyaniya?
5. Opredelite periody obrasheniya ISZ, dvigayushihsya po orbitam 1, 2 i 3 vokrug Zemli na ris. 64. Radius Zemli 6370 km.
6. Kakuyu skorost' dolzhna imet' na starte s poverhnosti Luny (Marsa) raketa, dostavlyayushaya na Zemlyu obrazcy grunta?
| << Predydushaya |
|
Publikacii s klyuchevymi slovami:
metodika prepodavaniya - prepodavanie astronomii - nablyudeniya - laboratornye raboty - prakticheskie raboty - uchebnaya programma - uchebnye posobiya - lekcii - pedagogicheskii eksperiment - didaktika - kontrol'nye raboty - zadacha
Publikacii so slovami: metodika prepodavaniya - prepodavanie astronomii - nablyudeniya - laboratornye raboty - prakticheskie raboty - uchebnaya programma - uchebnye posobiya - lekcii - pedagogicheskii eksperiment - didaktika - kontrol'nye raboty - zadacha | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |