Astronet > Dinamicheskie sistemy

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Dinamicheskie sistemy

V. S. Anishenko

Saratovskii gosudarstvennyi universitet im. N.G. Chernyshevskogo
Soderzhanie

Kolebatel'naya sistema nazyvaetsya lineinoi ili nelineinoi v zavisimosti ot togo, lineina ili nelineina opisyvayushaya ee sistema differencial'nyh uravnenii. Lineinye sistemy yavlyayutsya chastnym sluchaem nelineinyh. Odnako v silu principial'noi vazhnosti lineinyh sistem pri issledovanii voprosov ustoichivosti kolebanii, a takzhe vozmozhnosti ispol'zovaniya principa superpozicii reshenii takaya klassifikaciya opravdanna.

Dinamicheskie sistemy, modeliruemye konechnym chislom obyknovennyh differencial'nyh uravnenii, nazyvayut sosredotochennymi ili tochechnymi sistemami. Oni opisyvayutsya s pomosh'yu konechnomernogo fazovogo prostranstva i harakterizuyutsya konechnym chislom stepenei svobody. Odna i ta zhe sistema v razlichnyh usloviyah mozhet rassmatrivat'sya libo kak sosredotochennaya, libo kak raspredelennaya. Matematicheskie modeli raspredelennyh sistem — eto differencial'nye uravneniya v chastnyh proizvodnyh, integral'nye uravneniya ili obyknovennye uravneniya s zapazdyvayushim argumentom. Chislo stepenei svobody raspredelennoi sistemy beskonechno, i trebuetsya beskonechnoe chislo dannyh dlya opredeleniya ee sostoyaniya.

Po energeticheskomu priznaku dinamicheskie sistemy delyatsya na konservativnye i nekonservativnye. Konservativnye sistemy harakterizuyutsya neizmennym vo vremeni zapasom energii. V mehanike ih nazyvayut gamil'tonovymi. Dlya konservativnyh sistem s n stepenyami svobody opredelyaetsya gamil'tonian sistemy H(p, q), gde q_i — obobshennye koordinaty, p_i — obobshennye impul'sy sistemy, i = 1, 2, ..., n. Gamil'tonian polnost'yu harakterizuet dinamicheskuyu prirodu sistemy i s fizicheskoi tochki zreniya v bol'shinstve sluchaev predstavlyaet soboi ee polnuyu energiyu. Evolyuciya vo vremeni konservativnyh sistem opisyvaetsya uravneniyami mehaniki Gamil'tona

$$\dot q_i = \frac{\partial \bf H\rm (\bf p\rm , \bf q\rm )}{\partial p_i}$,$ $\dot p_i = -\frac{\partial \bf H \rm (\bf p\rm , \bf q\rm )}{\partial q_i}.$ (9)

Dinamicheskie sistemy s izmenyayushimsya vo vremeni zapasom energii nazyvayutsya nekonservativnymi. Sistemy, v kotoryh energiya umen'shaetsya vo vremeni iz-za treniya ili rasseyaniya, nazyvayutsya dissipativnymi. V sootvetstvii s etim sistemy, energiya kotoryh vo vremeni narastaet, nazyvayutsya sistemami s otricatel'nym treniem ili otricatel'noi dissipaciei. Takie sistemy mozhno rassmatrivat' kak dissipativnye pri smene napravleniya otscheta vremeni na protivopolozhnoe.

Dinamicheskie sistemy nazyvayutsya avtonomnymi, esli oni ne podverzheny deistviyu vneshnih sil, peremennyh vo vremeni. Uravneniya avtonomnyh sistem yavnoi zavisimosti ot vremeni ne soderzhat. Bol'shinstvo real'nyh kolebatel'nyh sistem v fizike, radiofizike, biologii, himii i drugih oblastyah znanii nekonservativny. Sredi nih vydelyaetsya osobyi klass avtokolebatel'nyh sistem, kotorye principial'no nekonservativny i nelineiny. Avtokolebatel'noi nazyvayut dinamicheskuyu sistemu, preobrazuyushuyu energiyu istochnika v energiyu nezatuhayushih kolebanii, prichem osnovnye harakteristiki kolebanii (amplituda, chastota, forma kolebanii i t.d.) opredelyayutsya parametrami sistemy i v opredelennyh predelah ne zavisyat ot vybora ishodnogo nachal'nogo sostoyaniya.

Fazovye portrety tipichnyh kolebatel'nyh sistem

Geometricheskoe predstavlenie kolebanii. Metod analiza kolebatel'nyh processov s pomosh'yu issledovaniya fazovyh traektorii dinamicheskoi sistemy byl vveden v teoriyu kolebanii L.I. Mandel'shtamom i A.A. Andronovym i s teh por stal privychnym pri issledovanii razlichnyh kolebatel'nyh yavlenii. Obsudim neskol'ko prostyh, no tipichnyh primerov predstavleniya dinamicheskih processov v vide traektorii izobrazhayushei tochki v fazovom prostranstve.

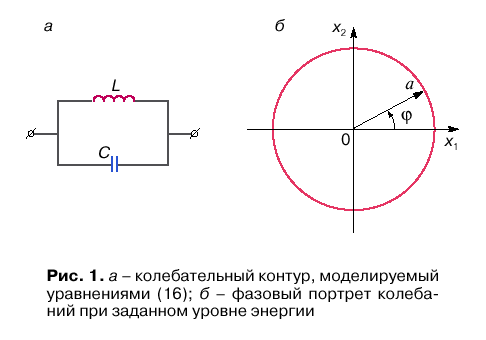
Konservativnyi oscillyator. Rassmotrim lineinyi oscillyator bez poter', uravneniya kotorogo mozhno sformulirovat' na primere kolebatel'nogo LC-kontura (ris. 1, a), predpolozhiv amplitudu kolebanii dostatochno maloi. Vybrav v kachestve peremennoi zaryad q na kondensatore, s pomosh'yu uravnenii Kirhgofa poluchim

$\ddot q +(LC)^{-1}q = 0.$ (10)

Domnozhiv (10) na $L\dot q$ , poluchaem

$\frac{d}{dt}\biggl( \frac{L\dot q^2}{2} + \frac{q^2}{2C} \biggr) = 0,$ (11)

to est' dlya lyubogo momenta vremeni vypolnyayutsya ravenstva

$E = E_L + E_C = const, E_L = \frac{L\dot q^2}{2}, E_C = \frac{q^2}{2C},$ (12)

otrazhayushie postoyanstvo vo vremeni polnoi energii oscillyatora (summy magnitnoi E_L i elektricheskoi E_C energii). V bolee udobnyh koordinatah uravneniya konservativnogo oscillyatora mozhno zapisat' sleduyushim obrazom, vvedya zamenu vremeni $\tau = t/\sqrt{LC}$ i oboznachaya dlya obshnosti q cherez x :

$\ddot x + x = 0,$ $\dot x^2 + x^2 = a^2,$ $a = const .$ (13)

Dlya fazovyh koordinat $x_1 = x$ i $x_2 = \dot x$ eti uravneniya preobrazuyutsya k vidu

$\dot x_1 = x_2,$ $\dot x_2 = - x_1,$ $x_1^2 + x_2^2 = a^2.$ (14)

Fazovyi portret sistemy predstavlyaet soboi okruzhnost' radiusa a s centrom v nachale koordinat. Tochka v fazovom prostranstve, v kotoroi vektor fazovoi skorosti obrashaetsya v nul', nazyvaetsya osoboi, i v dannom sluchae nul' koordinat est' osobaya tochka tipa centr.

Nalichie integrala dvizheniya u rassmatrivaemoi sistemy, otrazhayushee fakt sohraneniya energii (12), daet vozmozhnost' opisat' ee s pomosh'yu uravneniya 1-go poryadka. Deistvitel'no, opredeliv novuyu peremennuyu $\phi$ sootnosheniyami

$x_1 = a \sin \phi ,$ $x_2 = a \cos \phi ,$ (15)

poluchim uravneniya

$\dot \phi = 1,$ $\dot a = 0,$ (16)

kotorye i predstavlyayut zakon dvizheniya fazovoi tochki. Vo vremeni evolyucioniruet odna peremennaya $\phi$ , i fazovoe prostranstvo konservativnogo oscillyatora, takim obrazom, odnomerno. Garmonicheskim kolebaniyam oscillyatora otvechaet ravnomernoe dvizhenie izobrazhayushei tochki po okruzhnosti radiusa a, kak eto pokazano na ris. 1, b.

Esli konservativnaya sistema nelineina, to ee fazovyi portret uslozhnyaetsya. Proillyustriruem eto na primere uravneniya

$\ddot x + \sin x = 0.$ (17)

V fazovyh peremennyh $x_1 = x$ , $x_2 = \dot x$ eto uravnenie svoditsya k sleduyushim:

$\dot x_1 = x_2,$ $\dot x_2 = -\sin x_1.$ (18)

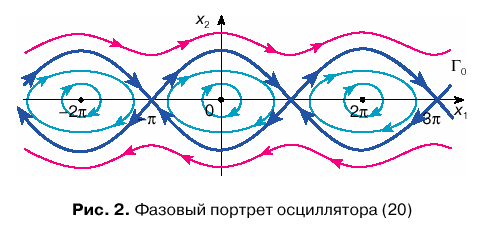
Sostoyaniya ravnovesiya nelineinogo mayatnika na fazovoi ploskosti raspolozheny vdol' osi x₁ (x₂ = 0) v tochkah $x_1 = 0, \pm \pi, \pm 2\pi, ...$ Sootvetstvuyushii fazovyi portret sistemy predstavlen na ris. 2. Vidno, chto osobye tochki $x_1 = 0, \pm 2\pi, \pm 4\pi, ...$ tipa centr, a $x_1 = 0, \pm \pi, \pm 3\pi, ...$ — neustoichivye tochki tipa sedlo.

Vblizi centrov fazovyi portret sootvetstvuet lineinomu oscillyatoru: traektorii predstavlyayut soboi zamknutye krivye, blizkie k okruzhnostyam, chto otvechaet po amplitude kolebaniyam, blizkim k garmonicheskim. Cherez neustoichivye tochki prohodyat osobye integral'nye krivye $\Gamma_0$ , nazyvaemye separatrisami. Oni razdelyayut fazovoe prostranstvo na oblasti s razlichnym povedeniem. S uvelicheniem energii mayatnika ego kolebaniya ot kvazigarmonicheskih vblizi tochek tipa centr evolyucioniruyut k nelineinym periodicheskim kolebaniyam vblizi separatris. Dal'neishee uvelichenie energii privedet k vrashatel'nomu dvizheniyu (dvizhenie vne separatris). Maleishie otkloneniya energii v tu ili inuyu storonu ot energii dvizheniya po separatrise privodyat k kachestvenno razlichnym tipam dvizheniya: kolebatel'nomu ili vrashatel'nomu.

Lineinyi oscillyator s zatuhaniem. Dissipaciya energii, obuslovlennaya nalichiem poter', okazyvaet principial'noe vliyanie na harakter dvizheniya sistemy. Naibolee prostye zakonomernosti proyavlyayutsya v sistemah s polnoi dissipaciei energii, kogda sily treniya deistvuyut po vsem stepenyam svobody, a postuplenie energii izvne otsutstvuet. Rassmotrim processy v lineinom dissipativnom oscillyatore, kogda sila treniya proporcional'na skorosti izmeneniya koordinaty. Primerom takoi sistemy sluzhit kolebatel'nyi kontur, soderzhashii aktivnoe soprotivlenie R. Uravnenie kontura

$L\ddot q + R\dot q + \frac{q}{C} = 0$ (19)

zamenoi peremennyh svoditsya k bezrazmernoi forme

$\ddot x + \delta \dot x +x = 0,$ $2\delta = R\sqrt{\frac{L}{C}},$ $\tau = \frac{t}{\sqrt{LC}}$ (20)

Pri d = 0 imeem konservativnyi lineinyi oscillyator, rassmotrennyi vyshe. Vvedenie malogo treniya kachestvenno menyaet fazovyi portret sistemy. Dlya 0 < d < 1 resheniem uravneniya (20) yavlyaetsya

$x = A \exp (-\delta t) \cos (\omega \tau + \psi),$ $\omega = (1 - \delta^2)^{1/2},$ (21)

gde A i $\psi$ — proizvol'nye postoyannye, opredelyaemye nachal'nymi usloviyami. Na fazovoi ploskosti dlya lyubyh nachal'nyh dannyh imeyut mesto skruchivayushiesya spirali, po kotorym fazovye tochki asimptoticheski priblizhayutsya k nachalu koordinat, harakterizuya zatuhayushii kolebatel'nyi process. Nul' koordinat yavlyaetsya osoboi tochkoi sistemy, kotoraya v sluchae d < 1 est' ustoichivyi fokus (ris. 3, a). Esli koefficient treniya d > 1, process v sisteme aperiodicheskii:

$x = A_1 \exp (\lambda_1 \tau) + A_2 \exp (\lambda_2 \tau),$
$\lambda_{1, 2} = [- \delta \pm (\delta^2 - 1)^{1/2}]/2$ (22)

i fazovye traektorii vyglyadyat kak semeistvo harakternyh krivyh, po kotorym, kak i v predydushem sluchae, izobrazhayushie tochki stremyatsya k nulyu koordinat (ris. 3, b). Osobaya tochka v ukazannyh usloviyah yavlyaetsya ustoichivym uzlom.

Itak, pri lyubyh znacheniyah fizicheskih parametrov sistemy, kogda $\delta > 0$ , dissipativnyi mayatnik harakterizuetsya edinstvennym global'no ustoichivym sostoyaniem ravnovesiya v nule fazovyh koordinat. Nezavisimo ot vybora nachal'nyh uslovii nablyudaetsya zatuhayushee kolebatel'noe ili aperiodicheskoe dvizhenie. Pri $t \to \infty$ lyubaya (!) izobrazhayushaya tochka stremitsya k nachalu koordinat v ustoichivyi fokus libo uzel.

Opisannoe svoistvo yavlyaetsya obshim dlya dinamicheskih sistem s polnoi dissipaciei energii. Polozheniya ravnovesiya tipa ustoichivogo fokusa ili uzla yavlyayutsya zdes' global'no prityagivayushimi v tom smysle, chto fazovye traektorii iz lyuboi tochki fazovogo prostranstva asimptoticheski k nim stremyatsya. Stacionarnye nezatuhayushie kolebaniya v lineinyh dissipativnyh sistemah okazyvayutsya nevozmozhnymi. S fizicheskoi tochki zreniya eto ponyatno — net uslovii podderzhaniya kolebanii. Energiya, rashoduemaya na preodolenie sil treniya, ne vospolnyaetsya.

Nazad | Vpered

Publikacii s klyuchevymi slovami: haos Publikacii so slovami: haos
Sm. takzhe: haos Vvedenie v fiziku otkrytyh sistem

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce