Astronet > Dinamicheskie sistemy

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Dinamicheskie sistemy

V. S. Anishenko

Saratovskii gosudarstvennyi universitet im. N.G. Chernyshevskogo
Soderzhanie

Vozmozhnost' sushestvovaniya periodicheskogo asimptoticheski ustoichivogo dvizheniya, izobrazhaemogo izolirovannoi zamknutoi traektoriei v fazovom prostranstve, k kotoroi so vremenem prityagivayutsya traektorii iz nekotoroi okrestnosti nezavisimo ot nachal'nyh uslovii, obespechivaetsya tol'ko v nelineinyh dissipativnyh sistemah. Etot tip dinamicheskih sistem nastol'ko vazhen pri izuchenii kolebatel'nyh processov, chto dlya ego vydeleniya A.A. Andronov predlozhil special'nyi termin — avtokolebatel'nye sistemy. Matematicheskim obrazom avtokolebanii sluzhit predel'nyi cikl Puankare — zamknutaya izolirovannaya traektoriya v fazovom prostranstve, otvechayushaya periodicheskomu dvizheniyu.

V kachestve primera dinamicheskoi sistemy s predel'nym ciklom Puankare rassmotrim klassicheskii nelineinyi oscillyator Van der Polya, uravnenie kolebanii kotorogo

$\ddot x - a(1 - bx^2)\dot x + x = 0.$ (23)

Parametr a, harakterizuyushii podkachku energii v sistemu ot vneshnego istochnika, yavlyaetsya sushestvennym parametrom oscillyatora i nazyvaetsya parametrom vozbuzhdeniya. Iz sravneniya uravnenii (23) i (20) sleduet, chto oscillyator Van der Polya opisyvaet bolee slozhnyi kolebatel'nyi kontur, harakter dissipacii v kotorom zavisit ot peremennoi x. V fazovyh koordinatah uravnenie kolebanii oscillyatora (23) predstavlyaetsya kak

$\dot x_1 = x_2,$
$\dot x_2 = a(1-bx_1^2)x_2 - x_1,$ (24)

prichem

$a(1-bx^2_1) \not\equiv 0.$ (25)

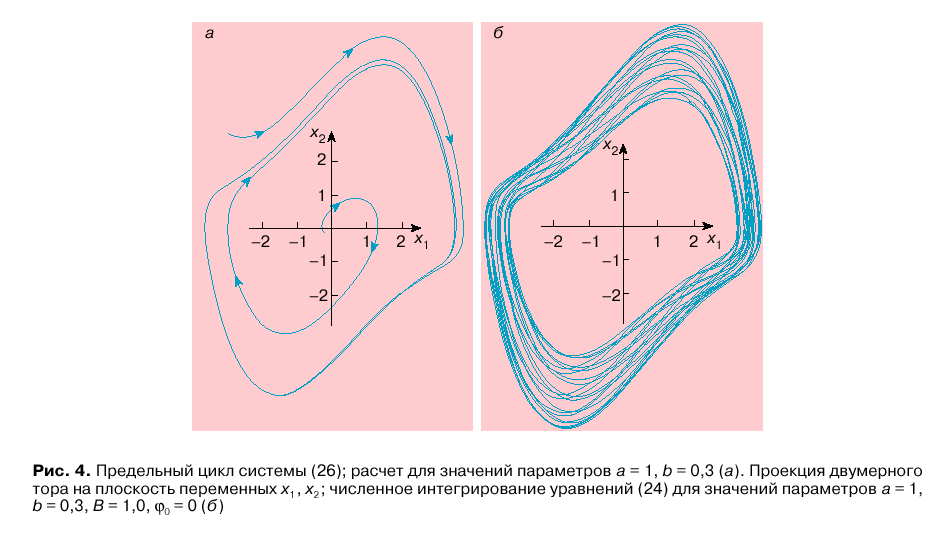
Analiticheski uravneniya (24) ne reshayutsya, i issledovaniya provodyatsya s ispol'zovaniem chislennyh metodov. V prakticheski vazhnom sluchae (a > 0, b > 0) uravneniya (24) imeyut edinstvennoe ustoichivoe reshenie v vide predel'nogo cikla $\Gamma$ , izobrazhennogo na ris. 4, a.

Polozhenie ravnovesiya v nachale koordinat, v kotorom vblizi nulya mozhno prenebrech' nelineinost'yu, yavlyaetsya neustoichivym fokusom. Traektorii iz okrestnosti sostoyaniya ravnovesiya asimptoticheski stremyatsya k predel'nomu ciklu. Kak pokazyvaet analiz, predel'nyi cikl yavlyaetsya ustoichivoi izolirovannoi strukturoi, prityagivayushei k sebe traektorii iz lyuboi tochki na fazovoi ploskosti.

Takim obrazom, v dinamicheskih sistemah s nelineinoi zavisimost'yu dissipacii energii ot peremennoi, sovershayushei kolebaniya, vpervye poyavlyaetsya principial'no novyi tip ustoichivogo predel'nogo mnozhestva fazovyh traektorii — predel'nyi cikl. Na predel'nom cikle za vremya perioda kolebanii doli rasseivaemoi i vnosimoi energii strogo kompensiruyutsya.

Nakonec, rassmotrim eshe odin sluchai tipichnoi struktury v fazovom prostranstve dinamicheskoi sistemy, voznikayushei, naprimer, pri periodicheskom vozmushenii sistemy s ustoichivym predel'nym ciklom. Dobavim v uravnenie (23) istochnik garmonicheskogo deistviya sravnitel'no maloi amplitudy B i chastoty p, kotoruyu schitaem racional'no ne svyazannoi s chastotoi periodicheskih kolebanii avtonomnogo oscillyatora:

$\ddot x - a(1-bx^2)\dot x + x = B\sin ( p\tau + \phi_0).$ (26)

Periodicheskaya modulyaciya predel'nogo cikla avtonomnoi sistemy privodit k tomu, chto fazovaya traektoriya s zadannoi chastotoi p vrashaetsya vokrug predel'nogo cikla i lezhit na dvumernoi poverhnosti, predstavlyayushei soboi poverhnost' tora. Analogichno sluchayu predel'nogo cikla eta poverhnost' budet ustoichivym predel'nym mnozhestvom, k kotoromu styagivayutsya so vremenem vse traektorii iz nekotoroi okrestnosti tora (kak iznutri nego, tak i snaruzhi!). Netrudno predstavit' sebe, chto minimal'naya razmernost' fazovogo prostranstva, v kotoroe mozhno vlozhit' dvumernyi tor, ravna trem. Na ris. 4, b pokazana proekciya na ploskost' peremennyh x₁, x₂ fazovoi traektorii na dvumernom tore, poluchennaya chislennym integrirovaniem sistemy (24).

Regulyarnye i strannye attraktory dinamicheskih sistem

Rassmotrennye primery illyustriruyut tipichnye predel'nye mnozhestva traektorii na fazovoi ploskosti: sostoyaniya ravnovesiya, periodicheskie dvizheniya i osobye traektorii tipa separatrisnyh konturov. Ukazannye predel'nye mnozhestva polnost'yu ischerpyvayut vozmozhnye situacii na fazovoi ploskosti. Im otvechayut tri razlichnyh tipa reshenii uravnenii.

Dvizheniya dissipativnyh sistem celesoobrazno razdelit' na dva klassa: klass perehodnyh, nestacionarnyh dvizhenii, otvechayushih relaksacii ot nachal'nogo k predel'nomu mnozhestvu sostoyanii, i klass ustanovivshihsya stacionarnyh dvizhenii, fazovye traektorii kotoryh celikom prinadlezhat predel'nym mnozhestvam. Vazhnymi s fizicheskoi tochki zreniya yavlyayutsya prityagivayushie predel'nye mnozhestva — attraktory. S techeniem vremeni proizvol'noe nachal'noe sostoyanie iz nekotoroi oblasti prityazheniya G, vklyuchayushei v sebya attraktor G₀, relaksiruet k G₀. Dvizhenie, kotoromu otvechaet fazovaya traektoriya v oblasti prityazheniya, est' perehodnoi process. Ustanovivsheesya dvizhenie harakterizuetsya prinadlezhnost'yu fazovyh traektorii predel'nomu mnozhestvu, to est' attraktoru G₀.

K chemu mozhet privesti povyshenie razmernosti sistemy, naprimer do N = 3, to est' vyhod s ploskosti v trehmernoe fazovoe prostranstvo? Sovsem nedavno, do nachala 60-h godov, s uvelicheniem razmernosti fazovogo prostranstva dissipativnyh sistem svyazyvali vozmozhnost' poyavleniya (v dopolnenie k ukazannym vyshe) lish' kvaziperiodicheskih attraktorov, sootvetstvuyushih dvizheniyam na p-mernyh torah.

Vazhnym rezul'tatom issledovanii poslednih let yavilos' obnaruzhenie principial'no novyh tipov dvizhenii v dinamicheskih sistemah. Takim dvizheniyam v fazovom prostranstve razmernosti $N \ge 3$ sootvetstvuyut slozhnym obrazom ustroennye prityagivayushie mnozhestva, traektorii izobrazhayushih tochek kotoryh ne prinadlezhat ni k odnomu iz opisannyh vyshe tipov attraktorov. Fazovye traektorii predstavlyayutsya zdes' v vide beskonechnoi, nigde ne peresekayusheisya linii. Pri $t \to \infty$ traektoriya ne pokidaet zamknutoi oblasti i ne prityagivaetsya k izvestnym tipam attraktorov [2-6]. Imenno s sushestvovaniem takih traektorii svyazyvayut vozmozhnost' haoticheskogo povedeniya determinirovannyh dinamicheskih sistem s razmernost'yu fazovogo prostranstva $N \ge 3$ .

Vpervye podobnye svoistva dinamicheskoi sistemy v 1963 godu obnaruzhil E. Lorenc pri chislennom issledovanii dinamiki trehmernoi modeli teplovoi konvekcii. Spustya vosem' let v teoreticheskoi rabote D. Ryuelya i F. Takensa prityagivayushaya oblast' v fazovom prostranstve dinamicheskoi sistemy, harakterizuemaya rezhimom ustanovivshihsya neperiodicheskih kolebanii, byla nazvana strannym attraktorom. Etot termin byl srazu vosprinyat issledovatelyami i utverdilsya dlya oboznacheniya matematicheskogo obraza rezhima neregulyarnyh kolebanii determinirovannyh dinamicheskih sistem [2-6].

Attraktory v vide sostoyanii ravnovesiya, predel'nyh ciklov ili l-mernyh torov nazyvayut prostymi ili regulyarnymi, podcherkivaya tem samym, chto dvizheniya na nih otvechayut slozhivshimsya predstavleniyam ob ustoichivom po Lyapunovu determinirovannom povedenii dinamicheskoi sistemy. So strannym attraktorom svyazyvaetsya realizaciya neregulyarnogo (v smysle otsutstviya periodichnosti) kolebatel'nogo rezhima, kotoryi vo mnogom shoden s nashimi predstavleniyami o stacionarnyh sluchainyh processah.

Termin sluchainyi imeet vpolne opredelennyi smysl. Sluchainoe dvizhenie nepredskazuemo libo predskazuemo s opredelennoi veroyatnost'yu. Drugimi slovami, traektorii sluchainogo dvizheniya nel'zya mnogokratno i odnoznachno vosproizvesti ni v chislennom, ni v fizicheskom eksperimente. Primerom sluzhit klassicheskoe dvizhenie brounovskoi chasticy. V sluchae strannogo attraktora imeetsya strogaya predskazuemost' v smysle determinirovannosti zakona evolyucii. Reshenie uravnenii (kak i dlya regulyarnyh attraktorov) podchinyaetsya teoreme edinstvennosti i odnoznachno vosproizvoditsya pri fiksirovannyh nachal'nyh usloviyah. Poetomu dlya oboznacheniya slozhnyh "shumopodobnyh" avtokolebanii, matematicheskim obrazom kotoryh sluzhit strannyi attraktor, ispol'zuyutsya terminy tipa dinamicheskaya stohastichnost', determinirovannyi haos i podobnye. Vazhno otlichat' eti processy ot stohasticheskih v klassicheskom smysle, kotorye pri opisanii trebuyut ucheta fluktuacii v ishodnyh dinamicheskih uravneniyah libo neposredstvenno podchinyayutsya uravneniyam dlya plotnosti raspredeleniya veroyatnostei statisticheskoi teorii [2, 5].

Primerom sistemy s haoticheskim attraktorom yavlyayutsya uravneniya generatora s inercionnoi nelineinost'yu (generatora Anishenko-Astahova). Eta sistema yavlyaetsya obobsheniem uravnenii Van der Polya na sluchai trehmernogo prostranstva [2]:

$\dot x = mx + y -xz,$
$\dot y = -x,$ (27)
$\dot z = -gz + gI(x)x^2,$
$I(x) = \cases{1,&$x > 0$,\cr 0,&$x \le 0$.\cr}$

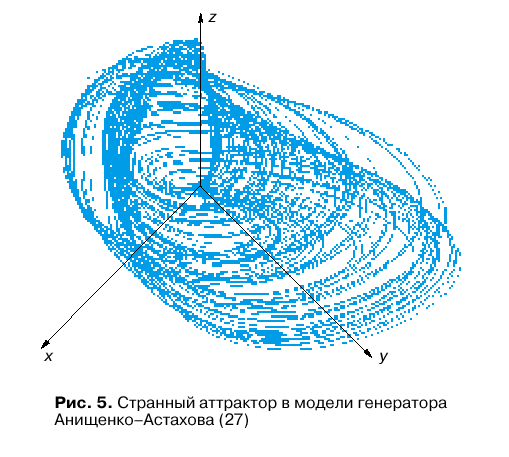
Rezul'taty chislennogo resheniya uravneniya (27) dlya znachenii parametrov m = 1,5, g = 0,2 privedeny na ris. 5, kotoryi takzhe illyustriruet haoticheskii attraktor.

Zaklyuchenie

V stat'e dano obshee opredelenie dinamicheskoi sistemy i privedeny primery dinamicheskih sistem, opisyvaemyh obyknovennymi differencial'nymi uravneniyami. Takie dinamicheskie sistemy mogut imet' chetyre tipa reshenii: sostoyanie ravnovesiya, periodicheskoe dvizhenie, kvaziperiodicheskoe dvizhenie i haoticheskoe. Etim tipam reshenii sootvetstvuyut attraktory sistemy v vide ustoichivogo ravnovesiya, predel'nogo cikla, kvaziperiodicheskogo attraktora (p-mernogo tora) i haoticheskogo (ili strannogo) attraktora. Vazhnym yavlyaetsya to, chto prosteishie tipy kvaziperiodicheskih i haoticheskih attraktorov mogut realizovyvat'sya v dinamicheskih sistemah s razmernost'yu fazovogo prostranstva ne menee treh.

Literatura

1. Anosov D.V. Dinamicheskaya sistema // Matematicheskaya enciklopediya. M.: Sov. enciklopediya, 1979.

2. Anishenko V.S. Slozhnye kolebaniya v prostyh sistemah. M.: Nauka, 1990.

3. Lihtenberg A., Liberman M. Regulyarnaya i stohasticheskaya dinamika. M.: Mir, 1984.

4. Shuster G. Determinirovannyi haos. M.: Mir, 1988.

5. Neimark Yu.I., Landa P.S. Stohasticheskie i haoticheskie kolebaniya. M.: Nauka, 1987.

6. Loskutov A.Yu., Mihailov A.S. Vvedenie v sinergetiku. M.: Nauka, 1990.

Nazad | K soderzhaniyu

Publikacii s klyuchevymi slovami: haos Publikacii so slovami: haos
Sm. takzhe: haos Vvedenie v fiziku otkrytyh sistem

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

Dinamicheskie sistemy

V. S. Anishenko

Avtokolebatel'nye sistemy

Regulyarnye i strannye attraktory dinamicheskih sistem

Zaklyuchenie

Literatura