<< 1.12. Celi yasny, nuzhny ukazaniya | Oglavlenie | 1.14. Popytka ob'yat' neob'yatnoe >>

1.13. Po bol'shomu i malomu krugam

Iskusstvennye sputniki Zemli sovershayut slozhnye dvizheniya otnositel'no nablyudatelya. Tem ne menee, v kazhdyi moment nablyudenii mozhno podobrat' bol'shoi krug, horosho predstavlyayushii peremesheniya ob'ekta po nebesnoi sfere na korotkom intervale vremeni.

Oboznachim cherez , pryamoe voshozhdenie i sklonenie polyusa bol'shogo kruga, a posredstvom , - polozhenie tochki verhnei kul'minacii. Spravedlivy prostye sootnosheniya

Na dva sosednih momenta vremeni , vychislim topocentricheskie ekvatorial'nye koordinaty ob'ekta

Vektornoe proizvedenie soderzhit koordinaty polyusa bol'shogo kruga, provedennogo cherez vektory i ,

Na lyuboi moment vremeni iz intervala vychislim topocentricheskii vektor ob'ekta v ekvatorial'noi sisteme . Ugol , otschityvaemyi po bol'shomu krugu ot tochki verhnei kul'minacii, opredelyaetsya formulami

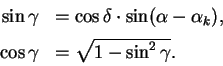
Skorost' izmeneniya ugla , velichinu , netrudno naiti metodom chislennogo differencirovaniya:

Chetyrehosnaya ustanovka pozvolyaet ispol'zovat' malyi krug nebesnoi sfery dlya nablyudenii prohozhdeniya sputnika. Pust' , - velichiny, blizkie k znacheniyam azimuta i vysoty tochki verhnei kul'minacii ob'ekta. Polyus , dlya orientacii pribora naznachim formuloi

povorot vokrug chetvertoi osi na ugol v ploskosti, prohodyashei cherez tochki polyusa i verhnei kul'minacii, privedet k tomu, chto vektor, sovpadayushii s napravleniem nablyudeniya, budet ocherchivat' na nebesnoi sfere s izmeneniem ugla polozheniya malyi krug.

Parametry malogo kruga: ustanovochnye azimut i vysota , ugol i ugol polozheniya vychislyayutsya v gorizontal'noi sisteme koordinat s pomosh'yu metoda naimen'shih kvadratov. Neobhodimo provesti ploskost', zadannuyu uravneniem

i approksimiruyushuyu polozheniya sputnika s vysotoi i azimutom na sfere edinichnogo radiusa

v razlichnye momenty vremeni za ves' interval prohozhdeniya vyshe zadannogo znacheniya vysoty .

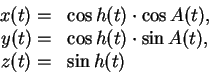
Dlya momentov vremeni vychislyaem summy proizvedeniya raznostei

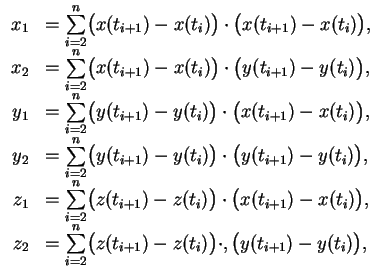
opredelyaem koefficienty , ,

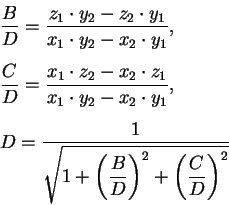
i ustanovochnye parametry

---

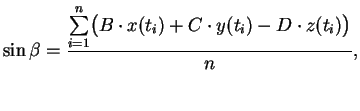
<< 1.12. Celi yasny, nuzhny ukazaniya | Oglavlenie | 1.14. Popytka ob'yat' neob'yatnoe >>

Publikacii s klyuchevymi slovami: astrometriya - lazernaya lokaciya Publikacii so slovami: astrometriya - lazernaya lokaciya
Sm. takzhe: Dostizheniya kosmicheskoi astrometrii Skonchalsya Konstantin Vladislavovich Kuimov Krasnaya Luna i zelenyi luch Konstantinu Vladislavovichu Kuimovu – 75 let Saimon N'yukom (1835 -1909) k 175-letiyu so dnya rozhdeniya. Vrashenie Zemli i prodolzhitel'nost' sutok 80 let so dnya rozhdeniya Al'berta Petrovicha Gulyaeva Vse publikacii na tu zhe temu >>