Dopolnitel'nye prostranstvennye izmereniya vhodyat v modu
Dopolnitel'nye prostranstvennye izmereniya vhodyat v modu
I.P.Ivanov
O tom, chto fiziki v poslednie gody "otkryli" v privychnom nam mire dopolnitel'nye prostranstvennye izmereniya - "v nagruzku" k vysote, dline i shirine - slyshali ne tol'ko specialisty, no i lyudi, interesuyushiesya naukoi postol'ku-poskol'ku (dlya vvedeniya v predmet chitaite zametku Trehmeren li nash mir?). Odnako sredi potoka rabot, posvyashennyh svoistvam mira s dopolnitel'nymi prostranstvennymi izmereniyami, osobnyakom stoit nedavnyaya stat'ya [N.Arkani-Hamed, A.G.Cohen, H.Georgi, Phys.Rev.Lett. 86, 4757 (2001)], predlagayushaya vzglyanut' na sut' veshei pod absolyutno novym uglom zreniya. Okazyvaetsya, v teorii polya sushestvuet vozmozhnost' dinamicheski sozdavat', generirovat' novye prostranstvennye izmereniya. Eta rabota demonstriruet, kak v obychnom chetyrehmernom prostranstve-vremeni u chastic poyavlyaetsya dopolnitel'naya stepen' svobody, kotoraya s polnym pravom mozhet byt' interpretirovana kak eshe odna prostranstvennaya koordinata.
Popytaemsya poyasnit' sut' dela. Nachnem s formal'nogo postroeniya, predlozhennogo v stat'e. Rassmotrim mir s tremya prostranstvennymi i odnim vremennym izmereniem, v kotorom sushestvuet ne privychnye nam sil'noe, slaboe i elektromagnitnoe vzaimodeistviya (gravitaciyu poka ostavim v storone), a celyi nabor razlichnyh vzaimodeistvii. A imenno, pust' u nas budet N shtuk razlichnyh po svoei prirode vzaimodeistvii, kotorye, tem ne menee, matematicheski pohozhi drug na druga (a imenno, oni opisyvaetsya odnoi i toi zhe gruppoi kalibrovochnoi simmetrii G; dlya konkretnosti avtory rassmatrivayut gruppy SU(m)). Krome togo, pust' u nas sushestvuet i veshestvo - N shtuk "adronnyh" polei, prichem kazhdoe pole chuvstvuet ne vse vozmozhnye tipy vzaimodeistvii, a tol'ko dva (nekii analog: elektrony, kotorye chuvstvuyut elektromagnitnoe i slaboe vzaimodeistvie, no ne chuvstvuyut sil'nogo).
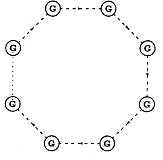 Shematicheskaya struktura mira v rassmatrivaemoi modeli: imeetsya N kalibrovochnyh polei i N polei veshestva, chuvstvitel'nyh tol'ko k pare vzaimodeistvii. |
V rezul'tate voznikaet "kol'cevaya diagramma" teorii, proillyustrirovannaya na Risunke: N uzlov diagrammy - eto vzaimodeistviya; N soedinyayushih ih linii - eto "adrony".
Okazyvaetsya, chto effektivnoe deistvie (skalyarnyi funkcional, opisyvayushii ves' mir) v takoi teorii imeet interesnuyu osobennost': krome obychnogo integrala po 4 prostranstvenno-vremennym izmereniyam imeetsya eshe i summirovanie po nomeru vzaimodeistviya ot 1 do N. Imenno na eto summirovanie avtory i obratili vnimanie. Oni ukazyvayut na to, chto imenno takoe effektivnoe deistvie voznikaet v pyatimernyh modelyah (4 prostranstvennyh izmereniya plyus vremya), v kotoryh odno prostranstvennoe izmerenie ne nepreryvno, a diskretno, chto avtomaticheski prevrashaet integral v summu.
Dalee avtory zadayutsya voprosom: naskol'ko analogiya summirovaniem po tipam vzaimodeistvii i summirovaniem po dopolnitel'noi koordinate polezna i korrektna? Razvivaya svoi idei, avtory nahodyat podtverzhdeniya tomu, chto eta dopolnitel'naya stepen' svobody v samom dele mozhet s polnym pravom nazyvat'sya eshe odnim prostranstvennym izmereniem. V chastnosti, v predele N stremitsya k beskonechnosti novaya koordinata stanovitsya nepreryvnoi. Pri etom v konstrukcii voznikaet polnaya vrashatel'naya simmetriya mezhdu vsemi chetyr'mya prostranstvennymi izmereniyami. Naprimer, svyaz' energii chasticy s impul'som imeet vid E2 = p2 + p52, gde p est' obychnyi trehmernyi impul's, a p5 - nekii kvaziimpul's, estestvennym obrazom poyavlyayushiisya v zadache (polnyi analog togo kvaziimpul'sa, kotoryi voznikaet pri kvantovo-mehanicheskom rassmotrenii N potencial'nyh yam, svernutyh v kol'co, kak pokazano na Risunke). Krome togo, esli rassmotret' potencial mezhdu dvumya chasticami kak funkciyu rasstoyaniya, to on v etoi modeli prinimaet vid 1/r2 (a ne 1/r, kak v trehmernom mire), chto takzhe govorit o real'nosti, fizichnosti novogo izmereniya.
Itak, akkuratno sformuliruem fizicheskuyu ideyu nahodki. Dopolnitel'nye prostranstvennye izmereniya ne obyazatel'no vvodit' v teoriyu rukami, kak eto delalos' do sih por. Kak pokazano v etoi stat'e, oni, v principe, mogut poluchat'sya dinamicheski. Razumeetsya, dlya etogo trebuetsya opredelennyi, dostatochno ekzoticheskii nabor fizicheskih polei i vzaimodeistvii, kotorogo, po-vidimomu, net v nashem konkretnom mire. Tem ne menee, govorit', chto eti idei k nashemu miru ne imeyut nikakogo otnosheniya, poka prezhdevremenno. V samom dele, a vdrug okazhetsya, chto odno (neskol'ko? vse?) iz nashih privychnyh prostranstvennyh izmerenii "sgenerirovany" vot takim zhe obrazom, dinamicheski, na kakom-nibud' glubokom i poka nam nedostupnom urovne?!
Kak imenno eti idei mozhno primenit' k nashemu miru, pokazhet budushee. Odnako stoit otmetit', chto stat'ya deistvitel'no privnosit sovershenno svezhuyu struyu idei v gipotezu dopolnitel'nyh prostranstvennyh izmerenii.
|
Publikacii s klyuchevymi slovami:
mnogomernoe prostranstvo - fizika elementarnyh chastic - kosmomikrofizika
Publikacii so slovami: mnogomernoe prostranstvo - fizika elementarnyh chastic - kosmomikrofizika | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |