<< Otkrytie t-kvarka | Oglavlenie | Literatura >>
Kommentarii perevodchika
Pokazhem, kak poluchayutsya formuly (2) i (3) metodami kvantovoi teorii polya.
Vezde dalee budem predpolagat', chto imeet mesto sleduyushii process:
fermion s 4-impul'som 
i antifermion s 4-impul'som 
annigiliruyut v foton ili glyuon s 4-impul'som
,
iz kotorogo rozhdaetsya para fermion-antifermion s 4-impul'sami
i 
sootvetstvenno. Fermiony v nachal'nom i konechnom
sostoyaniyah schitayutsya ul'trarelyativistskimi, to est'
. Oboznachim 
.
a) Rassmotrim reakciyu
(ris. 2 (a)).
Primem, chto 
i
. Togda, soglasno
pravilam Feinmana, poluchaem dlya matrichnogo elementa
 |
 |
 |
|
|
 |
Usrednyaya kvadrat modulya matrichnogo elementa po spinam nachal'nyh fermionov i summiruya po spinam konechnyh, nahodim
 |
|
 |
|
|
 |
gde
,
i 
-spinornye indeksy, 
-lorencovskii indeks.
V sisteme centra mass 4-impul'sy fermionov imeyut vid
 |
|||
 |
gde
, 
-ugol mezhdu napravleniyami dvizheniya
chastic 
i
. Mozhno proverit', chto dlya skalyarnyh
proizvedenii 4-vektorov spravedlivy sleduyushie formuly
Togda
 |
Ispol'zuya vyrazhenie dlya dvuhchastichnogo fazovogo ob'ema v sluchae bezmassovyh chastic
, zapishem
differencial'noe sechenie reakcii v vide
 |
Integriruya po
ot -1 do 1, poluchaem okonchatel'noe
vyrazhenie dlya polnogo secheniya
 |
kotoroe sovpadaet s formuloi (2).
b) Rassmotrim neskol'ko bolee slozhnuyu reakciyu
. Vvedem cvetovye indeksy kvarkov
i 
. Ochevidno, chto
. Matrichnyi
element reakcii imeet vid
 |
gde
- zaryad kvarka 
v edinicah 
. Uchityvaya, chto
, posle usredneniya po spinam nachal'nyh leptonov
i summirovaniyu po spinu i cvetu konechnyh kvarkov nahodim:
 |
Dlya summirovaniya po spinu i cvetu kvarkov ispol'zovalas' matrica plotnosti vida
.
Sechenie reakcii
ravno
 |
v) Teper' rassmotrim reakciyu vida
,
gde 
-virtual'nyi glyuon (ris. 2 (b)).
Pust'
, gde
- nabor iz vos'mi matric Gell-Manna razmernosti
, a
- cvetovoi indeks glyuonov.
Poyasnim, pochemu glyuony imeyut vosem' cvetovyh indeksov. Kazhdyi glyuon neset
na sebe dva cvetovyh indeksa: odin - kvarka, drugoi - antikvarka.
Naprimer, sinii-antizelenyi ili krasnyi-antikrasnyi. Kak legko
videt', vsego takih kombinacii devyat'. No kombinaciya "krasnyi-antikrasnyi
sinii-antisinii zelenyi-antizelenyi" bescvetna i ne uchastvuet
v sil'nom vzaimodeistvii. Takim obrazom, na devyat' kombinacii
kvarkovyh indeksov sushestvuet odno uslovie, chto vedet k vos'mi
nezavisimym kombinaciyam. Konechno, podobnoe rassuzhdenie ne yavlyaetsya
strogim. Matematicheski strogo vosem' glyuonnyh cvetovyh indeksov
poluchaetsya, esli ispol'zovat' teoriyu grupp (podrobnee sm., naprimer,
knigu [10]) Dlya 
-matric verny sleduyushie sootnosheniya
(sm. [10]):
i
pri 
. Primem, chto 
i chto
.
Togda dlya matrichnogo elementa processa mozhno zapisat'
 |
|
 |
|
|
 |
Usrednyaya po spinam i cvetam nachal'nyh kvarkov i summiruya po spinam i cvetam konechnyh, poluchaem vyrazhenie
 |
|
 |
|
|
 |
poskol'ku
 |
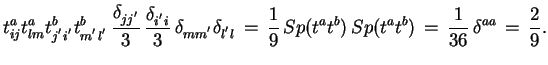Takim obrazom, dlya secheniya processa
poluchaem formulu
 |
kotoraya vosproizvodit vyrazhenie (3).
Zadacha. Pokazhite, chto sechenie processa
ravno
 |
g) Kratko ostanovimsya na reakcii
. V otlichii
ot horosho izvestnoi iz KED reakcii
, vychislenie
secheniya annigilyacii kvarkov v glyuony na poryadok bolee slozhno dazhe v
sluchae bezmassovyh kvarkov. Eto svyazano s tem, chto v KHD k dvum
annigilyacionnym diagrammam, izvestnym iz KED, dobavlyaetsya tret'ya
ot trehglyuonnoi vershiny. Bez vyvoda privedem okonchatel'nyi otvet
dlya differencial'nogo secheniya annigilyacii kvarkov v glyuony v SCM
stalkivayushihsya chastic v predele nulevyh mass kvarkov:
Rashodimost' pri
voznikla iz-za
prenebrezheniya massami stalkivayushihsya kvarkov.
Zadacha. Dannyh, privedennyh v punktah b)-g),
vpolne dostatochno, chtoby napisat' vyrazhenie dlya
. Podskazhem, chto pri
napisanii formuly (6) provodilis' usredneniya po
nachal'nym polyarizaciyam i cvetam kvarkov i summirovaniya
po konechnym polyarizaciyam i cvetam glyuonov. V sluchae reakcii
nuzhno prosummirovat' po nachal'nym polyarizaciyam
i cvetam glyuonov i usrednit' po konechnym polyarizaciyam i
cvetam kvarkov.
d) Nakonec, skazhem neskol'ko slov o vozmozhnyh kanalah raspadov
-kvarka. Absolyutno dominiruyushim yavlyaetsya kanal 
.
Shirina raspada, v prenebrezhenii massami 
-bozona i 
-kvarka,
daetsya formuloi
gde
-matrichnyi element matricy
Kabayashi-Maskava (KM-matricy). Poskol'ku KM-matrichnye elementy
kvarkovyh perehodov 
i 
ravny sootvetstvenno
i
, to raspady
po kanalam 
i 
sostavlyayut primerno 0,2% i
0,01% ot obshego chisla vseh raspadov -kvarka. Takim obrazom,
polnaya shirina raspada -kvarka prakticheski sovpadaet s parcial'noi
shirinoi raspada po kanalu .
Kak uzhe bylo otmecheno Donal'dom Perkinsom, top-kvark raspadaetsya
bystree, chem uspevaet obrazovat' svyazannoe sostoyanie. Ego vremya
zhizni sravnimo s vremenem zhizni 
-bozonov. Poetomu formal'no
mozhno utverzhdat', chto s obnaruzheniem -kvarka uvenchalis' uspehom
poiski svobodnyh kvarkov. Bolee togo, argument protivnikov kvarkovoi
modeli, zaklyuchayushiisya v tom, chto kvarki lish' udobnyi formalizm dlya
opisaniya adronov, no sami oni ne sushestvuyut, poskol'ku svobodnye kvarki
ne nablyudaemy, okazalsya oprovergnutym eksperimental'no.
Poskol'ku -kvark nastol'ko tyazhel, chto
,
to vozmozhen raspad
. Odnako on sil'no podavlen
po fazovomu ob'emu, i poetomu idet primerno v million raz rezhe,
chem raspad . Dannyi raspad interesen tem, chto ego shirina
chrezvychaino chuvstvitel'na k masse top-kvarka. Pri izmenenii 
na 10 GeV, shirina raspad
izmenyaetsya bolee chem v tri
raza. Na proton-protonnom kollaidere LHC tochnye izmereniya massy
-kvarka planiruetsya proizvesti, ispol'zuya imenno kanal
. Vozmozhny redkie raspady -kvarka
, idushie v ramkah
Standartnoi Modeli tol'ko za schet odnopetlevyh "pingvinnyh" diagramm.
No ih veroyatnost' prenebrezhimo mala, tak chto ni na odnom iz deistvuyushih
i planiruyushihsya k postroike uskoritelei oni ne mogut byt' naideny.
Do teh por, poka schitalos', chto massa neitral'nogo bozona Higgsa
nahoditsya v raione 
90 GeV, planirovalos' izuchenie kanala
raspada
. Sleduyushee iz eksperimentov na LEP-e ogranichenie
GeV zakrylo stol' interesnyi kanal.
Proton-antiprotonnyi kollaider Tevatron, kotoryi rabotaet v
nastoyashee vremya v Fermilabe, mozhet izuchat' tol'ko osnovnoi kanal
raspada -kvarka . Na stroyashemsya v CERN-e proton-protonnom
kollaidere LHC budet vozmozhno izuchat' raspady
i,
veroyatno, raspad
. Ostal'nye kanaly ne budut dostupny
eksperimental'nomu nablyudeniyu v blizhaishie desyatiletiya, esli tol'ko
verna sovremennaya teoriya vzaimodeistviya elementarnyh chastic. V
protivnom sluchae sleduet zhdat' lyubyh syurprizov. I eto osobenno
interesno!
Poluchim formulu (7) s uchetom nenulevoi massy -bozona.
Pust' 4-impul's -kvarka raven 
, a 4-impul'sy -kvarka
i -bozona i sootvetstvenno. Poskol'ku
i
, to mozhno prinyat', chto
, 
,
. Togda dlya skalyarnyh
proizvedenii
 |
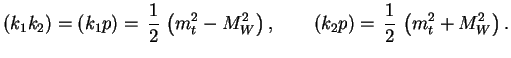Konstanta slabogo vzaimodeistviya
udovletvoryaet sleduyushemu
usloviyu
. Soglasno pravilam Feinmana
dlya matrichnogo elementa raspada
 |
Summiruya po spinam konechnyh chastic i usrednyaya po spinu nachal'noi chasticy, poluchaem
 |
|
 |
|
|
 |
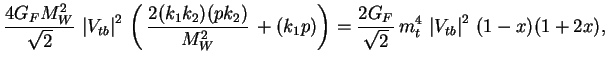gde
. Kvadrat matrichnogo elementa ne zavisit ot uglov
i modulei konechnyh impul'sov, a potomu mozhno srazu zapisat', chto
 |
Uchtya formulu dlya dvuhchastichnogo fazovago ob'ema, kogda odna iz chastic bezmassovaya
, poluchaem okonchatel'nyi
otvet
Pri
formula (8) perehodit v formulu (7).
Popravka na massu 
daet
GeV, chto dostatochno horosho soglasuetsya s gruboi ocenkoi,
privedennoi D.Perkinsom.
Zadacha. Esli v konechnom sostoyanii nahodyatsya dve chasticy s
4-impul'sami
i
,
to element dvuhchastichnogo fazovogo ob'ema opredelyaetsya kak
 |
gde
-polnyi 4-impul's sistemy, 
. Proverit', chto
verny sleduyushie vyrazheniya dlya dvuhchastichnogo fazovago ob'ema
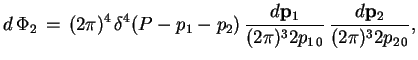v sluchae
a) bezmassovyh chastic:
;
b) odnoi massivnoi (
), odnoi bezmassovoi chastic:
, esli
;
v) dvuh massivnyh chastic s massami
i 
:
,
gde
,
esli
.
Avtor blagodarit Konstantina Tomsa za okazanie tehnicheskoi pomoshi pri podgotovke illyustracii k stat'e.
<< Otkrytie t-kvarka | Oglavlenie | Literatura >>
|
Publikacii s klyuchevymi slovami:
fizika elementarnyh chastic - kvarki
Publikacii so slovami: fizika elementarnyh chastic - kvarki | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |
