| Predydushaya | Vverh | Sleduyushaya |
2.2 Sistemy otscheta v astronomii, vidimoe dvizhenie svetil
- Prostranstvennoe raspolozhenie nebesnyh tel, priznanie ih dvizheniya, obrasheniya Luny vokrug Zemli, vozmozhnost' matematicheskogo rascheta vidimyh polozhenii planet.
- Mir ogranichen sferoi nepodvizhnyh zvezd, sohraneno ravnomernoe dvizhenie planet, sohraneny epicikly, nedostatochnaya tochnost' predskazaniya polozhenii planet.
- Neobnaruzhenie parallakticheskogo dvizheniya zvezd v silu ego malosti i pogreshnostei nablyudenii.
- Tret'ei koordinatoi v sfericheskoi sisteme koordinat yavlyaetsya modul'
radiusa-vektora - rasstoyanie do ob'ekta r. Eta koordinata opredelyaetsya
iz bolee slozhnyh nablyudenii, chem
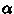 i
i 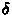 .
V katalogah ee ekvivalentom yavlyaetsya godichnyi parallaks, otsyuda
.
V katalogah ee ekvivalentom yavlyaetsya godichnyi parallaks, otsyuda 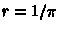 (pk). Dlya zadach sfericheskoi astronomii dostatochno znanie tol'ko dvuh
koordinat
(pk). Dlya zadach sfericheskoi astronomii dostatochno znanie tol'ko dvuh
koordinat 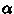 i
i 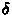 ili al'ternativnyh par koordinat:
eklipticheskih -
ili al'ternativnyh par koordinat:
eklipticheskih - 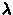 ,
, 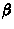 ili galakticheskih -
l, b.
ili galakticheskih -
l, b.
- Ekliptika, pervyi vertikal, kolyury ravnodenstvii i solncestoyanii.
- Na ekvatore.
- Tol'ko bol'shie krugi nebesnoi sfery proeciruyutsya v vide pryamyh linii.
- Na polyusah Zemli.
- Znacheniya A, t,
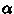 v etih sluchayah neopredelenny.
v etih sluchayah neopredelenny.
- Na severnom polyuse Zemli, na ekvatore, na yuzhnom polyuse Zemli.
- 1) A=90o, z=do
2) A=270o, z=do
- a) Na lyuboi shirote v lyuboi moment vidno polovinu nebesnoi sfery;
b) na polyusah Zemli vidna, sootvetstvenno, severnaya i yuzhnaya polusfera;
v) zha ekvatore Zemli za srok men'shii goda mozhno uvidet' vse zvezdy nebesnoi sfery.
- Na shirotah
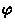 =-90o,
=-90o, 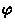 =+90o.
=+90o.
- Na ekvatore.
- Na polyusah Zemli.
- V verhnei i nizhnei kul'minaciyah.
- Na zemnom ekvatore dlya zvezd s
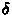 >0 A=0, a dlya zvezd s
>0 A=0, a dlya zvezd s
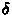 <0 A=180o.
<0 A=180o.
- V severnom polusharii dlya vseh zvezd so skloneniem
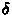 >
>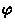 azimuty v verhnei i nizhnei kul'minaciyah odinakovy i ravny 180o.
azimuty v verhnei i nizhnei kul'minaciyah odinakovy i ravny 180o.
- Nablyudatel' nahoditsya v odnom iz polyusov Zemli ili zvezda nahoditsya v odnom iz polyusov mira.
- Bystree vsego v meridiane, medlennee vsego v pervom vertikale.
- Dlya nablyudatelya, nahodyashegosya na zemnom ekvatore i nablyudayushego zvezdu
so skloneniem
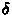 =0.
=0.
- Dlya vseh shirot - eto zvezda s
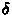 =0, na ekvatore - lyubaya
zvezda.
=0, na ekvatore - lyubaya
zvezda.
- Takoe yavlenie proishodit na ekvatore Zemli so zvezdami, nahodyashimisya na nebesnom ekvatore.
- Na ekvatore Zemli.
- V dni ravnodenstvii.
- V dni ravnodenstvii na ekvatore.
- V dni ravnodenstvii sutochnaya parallel' Solnca sovpadaet s nebesnym ekvatorom, yavlyayushimsya bol'shim krugom nebesnoi sfery. V dni solncestoyanii sutochnoi parallel'yu Solnca yavlyaetsya malyi krug, otstoyashii ot nebesnogo ekvatora na 23o.5.
- Esli prenebrech' izmeneniem skloneniya Solnca v techenie dnya, to ego voshod byl v tochke vostoka. Eto proishodit ezhegodno v dni ravnodenstvii.
- Terminator sovpadaet s zemnymi meridianami v dni ravnodenstvii.
- Kazhusheesya peremeshenie Solnca nad gorizontom bylo istolkovano kak parallakticheskoe smeshenie, a poetomu bylo ispol'zovano dlya popytki opredeleniya rasstoyaniya do svetila.
- Iskomoe mesto nahoditsya na diametral'no protivopolozhnoi tochke zemnogo
shara. Dlya Ryazani eta tochka - v yuzhnoi chasti Tihogo okeana i imeet koordinaty
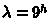 21m zapadnoi dolgoty i
21m zapadnoi dolgoty i 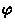 =-54o38'.
=-54o38'.
- Solnce nahoditsya v ploskosti zemnoi orbity.
- Dvazhdy v godu vo vremya dnei ravnodenstvii; odin raz v godu v dni solncestoyanii.
- Na ekvatore sumerki samye korotkie, tak kak Solnce podnimaetsya i opuskaetsya perpendikulyarno linii gorizonta. V okolopolyarnyh raionah sumerki samye dlinnye, tak kak Solnce dvizhetsya pochti parallel'no gorizontu.
- Istinnoe solnechnoe vremya.
- Mozhno, no tol'ko dlya konkretnoi daty. Dlya raznyh vidov vremeni dolzhny byt' svoi ciferblaty.
- Ritm zhizni cheloveka svyazan s Solncem, a nachalo zvezdnyh sutok popadaet na raznye chasy solnechnyh sutok.
- Sohranilis' by zvezdnyi god i sinodicheskii mesyac. Ispol'zuya ih, mozhno bylo by vvesti bolee melkie edinicy vremeni, a takzhe postroit' kalendar'.
- Samye dlinnye istinnye solnechnye sutki byvayut v dni solncestoyanii,
kogda skorost' izmeneniya pryamogo voshozhdeniya Solnca za schet ego dvizheniya
po ekliptike naibol'shaya, prichem v dekabre sutki bol'she, chem v iyune,
tak kak Zemlya v eto vremya nahoditsya v perigelii.
Samye korotkie sutki, ochevidno, v dni ravnodenstvii. V sentyabre sutki koroche, chem v marte, poskol'ku v eto vremya Zemlya blizhe k afeliyu.
- V etot period goda sklonenie Solnca ezhednevno uvelichivaetsya, i iz-za raznosti v momentah nastupleniya nachala sutok odnoi i toi zhe daty dlya zapadnyh i vostochnyh raionov Rossii dolgota dnya v Ryazani 1 maya budet bol'she, chem v bolee vostochnyh raionah.
- Osnovnaya prichina - svyaz' obshestvennoi zhizni so svetovym dnem. Neodinakovost' istinnyh solnechnyh sutok vedet k poyavleniyu srednego solnechnogo vremeni. Zavisimost' srednego solnechnogo vremeni ot dolgoty mesta obuslovila izobretenie poyasnogo vremeni. Neobhodimost' ekonomii elektroenergii privela k dekretnomu i letnemu vremeni.
- Solnechnye sutki stali by koroche zvezdnyh na chetyre minuty.
- Eto proishodit iz-za zametnogo vozrastaniya skloneniya Solnca v techenie dnya. Solnce posle poludnya opisyvaet bol'shuyu dugu na nebosvode, chem do poludnya.
- Za schet refrakcii. Solnce ran'she voshodit i pozzhe zahodit. Krome togo, v severnom polusharii Zemlya letom prohodit afelii i, sledovatel'no, dvizhetsya medlennee, chem zimoi.
- Vsledstvie refrakcii i nalichiya diska u Solnca den' okazyvaetsya dlinnee nochi.
- Eto yavlenie - sledstvie elliptichnosti zemnoi orbity. Letom Zemlya nahoditsya v afelii i ee skorost' po orbite men'she, chem skorost' v zimnie mesyacy, kogda Zemlya v perigelii.
- Bezrazlichno.
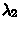 -
-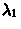 =Tm2-Tm1=S2-S1
=Tm2-Tm1=S2-S1
- Dve.
| Predydushaya | Vverh | Sleduyushaya |
|
Publikacii s klyuchevymi slovami:
zadachi - astronomicheskoe obrazovanie
Publikacii so slovami: zadachi - astronomicheskoe obrazovanie | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |
Astrometriya
-
Astronomicheskie instrumenty
-
Astronomicheskoe obrazovanie
-
Astrofizika
-
Istoriya astronomii
-
Kosmonavtika, issledovanie kosmosa
-
Lyubitel'skaya astronomiya
-
Planety i Solnechnaya sistema
-
Solnce