Rambler's Top100Astronet    
  po tekstam   po klyuchevym slovam   v glossarii   po saitam   perevod   po katalogu 		 

<< Vvedenie|Oglavlenie|Kvantovye fluktuacii na inflyacionnoi stadii >>

Haoticheskaya inflyaciya

Inflyacionnaya teoriya formulirovalas' vo mnozhestve variantov, nachinaya s modelei, osnovannyh na kvantovoi gravitacii (Starobinsky, 1980) i teorii vysokotemperaturnyh fazovyh perehodov so sverhohlazhdeniem (supercooling) i eksponencial'nym rasshireniem v sostoyanii lozhnogo vakuuma (Guth, 1981; Linde, 1982a; Albrecht and Steinhardt, 1982). Odnako, s poyavleniem scenariya haoticheskoi inflyacii (Linde, 1983b) bylo ponyato, chto osnovnye principy inflyacii ochen' prosty, i chto dlya nee vovse ne obyazatel'ny termodinamicheskoe ravnovesie, sverhohlazhdenie i rasshirenie v sostoyanii lozhnogo vakuuma.

Dlya ob'yasneniya osnovnoi idei haoticheskoi inflyacii rassmotrim prosteishuyu model' skalyarnogo polya $\phi$ s massoi $m$ i plotnost'yu potencial'noi energii $V(\phi) = {m^2\over 2} \phi^2$ (sm. ris. 1). Tak kak eta funkciya imeet minimum pri $\phi = 0$, mozhno bylo by ozhidat' oscillyacii skalyarnogo polya $\phi$ vblizi etogo minimuma. Eto deistvitel'no imeet mesto, esli vselennaya ne rasshiryaetsya. Odnako, mozhno pokazat', chto v bystro rasshiryayusheisya vselennoi skalyarnoe pole skatyvaetsya vniz ochen' medlenno, podobno shariku v vyazkoi zhidkosti, prichem effektivnaya vyazkost' okazyvaetsya proporcional'noi skorosti rasshireniya.

Evolyuciya odnorodnogo skalyarnogo polya v nashei modeli opisyvaetsya dvumya uravneniyami - uravneniem dlya polya

$$ \ddot\phi + 3H\dot\phi = -m^2\phi \ , $$

i uravneniem Einshteina

$$ H^2 +{k\over a^2} ={8\pi \over 3M_p^2}\, \left( {1\over 2}\dot \phi^2+V(\phi) \right) \ . $$

Zdes' $H = \dot a/a $ - postoyannaya Habbla dlya vselennoi s masshtabnym faktorom $a(t)$ (razmer vselennoi), $k = -1, 0, 1$ sootvetstvenno dlya otkrytoi, ploskoi i zakrytoi modelei, $M_p$ - plankovskaya massa, $M_p^{-2} = G$, gde $G$ - gravitacionnaya postoyannaya. Pervoe uravnenie pohozhe na uravnenie dvizheniya garmonicheskogo oscillyatora, gde vmesto $x(t)$ my imeem $\phi(t)$. Chlen $3H\dot\phi$ analogichen opisyvayushemu vyazkost' v uravnenii dlya garmonicheskogo oscillyatora.


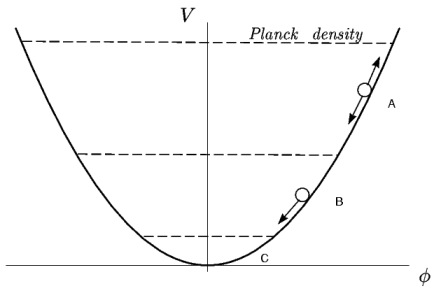
Ris. 1. Dvizhenie skalyarnogo polya v teorii s $V(\phi) = {m^2\over 2} \phi^2$. Vozmozhny neskol'ko razlichnyh rezhimov v zavisimosti ot velichiny polya $\phi$ Esli plotnost' potencial'noi energii polya prevyshaet plankovskoe znachenie $\rho \sim M_p^4 \sim 10^{94}$ g/sm$^3$, kvantovye fluktuacii prostranstva-vremeni nastol'ko sil'ny, chto ih uzhe nel'zya opisat' v obychnyh terminah. Eto sostoyanie nazyvaetsya prostranstvenno-vremennoi penoi. Na chut' men'shih energiyah (oblast' A: $m M_p^3 < V(\phi) < M_p^4$) kvantovye fluktuacii prostranstva-vremeni maly, no fluktuacii skalyarnogo polya $\phi$ mogut byt' znachitel'nymi. Skachki skalyarnogo polya, vyzvannye kvantovymi fluktuaciyami, privodyat k vechnomu samovosproizvedeniyu inflyacionnoi vselennoi (chto my obsudim nizhe). Pri eshe men'shih velichinah $V(\phi)$ (oblast' B:$m^2 M_p^2 < V(\phi) < m M_p^3$) fluktuacii skalyarnogo polya maly, ono medlenno skatyvaetsya podobno shariku v vyazkoi zhidkosti. Inflyaciya imeet mesto kak v oblasti A, tak i v oblasti B. Nakonec, vblizi minimuma $V(\phi)$ (oblast' C) skalyarnoe pole bystro oscilliruet, rozhdaya pary elementarnyh chastic, i vselennaya stanovitsya goryachei.

Esli skalyarnoe pole $\phi$ iznachal'no bylo bol'shim, postoyannaya Habbla $H$ takzhe byla velika, v sootvetstvii so vtorym uravneniem. Eto oznachaet, chto vyazkii chlen byl ochen' bol'shim, i skalyarnoe pole dvigalos' ochen' medlenno, podobno shariku v vyazkoi zhidkosti. Potomu na etoi stadii plotnost' energii skalyarnogo polya, v otlichie ot podobnoi velichiny dlya obychnoi materii, ostavalas' prakticheski postoyannoi, i rasshirenie vselennoi prodolzhalos' s gorazdo bol'shei skorost'yu, chem v staroi kosmologicheskoi teorii. Blagodarya bystromu rostu razmerov vselennoi i medlennosti dvizheniya polya $\phi$, vskore posle nachala dannoi stadii my imeem $\ddot\phi \ll 3H\dot\phi$, $H^2 \gg {k\over a^2}$, $ \dot \phi^2\ll m^2\phi^2$, tak chto mozhno uprostit' sistemu uravnenii:

$$ 3{\dot a \over a}\dot\phi = -{m^2\phi} \ , $$ $$H ={\dot a \over a} ={2 m\phi\over M_p}\, \sqrt { \pi \over 3} \ . $$

Poslednee uravnenie pokazyvaet, chto razmer vselennoi $a(t)$ na dannoi stadii rastet primerno kak $e^{Ht}$, gde $H = {2 m\phi\over M_p}\, \sqrt { \pi \over 3}\, $.

Eta stadiya eksponencial'no-bystrogo rasshireniya nazyvaetsya inflyaciei. V realistichnyh versiyah inflyacionnoi teorii ee dlitel'nost' mozhet byt' dostatochno maloi, vplot' do $10^{-35}$ sekund. Kak tol'ko pole $\phi$ stanovitsya dostatochno malym, vyazkost' takzhe umen'shaetsya, inflyaciya konchaetsya, i skalyarnoe pole nachinaet oscillirovat' vblizi minimuma $V(\phi)$. Kak lyuboe bystro oscilliruyushee klassicheskoe pole, ono teryaet energiyu za schet rozhdeniya par chastic. Eti chasticy, vzaimodeistvuya mezhdu soboi, prihodyat v teplovoe ravnovesie s nekoi temperaturoi $T$. S etogo momenta sootvetstvuyushaya chast' vselennoi mozhet byt' opisana standartnoi teoriei goryachei vselennoi.

Glavnoe otlichie inflyacionnoi teorii ot staroi kosmologii stanovitsya ochevidnym, esli poschitat' razmer tipichnoi inflyacionnoi oblasti v konce inflyacii. Dazhe esli nachal'nyi razmer inflyacionnoi vselennoi byl ochen' mal (poryadka plankovskogo dliny $l_P \sim 10^{-33}$ sm.), posle $10^{-35}$ sekundy inflyacii vselennaya dostigaet ogromnyh razmerov - $l \sim 10^{10^{12}}$ sm. Eto privodit k tomu, chto vselennaya stanovitsya prakticheski ploskoi i odnorodnoi na bol'shih masshtabah, tak kak vse neodnorodnosti rastyagivayutsya v $10^{10^{12}}$ raz.

Etot faktor yavlyaetsya model'no-zavisimym, odnako vo vseh realistichnyh modelyah vselennaya posle inflyacii okazyvaetsya na mnogo poryadkov bol'she masshtaba toi chasti vselennoi, kotoruyu my mozhem videt' ($l \sim 10^{28}$ cm). Eto srazu zhe reshaet bol'shinstvo problem klassicheskoi kosmologii (Linde, 1990a).

Rassmotrim vselennuyu, iznachal'no sostoyashuyu iz mnogih oblastei so sluchainym obrazom raspredelennym skalyarnym polem $\phi$ (ili zhe ansambl' vselennyh s razlichnymi velichinami polya). V teh chastyah, gde skalyarnoe pole slishkom malo, inflyaciya nikogda ne nachinaetsya, potomu oni ne vnosyat sushestvennogo vklada v ob'em vselennoi. Osnovnuyu zhe ee chast' zanimayut te oblasti, v kotoryh skalyarnoe pole iznachal'no bylo bol'shim. Inflyaciya takih oblastei formiruet ogromnye "ostrova" v pervichnom haose, razmer kazhdogo takogo "ostrova" sushestvenno prevyshaet razmer nablyudaemoi chasti vselennoi. Imenno poetomu ya nazyvayu etot scenarii haoticheskoi inflyaciei

Est' sushestvennoe otlichie dannogo scenariya ot staroi idei sozdaniya vsei vselennoi v nekii moment vremeni (Bol'shoi Vzryv) prakticheski odnorodnoi i nagretoi do beskonechno bol'shih temperatur. V novoi modeli bolee ne trebuyutsya usloviya iznachal'noi odnorodnosti i termodinamicheskogo ravnovesiya. Kazhdaya chast' vselennoi mozhet imet' singulyarnoe nachalo (sm. v rabote (Borde et al, 2001) obsuzhdenie sovremennogo sostoyaniya voprosa). Odnako, v kontekste haoticheskoi inflyacii eto ne oznachaet, chto vsya vselennaya kak celoe voznikla iz singulyarnosti. Razlichnye chasti vselennoi mogli voznikat' v raznye momenty vremeni, i potom razrastat'sya do razmerov, znachitel'no prevyshayushih razmer vselennoi. Nalichie nachal'noi singulyarnosti (ili singulyarnostei) ne oznachaet, chto vselennaya byla sozdana kak celoe v rezul'tate edinstvennogo Bol'shogo vzryva. Eto oznachaet, chto by bolee ne vprave govorit', chto vsya vselennaya rodilas' v nekii moment vremeni $t=0$, do kotorogo ee ne sushestvovalo. Eto spravedlivo dlya vseh variantov teorii haoticheskoi inflyacii, dazhe esli ne prinimat' vo vnimanie process samovosproizvedeniya vselennoi, obsuzhdayushiisya v razdele 4.

Vozmozhnost' togo, chto nasha odnorodnaya chast' vselennoi voznikla iz nachal'nogo haoticheskogo sostoyaniya, imeet vazhnoe znachenie dlya antropnogo principa. Do sih por my rassmatrivali prosteishuyu inflyacionnuyu model' s vsego odnim skalyarnym polem. Realistichnye modeli elementarnyh chastic, odnako, vvodyat mnozhestvo drugih skalyarnyh polei. Naprimer, v sootvetstvii so standartnoi teoriei elektroslabogo vzaimodeistviya, massy vseh elementarnyh chastic zavisyat ot velichiny higgsovskogo skalyarnogo polya $\varphi$ v nashei vselennoi. Eta velichina opredelyaetsya polozheniem minimuma effektivnogo potenciala $V(\varphi)$. V prosteishih modelyah $V(\varphi)$ imeet tol'ko odin minimum. Odnako v obshem sluchae etot potencial mozhet imet' mnozhestvo razlichnyh minimumov. Tak, v prosteishei supersimmetrichnoi teorii, ob'edinyayushei slaboe, sil'noe i elektromagnitnoe vzaimodeistviya, effektivnyi potencial imeet neskol'ko razlichnyh minimumov ravnoi glubiny po otnosheniyu k dvum skalyarnym polyam, $\Phi$ i $\varphi$. Esli eti skalyarnye polya skatyvayutsya v razlichnye minimumy v raznyh chastyah vselennoi (etot process nazyvayut spontannym narusheniem simmetrii), massy elementarnyh chastic i zakony vzaimodeistvii v nih budut razlichnymi. Kazhdaya iz etih chastei mozhet stat' eksponencial'no bol'shoi v rezul'tate inflyacii. V nekotoryh iz etih chastei ne budet raznicy mezhdu sil'nym, slabym i elektromagnitnym vzaimodeistviyami, i zhizn' nashego tipa budet nevozmozhna. Drugie zhe chasti budut pohozhi na tu, v kotoroi zhivem my (Linde, 1983c).

Eto znachit, chto dazhe esli my i naidem poslednyuyu Teoriyu Vsego (TOE, Theory of Everything), my vse ravno budem ne v sostoyanii odnoznachno predskazat' svoistva elementarnyh chastic v nashei vselennoi; vselennaya mozhet sostoyat' iz razlichnyh eksponencial'no bol'shih chastei s razlichnymi svoistvami elementarny chastic. Eto - vazhnyi shag na puti k dokazatel'stvu antropnogo principa. Sleduyushii zhe shag mozhet byt' sdelan, esli my primem vo vnimanie kvantovye fluktuacii v processe inflyacii.

<< Vvedenie|Oglavlenie|Kvantovye fluktuacii na inflyacionnoi stadii >>
Publikacii s klyuchevymi slovami: antropnyi princip - Kosmologiya - kosmologicheskaya postoyannaya - kosmomikrofizika - inflyacionnaya Vselennaya - inflyaciya - Vselennaya
Publikacii so slovami: antropnyi princip - Kosmologiya - kosmologicheskaya postoyannaya - kosmomikrofizika - inflyacionnaya Vselennaya - inflyaciya - Vselennaya
Sm. takzhe:
Vse publikacii na tu zhe temu >>

Mneniya chitatelei [16]
Ocenka: 2.8 [golosov: 125]
 
O reitinge
Versiya dlya pechati Raspechatat'

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

Astronet | Nauchnaya set' | GAISh MGU | Poisk po MGU | O proekte | Avtoram

Kommentarii, voprosy? Pishite: info@astronet.ru ili syuda

Rambler's Top100 Yandeks citirovaniya