"...Zadacha eta, kotoruyu my mozhem nazvat' "ogranichennoi problemoi v shirokom smysle", ne sovpadaet s obshei zadachei o treh telah. Opredelenie "ogranichennoi problemy" vvedeno vpervye v nebesnuyu mehaniku Puankare vvidu prakticheskoi neobhodimosti kak-to ogranichit' obshuyu zadachu o treh telah... Odna iz konechnyh mass u Puankare predpolagalas' ochen' maloi po sravneniyu s drugoi. V kopengagenstkoi zadache obe konechnye massy byli prinyaty ravnymi."
"Metod, lezhashii v osnove nashih issledovanii, est' metod chislovogo integrirovaniya differencial'nyh uravnenii dvizheniya... V processe raboty my var'irovali nachal'nye usloviya dvizheniya, chtoby ischerpat' oblast' vozmozhnyh dvizhenii vo vseh zhelatel'nyh napravleniyah."
Na risunkah vrashayushayushaya vmeste s massami m1 i m2 sistema koordinat vybrana takim obrazom, chtoby pryamaya, soedinyayushaya eti massy, sluzhila os'yu x (eto ne otnositsya k ris. 13).
"Predstavleny chertezhi, soprovozhdaemye nekotorymi poyasneniyami, predstavlyayut obshii ocherk prostyh periodicheskih i naibolee elementarnyh asimptoticheskih dvizhenii v ogranichennoi probleme i pochti ischerpyvayut raznoobrazie form dvizheniya pri izbrannom sootnoshenii mass konechnyh tel."
 | | Dve ravnyh massy dvizhutsya po krugovym orbitam vokrug obshego centra tyazhesti pod deistviem vzaimnogo prityazheniya. |
|
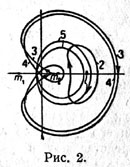 | Obratnye periodicheskie orbity vokrug L2.Orbity nachinayutsya s tochki
libracii L2, perehodyat v beskonechno maloe dvizhenie, dalee v konechnye periodicheskie orbity. Posle prohozhdeniya cherez massu m2 perehodit v orbitu s petlei. Dalee v obratnom poryadke. |
|
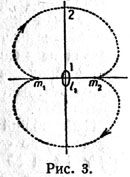 | | Obratnye periodicheskie orbity vokrug L1. Dvizhenie nachinaetsya tochkoi pokoya L1, zatem sleduet beskonechno maloe dvizhenie, zatem konechnye orbity libracionnogo tipa, zatem perehod k dvoinoi orbite vybrasyvaniya. Dalee mogut byt' razvity orbity s petlyami vokrug mass m1 i m2 |
|
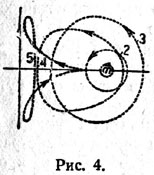 | | Pryamye periodicheskie orbity vokrug m2. Predstavlen hod razvitiya beskonechno malyh krugovyh orbit s beskonechnoi skorost'yu dvizheniya v orbity vybrasyvaniya iz m2. |
|
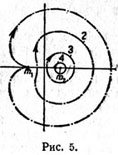 | | Obratnye periodicheskie orbity vokrug m2. Orbity razvivayutsya ot beskonechno malyh krugovyh okolo m2 s beskonechnoi skorost'yu dvizheniya v orbity vybrasyvaniya iz m1. |
|
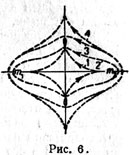 | | Pryamye periodicheskie orbity vokrug obeih mass. Orbity razvivayutsya ot orbit vybrasyvaniya k orbitam so spiralevidnymi traektoriyami, asimptoticheski priblizhayushimisya k tochkam L4 i L5. Skorost' vblizi tochek libracii delaetsya beskonechno maloi. Orbity s petlyami vokrug m1 i m2 takzhe asimptoticheski zavershayutsya okolo L4 i L5 |
|
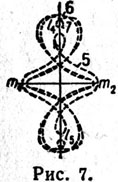 | | to zhe, chto dlya ris. 6. |
|
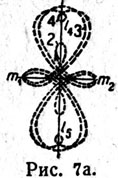 | | to zhe, chto dlya ris. 6. |
|
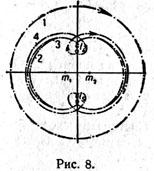 | | Vdali ot mass orbity krugovye s malymi skorostyami dvizheniya. Pri priblizhenii k massam orbity kak by splyushivayutsya. Posledovatel'no orbity prevrashayutsya v asimptoticheskoe dvizhenie okolo tochek L4 i L5. |
|
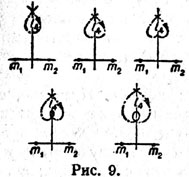 | | Pokazano razvitie form dvizheniya ot periodicheskih orbit putem obrazovaniya ryada petel' k orbitam asimptoticheskim (ris. 6, 7, 8). |
|
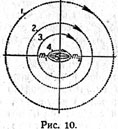 | | Obratnye periodicheskie orbity vokrug obeih mass s obratnym dvizheniem v absolyutnyh osyah: krugovaya orbita beskonechno bol'shogo radiusa s 'eskonechno medlennym dvizheniem; splyushivanie pri nepreryvnom vozrastanii skorosti dvizheniya. V konce: pryamolineinoe kolebatel'noe dvizhenie mezhdu obeimi konechnymi massami s beskonechno bol'shoi skorost'yu. |
|
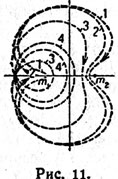 | | Obratnye, podobnye libracionnym, periodicheskie orbity, asimetrichnye otnositel'no osi ordinat. Pokazana evolyuciya form dvizheniya, vklyuchaya orbity vybrasyvaniya. |
|
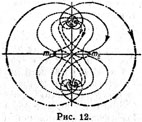 | | Pokazana sistema periodicheskih orbit, kotorye odnovremenno yavlyayutsya asimptoticheskimi po otnosheniyu k L4 i L5. |
|
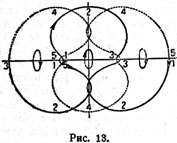 | | Dvizhenie treh tel s sootnosheniem mass 1:2:1 po orbitam, sootvetstvuyushim trem libraciyam okolo tochek L3, L1, L2. |
|
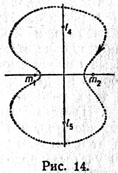 | | Obratnye, podobnye libracionnym, periodicheskie orbity. |
|
<< Nazad














