<< Pochemu imenno strunnaya teoriya ? | Oglavlenie | D-brany >>
Osnovy strunnoi teorii
My privykli dumat' ob elementarnyh chasticah (tipa elektrona) kak o tochechnyh 0-mernyh ob'ektah. Neskol'ko bolee obshim yavlyaetsya ponyatie fundamental'nyh strun kak 1-mernyh ob'ektov. Oni beskonechno tonkie, a dlina ih poryadka
. No eto prosto nichtozhno malo po
sravneniyu s dlinami, s kotorymi my obychno imeem delo, tak chto mozhno schitat', chto oni prakticheski
tochechnye. No, kak my uvidim, ih strunnaya priroda dovol'no vazhna.
Struny byvayut otkrytymi i zamknutymi. Dvigayas' v prostranstve-vremeni, oni pokryvayut poverhnost', nazyvaemuyu mirovym listom.
Eti struny imeyut opredelennye kolebatel'nye mody, kotorye opredelyayut prisushie chastice kvantovye chisla, takie, kak massa, spin, i t.d.. Osnovnaya ideya sostoit v tom, chto kazhdaya moda neset v sebe nabor kvantovyh chisel, otvechayushih opredelennomu tipu chastic. Eto i est' okonchatel'noe ob'edinenie - vse chasticy mogut byt' opisany cherez odin ob'ekt - strunu !
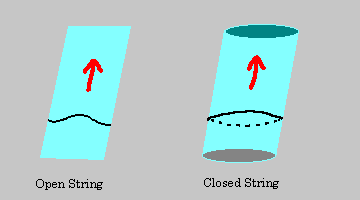
V kachestve primera rassmotrim zamknutuyu strunu, kotoraya vyglyadit tak:
Takaya struna otvechaet bezmassovomu gravitonu so spinom 2 - chastice, perenosyashei gravitacionnoe vzaimodeistvie. Kstati, eto odna iz osobennostei strunnoi teorii - ona estestvenno i neizbezhno vklyuchaet v sebya gravitaciyu kak odno iz fundamental'nyh vzaimodeistvii.
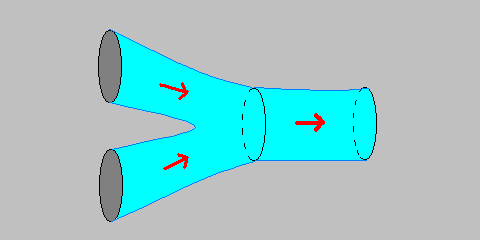
Struny vzaimodeistvuyut putem deleniya i sliyaniya. Naprimer, annigilyaciya dvuh zamknutyh strun v odnu zamknutuyu vyglyadit sleduyushim obrazom:
Otmetim, chto poverhnost' mirovogo lista - gladkaya poverhnost'. Iz etogo sleduet eshe odno "horoshee" svoistvo strunnoi teorii - v nei net ryada rashodimostei, prisushih kvantovoi teorii polya s tochechnymi chasticami. Feinmanovskaya diagramma dlya takogo zhe processa
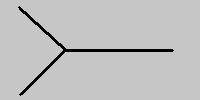
soderzhit topologicheskuyu singulyarnost' v tochke vzaimodeistviya.
Esli my "skleim" dva prosteishih strunnyh vzaimodeistviya mezhdu soboi, to poluchim process, v
kotorom dve zamknutye struny vzaimodeistvuyut cherez ob'edinenie v promezhutochnuyu zamknutuyu strunu,
kotoraya potom opyat' raspadaetsya na dve:
Etot osnovnoi vklad v process vzaimodeistviya nazyvaetsya drevesnym priblizheniem. Dlya togo,
chtoby vychislit' kvantovomehanicheskie amplitudy processov ispol'zuya teoriyu vozmushenii,
dobavlyayut vklady ot kvantovyh processov vysshih poryadkov. Teoriya vozmushenii daet horoshie rezul'taty,
tak kak vklady stanovyatsya vse men'she i men'she, kogda my ispol'zuem vse bolee vysshie poryadki. Dazhe
esli vychislit' lish' pervye neskol'ko diagramm, to mozhno poluchit' dostatochno tochnye rezul'taty. V strunnoi
teorii vysshie poryadki otvechayut bol'shemu chislu dyr (ili "ruchek") na mirovyh listah.
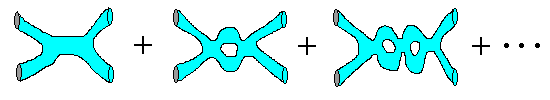
Horosho v etom podhode to, chto kazhdomu poryadku teorii vozmusheniya sootvetstvuet tol'ko odna diagramma (naprimer, v teorii polya s tochechnymi chasticami chislo diagramm rastet eksponencial'no v vysshih poryadkah). Ploho zhe to, chto tochnye raschety diagramm s bolee chem dvumya dyrami ochen' slozhny po prichine slozhnosti matematicheskogo apparata, ispol'zuemogo pri rabote s podobnymi poverhnostyami. Teoriya vozmushenii ochen' polezna pri issledovanii processov so slaboi svyaz'yu, i bol'shaya chast' otkrytii v oblasti fiziki elementarnyh chastic i strunnoi teorii svyazana imenno s nei. Odnako, vse eto eshe daleko ot zaversheniya. Otvety na samye glubokie voprosy teorii mozhno budet poluchit' lish' posle togo, kak budet zaversheno tochnoe opisanie etoi teorii.
<< Pochemu imenno strunnaya teoriya ? | Oglavlenie | D-brany >>
|
Publikacii s klyuchevymi slovami:
superstruny - supergravitaciya - kvantovaya gravitaciya - kvantovaya teoriya polya
Publikacii so slovami: superstruny - supergravitaciya - kvantovaya gravitaciya - kvantovaya teoriya polya | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |
