<< Osnovy strunnoi teorii | Oglavlenie | Superstruny >>
D-brany
U strun mogut byt' sovershenno proizvol'nye usloviya na granice. Naprimer, zamknutaya struna imeet periodichnye granichnye usloviya (struna "perehodit sama v sebya"). U otkrytyh zhe strun mogut byt' dva tipa granichnyh uslovii - usloviya Neimana i usloviya Dirihle. V pervom sluchae konec struny mozhet svobodno dvigat'sya, pravda, ne unosya pri etom impul'sa. Vo vtorom zhe sluchae konec struny mozhet dvigat'sya po nekotoromu mnogoobraziyu. Eto mnogoobrazie i nazyvaetsya D-branoi ili Dp-branoi (pri ispol'zovanii vtorogo oboznacheniya 'p' - celoe chislo, harakterizuyushee chislo prostranstvennyh izmerenii mnogoobraziya). Primer - dve struny, u kotoryh odin ili oba konca zakrepleny na 2-mernoi D-brane ili D2-brane:
D-brany mogut imet' chislo prostranstvennyh izmerenii ot -1 do chisla prostranstvennyh izmerenii nashego prostranstva-vremeni. Naprimer, v teorii superstrun 10 izmerenii - 9 prostranstvennyh i odno vremennoe. Takim obrazom, v superstrunah maksimum chto mozhet sushestvovat', eto D9-brana. Otmetim, chto v etom sluchae koncy strun fiksirovany na mnogoobrazii, pokryvayushem vse prostranstvo, poetomu oni mogut dvigat'sya vezde, tak chto na samom-to dele nalozheno uslovie Neimana ! V sluchae p=-1 vse prostranstvennye i vremennye koordinaty fiksirovany, i takaya konfiguraciya nazyvaetsya instantonom ili D-instantonom. Esli p=0, to vse prostranstvennye koordinaty fiksirovany, i konec struny mozhet sushestvovat' lish' v odnoi edinstvennoi tochke v prostranstve, tak chto D0-brany zachastuyu nazyvayut D-chasticami. Sovershenno analogichno D1-brany nazyvayut D-strunami. Kstati, samo slovo 'brana' proizoshlo ot slova 'membrana', kotorym nazyvayut 2-mernye brany, ili 2-brany.
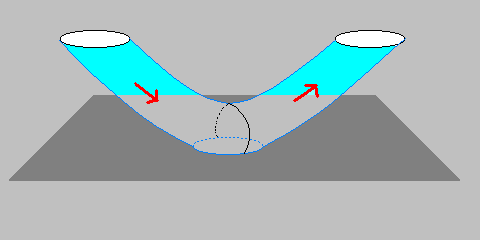
V deistvitel'nosti D-brany dinamichny, oni mogut fluktuirovat' i dvigat'sya. Naprimer, oni
vzaimodeistvuyut gravitacionno. Na diagramme nizhe mozhno videt', kak odna zamknutaya struna (v nashem
sluchae graviton) vzaimodeistvuet s D2-branoi. Osobo stoit otmetit' tot fakt, chto pri vzaimodeistvii
zamknutaya struna stanovitsya otkrytoi s oboimi koncami na D-brane.
Tak chto, strunnaya teoriya eto nechto bol'shee, chem prosto teoriya strun !
<< Osnovy strunnoi teorii | Oglavlenie | Superstruny >>
|
Publikacii s klyuchevymi slovami:
superstruny - supergravitaciya - kvantovaya gravitaciya - kvantovaya teoriya polya
Publikacii so slovami: superstruny - supergravitaciya - kvantovaya gravitaciya - kvantovaya teoriya polya | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |