<< Supersimmetrichnye struny | Oglavlenie | Dual'nost' >>
Dopolnitel'nye izmereniya
Superstruny sushestvuyut v 10-mernom prostranstve-vremeni, v to vremya kak my zhivem v 4-mernom. I esli superstruny opisyvayut nashu Vselennuyu, nam neobhodimo kak-to svyazat' mezhdu soboi dva eti prostranstva. Dlya etogo svernem 6 izmerenii do ochen' malen'kogo razmera. Esli pri etom razmer kompaktnogo izmereniya okazhetsya poryadka razmera strun (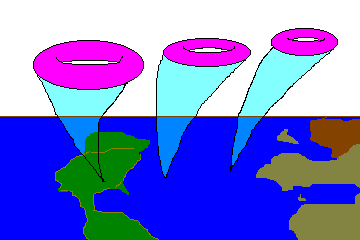
), to my
iz-za malosti etogo izmereniya poprostu ne smozhem nikak ego napryamuyu uvidet'. V konechnom itoge my poluchim nashe
(3+1)-mernoe prostranstvo, v kotorom kazhdoi tochke nashei 4-mernoi Vselennoi otvechaet krohotnoe
6-mernoe prostranstvo. Ochen' shematichno eto predstavleno na kartinke snizu:
Na samom dele eto dovol'no staraya ideya, kotoraya voshodit k rabotam Kalucy (Kaluza) i Kleina (Klein) 1920-h godov. Pri etom opisannyi vyshe mehanizm nazyvayut teoriei Kalucy-Kleina ili kompaktifikaciei. V samoi rabote Kalucy pokazano, chto esli my voz'mem teoriyu otnositel'nosti v 5-mernom prostranstve-vremeni, zatem svernem odno izmerenie v okruzhnost', to poluchim 4-mernoe prostranstvo-vremya s teoriei otnositel'nosti plyus elektromagnetizm ! A tak poluchaetsya iz-za togo, chto elektromagnetizm eto U(1) kalibrovochnaya teoriya. U(1) eto gruppa vrashenii vokrug tochki na ploskosti. Mehanizm Kalucy-Kleina daet prostuyu geometricheskuyu interpretaciyu etoi okruzhnosti - eto to samoe svernutoe pyatoe izmerenie. Hotya svernutye izmereniya i maly dlya pryamogo detektirovaniya, tem ne menee oni mogut imet' glubokii fizicheskii smysl. [Sovershenno sluchaino prosochivshis' v pressu, rabota Kalucy i Kleina vyzvala mnogo razgovorov po povodu pyatogo izmereniya.]
Kak my smozhem uznat', est' li na samom dele dopolnitel'nye izmereniya i kak my smozhem ih
"pochustvovat'", imeya uskoriteli s dostatochno vysokimi energiyami ? Iz kvantovoi mehaniki izvestno,
chto esli prostranstvo periodichno, to impul's kvantovan: 
, togda kak
esli prostranstvo neogranichenno, to spektr znachenii impul'sa nepreryven. Esli umen'shat' radius
kompaktifikacii (razmer dopolnitel'nyh izmerenii), to diapazon dozvolennyh znachenii impul'sa budet
uvelichivat'sya. Tak poluchayut bashnyu sostoyanii impul'sa - bashnyu Kalucy Kleina.
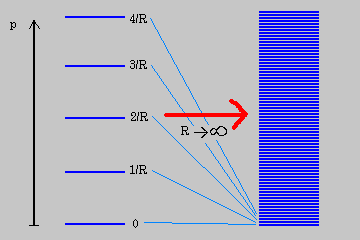
A esli radius okruzhnosti vzyat' ochen' bol'shim ("dekompaktificiruem" izmerenie), to diapazon vozmozhnyh znachenii impul'sa budet dovol'no uzkim, no budet "pochti-nepreryvnym". Takoi spektr budet pohozh na spektr mass mira bez kompaktifikacii. Naprimer, bezmassovye v bol'shem chisle izmerenii sostoyaniya v men'shem chisle izmerenii budut vyglyadet' imenno kak opisannaya vyshe bashnya sostoyanii. Togda dolzhen nablyudat'sya "nabor" chastic s massami, ravnootstoyashimi drug ot druga. Pravda, dlya togo, chtoby "uvidet'" samye massivnye chasticy, neobhodimy uskoriteli, znachitel'no luchshie teh, kotorymi my seichas raspolagaem.
U strun est' eshe odno zamechatel'noe svoistvo - oni mogut "namatyvat'sya" na kompaktificirovannoe
izmerenie, chto privodit k poyavleniyu oborotnyh mod v spektre mass. Zamknutaya struna mozhet
obernut'sya vokrug kompaktificirovannogo izmereniya celoe chislo raz. Analogichno sluchayu Kalucy-Kleina
oni dayut vklad v impul's kak 
. Sushestvennaya raznica sostoit kak raz
v drugoi svyazi s radiusom kompaktifikacii 
. V etom sluchae dlya malyh razmerov
dopolnitel'nyh izmerenii oborotnye mody stanovyatsya ochen' legkimi !
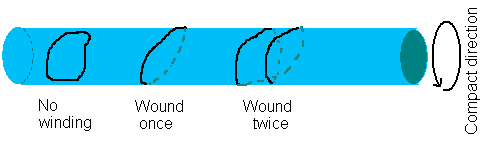
Teper' nam neobhodimo pereiti k nashemu 4-mernomu prostranstvu. Dlya etogo nam nuzhna 10-mernaya superstrunnaya teoriya na 6-mernom kompaktnom mnogoobrazii. Estestvenno, chto pri etom opisannaya vyshe kartina stanovitsya bolee slozhnoi. Proshe vsego polozhit', chto vse eti 6 izmerenii - 6 okruzhnostei, takim obrazom vse oni predstavlyayut soboi 6-mernyi tor. Bolee togo, takaya shema pozvolyaet sohranit' supersimmetriyu. Schitaetsya, chto nekotoraya supersimmetriya sushestvuet i v nashem 4-mernom prostranstve na energeticheskih masshtabah poryadka 1 TeV (imenno na etih energiyah poslednee vremya i ishut supersimmetriyu na sovremennyh uskoritelyah). Dlya togo, chtoby sohranit' minimal'nuyu supersimmetriyu, N=1 v 4-merii, kompaktificirovat' nado na special'nom 6-mernom mnogoobrazii, imenuemom mnogoobraziem Kalabi-'o (Calabi-Yau manifold).
Svoistva mnogoobrazii Kalabi-'o mogut imet' vazhnye prilozheniya k fizike nizkih energii - k chasticam, kotorye my nablyudaem, ih massam i kvantovym chislam, a takzhe k chislu pokolenii chastic. Problemoi tut yavlyaetsya to, chto, voobshe govorya, sushestvuet ogromnoe mnozhestvo mnogoobrazii Kalabi-'o, i my ne znaem, kakoe iz nih nado ispol'zovat'. V etom smysle, imeya fakticheski odnu 10-mernuyu strunnuyu teoriyu my poluchaem, chto 4-mernaya teoriya stanovitsya sovsem ne edinstvenno vozmozhnoi, po krainei mere, na nashem (eshe nepolnom) urovne ponimaniya. "Strunnye lyudi" (uchenye, rabotayushie v oblasti strunnyh teorii) vozlagayut nadezhdy na to, chto obladaya polnoi neperturbativnoi teoriei strun (teoriei, NE postroennoi na vozmusheniyah, opisannyh neskol'ko vyshe), my smozhem ob'yasnit', kak Vselennaya pereshla ot 10-mernoi fiziki, kotoraya, vozmozhno, imela mesto v techenii vysokoenergeticheskogo perioda srazu posle Bol'shogo Vzryva, k 4-mernoi, s kotoroi my imeem delo seichas. [Inymi slovami, chto my naidem edinstvennoe mnogoobrazie Kalabi-'o.] Andrei Strominger (Andrew Strominger) pokazal, chto mnogoobraziya Kalabi-'o mozhno nepreryvno svyazat' drug s drugom posredstvom konicheskih preobrazovanii (conifold transitions) i, takim obrazom, mozhno dvigat'sya mezhdu razlichnymi mnogoobraziyami Kalabi-'o, menyaya parametry teorii. No eto predpolagaet vozmozhnost' togo, chto razlichnye 4-mernye teorii, voznikayushie ot razlichnyh mnogoobrazii Kalabi-'o, yavlyayutsya razlichnymi fazami odnoi teorii.
<< Supersimmetrichnye struny | Oglavlenie | Dual'nost' >>
|
Publikacii s klyuchevymi slovami:
superstruny - supergravitaciya - kvantovaya gravitaciya - kvantovaya teoriya polya
Publikacii so slovami: superstruny - supergravitaciya - kvantovaya gravitaciya - kvantovaya teoriya polya | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |
