Klod Shennon: Matematicheskaya teoriya svyazi
<< Titul'nyi list | Oglavlenie | Chast' 1. Diskretnye sistemy bez shuma >>
Vvedenie
Nedavnee razvitie razlichnyh metodov modulyacii, takih kak PCM ili PPM, osnovannyh na uluchshenii propusknoi sposobnosti za schet umen'sheniya otnosheniya ``signal-shum'', privelo k vozrastaniyu interesa k obshei teorii svyazi. Osnovy takoi teorii zalozheny v vazhnyh stat'yah Naikvista (Nyquist, H., ``Certain Factors Affecting Telegraph Speed,'' Bell System Technical Journal, April 1924, p. 324; ``Certain Topics in Telegraph Transmission Theory,'' A.I.E.E. Trans., v. 47, April 1928, p. 617.) i Hartli(Hartley, R. V. L., ``Transmission of Information,'' Bell System Technical Journal, July 1928, p. 535.). V nastoyashei stat'e my rasshirim etu teoriyu, uchtya nekotoroe kolichestvo novyh faktorov, v chastnosti - nalichie shuma v kanale, a takzhe statisticheskuyu strukturu ishodnogo signala i prirodu konechnogo priemnika informacii.
Osnovnoi zadachei svyazi yavlyaetsya vosstanovlenie (tochnoe ili priblizhennoe) v dannoi tochke signala, otpravlennogo v drugoi. Chasto signal imeet nekoe znachenie, to est' sootnositsya ili korreliruet s zadannymi sostoyaniyami nekotoroi sistemy. Odnako eti semanticheskie aspekty svyazi ne imeyut otnosheniya k inzhenernoi zadache, vazhno lish' to, chto soobshenie vybiraetsya iz nekotorogo nabora vozmozhnyh. Sistema svyazi dolzhna odinakovo horosho rabotat' so vsemi vozmozhnymi variantami soobsheniya, a ne tol'ko s tem, kotoryi budet vybran v deistvitel'nosti - na etape razrabotki sistemy eto eshe neizvestno.
Esli nabor soderzhit konechnoe chislo soobshenii, to samo eto chislo ili lyubaya ego monotonnaya funkciya mozhet sluzhit' meroi informacii, poluchaemoi pri vybore odnogo iz nih, esli my primem vse varianty ravnoveroyatnymi. Kak bylo otmecheno Hartli, naibolee estestvenno vybrat' logarifmicheskuyu funkciyu. I hotya eto opredelenie dolzhno byt' sushestvenno obobsheno na sluchai neravnoveroyatnyh soobshenii i ih nepreryvnyh mnozhestv, my vo vseh sluchayah budem ispol'zovat' imenno logarifmicheskie mery.
Logarifmicheskaya mera udobna po sleduyushim prichinam:
- Ona udobna prakticheski. Parametry, vazhnye v inzhenernyh prilozheniyah, takie kak vremya, propusknaya sposobnost', chislo pereklyuchatelei i tak dalee obychno menyayutsya lineino pri logarifmicheskom izmenenii chisla vozmozhnyh variantov. K primeru, dobavlenie odnogo pereklyuchatelya udvaivaet chislo vozmozhnyh sostoyanii ih gruppy, uvelichivaya na edinicu ego logarifm po osnovaniyu 2. Uvelichenie v dva raza vremeni privodit k kvadratichnomu rostu chisla soobshenii, ili udvoeniyu ih logarifma, i tak dalee.
- Ona blizka k nashemu intuitivnomu predstavleniyu o takoi mere. Eto tesno svyazano s predydushim punktom, tak kak my intuitivno izmeryaem velichiny, lineino sravnivaya ih so standartami. Tak, nam kazhetsya, chto na dvuh perfokartah mozhno razmestit' v dva raza bol'she informacii, a po dvum odinakovym kanalam - peredat' ee v dva raza bol'she.
- Ona udobna matematicheski. Mnogie predel'nye perehody prosty v logarifmah, v to vremya kak v terminah chisla variantov oni dostatochno netrivial'ny.
Vybor osnovaniya logarifma sootvetstvuet vyboru edinicy izmereniya informacii.
Esli vzyat' osnovanie 2, to poluchennye edinicy mozhno nazvat' ``dvoichnymi ciframi'',
ili bitami (binary digits -> bits, slovo predlozheno Dzh.V.Taki, J.W.Tukey)
Ustroistvo s dvumya ustoichivymi sostoyaniyami, takoe kak pereklyuchatel' ili
trigger, sposobno hranit' odin bit informacii, ![]() takih ustroistv
-
takih ustroistv
- ![]() bit, tak kak polnoe chislo sostoyanii
bit, tak kak polnoe chislo sostoyanii ![]() i
i
![]() . Pri ispol'zovanii zhe osnovaniya 10 edinicy mozhno
nazvat' ``desyatichnymi ciframi''. Tak kak ,
desyatichnaya cifra primerno sootvetstvuet
. Pri ispol'zovanii zhe osnovaniya 10 edinicy mozhno
nazvat' ``desyatichnymi ciframi''. Tak kak ,
desyatichnaya cifra primerno sootvetstvuet ![]() bit. Cifrovoe
koleso arifmometra imeet 10 ustoichivyh sostoyanii, i potomu mozhet hranit' odnu
desyatichnuyu cifru informacii. V analiticheskih raschetah, pri provedenii differencirovaniya
i integrirovaniya, byvaet polezno ispol'zovat' natural'nyi logarifm, to est'
osnovanie
bit. Cifrovoe
koleso arifmometra imeet 10 ustoichivyh sostoyanii, i potomu mozhet hranit' odnu
desyatichnuyu cifru informacii. V analiticheskih raschetah, pri provedenii differencirovaniya
i integrirovaniya, byvaet polezno ispol'zovat' natural'nyi logarifm, to est'
osnovanie ![]() . Sootvetstvuyushie edinicy informacii mozhno nazvat'
natural'nymi. Perehod ot osnovaniya
. Sootvetstvuyushie edinicy informacii mozhno nazvat'
natural'nymi. Perehod ot osnovaniya ![]() k
k ![]() svoditsya
k umnozheniyu na
svoditsya
k umnozheniyu na ![]() .
.
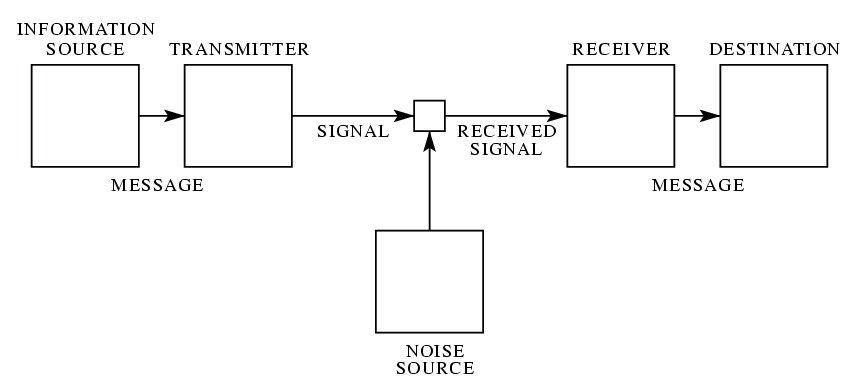
Ris. 1. Shematicheskoe izobrazhenie obshei sistemy svyazi.
Pod sistemoi svyazi my budem ponimat' sistemu tipa izobrazhennoi na ris.1. Takaya sistema sostoit iz 5 chastei:
-
Istochnika informacii, ispuskayushego soobshenie ili seriyu soobshenii dlya
svyazi s priemnoi stanciei. Soobsheniya mogut byt' razlichnyh tipov: (a)
posledovatel'nost'yu bukv, kak v telegrafnoi sisteme, (b) nekotoroi
funkciei vremeni
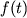 , kak v sisteme telefonnoi svyazi, (v)
funkciei vremeni i drugih peremennyh, kak v televizionnyh sistemah - takoe
soobshenie mozhno rassmatrivat' kak funkciyu
, kak v sisteme telefonnoi svyazi, (v)
funkciei vremeni i drugih peremennyh, kak v televizionnyh sistemah - takoe
soobshenie mozhno rassmatrivat' kak funkciyu 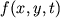 dvuh prostranstvennyh
koordinat i vremeni, predstavlyayushuyu intensivnost' izlucheniya v tochke
dvuh prostranstvennyh
koordinat i vremeni, predstavlyayushuyu intensivnost' izlucheniya v tochke 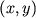 v moment vremeni
v moment vremeni 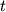 na fotokatode; (g) dvumya ili bolee
funkciyami vremeni, k primeru
na fotokatode; (g) dvumya ili bolee
funkciyami vremeni, k primeru 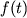 ,
, 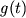 ,
, 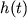 ,
kak v sluchae peredachi ``trehmernogo zvuka'' ili prosto neskol'kih signalov odnovremenno;
(d) neskol'kimi funkciyami neskol'kih peremennyh - pri peredache cvetnogo televizionnogo
signala my imeem delo s tremya funkciyami
,
kak v sluchae peredachi ``trehmernogo zvuka'' ili prosto neskol'kih signalov odnovremenno;
(d) neskol'kimi funkciyami neskol'kih peremennyh - pri peredache cvetnogo televizionnogo
signala my imeem delo s tremya funkciyami 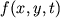 ,
,
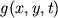 ,
, 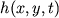 , opredelennymi na trehmernom
mnozhestve (my mozhem rassmatrivat' tri etih funkcii takzhe kak komponenty
trehmernogo vektornogo polya v prostranstve); krome togo, razlichnye vidy
signalov mogut voznikat' pri peredache televizionnogo izobrazheniya sovmestno so zvukom
kanalom.
, opredelennymi na trehmernom
mnozhestve (my mozhem rassmatrivat' tri etih funkcii takzhe kak komponenty
trehmernogo vektornogo polya v prostranstve); krome togo, razlichnye vidy
signalov mogut voznikat' pri peredache televizionnogo izobrazheniya sovmestno so zvukom
kanalom.
- Peredatchika, preobrazuyushego nekim obrazom signal i delayushego ego prigodnym dlya peredachi po linii svyazi. V telefonii eto svoditsya glavnym obrazom k preobrazovaniyu davleniya zvuka v proporcional'nyi elektricheskii signal. V sluchae telegrafa process kodirovaniya signala preobrazuet ego v posledovatel'nost' tochek, tire i probelov v linii svyazi. V mnogokanal'noi PCM-sisteme razlichnye funkcii razlichnyh golosov dolzhny byt' diskretizovany, szhaty, zakodirovany i, nakonec, svedeny nadlezhashim obrazom v odin signal. Vokodery (ustroistva cifrovogo kodirovaniya rechi), televidenie i chastotnaya modulyaciya - drugie primery slozhnyh preobrazovanii, kotorym mozhet byt' podvergnuto soobshenie pri formirovanii signala.
- Kanala, predstavlyayushego soboi sredu, ispol'zuemuyu dlya peredachi signala ot peredatchika k priemniku. On mozhet byt' paroi provodov, koaksial'nym kabelem, radiovolnami opredelennoi chastoty, luchom sveta i t.d.
- Priemnika, vypolnyayushego zadachi, protivopolozhnye vypolnyaemym peredatchikom, a imenno - vosstanovleniya soobsheniya iz signala.
- Punkta naznacheniya - cheloveka (ili ustroistvo), dlya kotorogo soobshenie prednaznacheno.
My hoteli by rassmotret' nekotorye obshie zadachi, imeyushie otnoshenie k sistemam svyazi. Dlya etogo neobhodimo snachala predstavit' razlichnye vysheupomyanutye elementy matematicheskimi velichinami, otvlekayas' ot ih fizicheskoi sushnosti. Sistemy svyazi mozhno grubo razdelit' na tri kategorii: diskretnye, nepreryvnye i smeshannye. Pod diskretnoi sistemoi budem ponimat' takuyu, v kotoroi i soobshenie, i signal yavlyayutsya posledovatel'nostyami diskretnyh simvolov. Tipichnym primerom takoi sistemy yavlyaetsya telegrafiya, v kotoroi i soobshenie, i signal yavlyayutsya posledovatel'nostyami tochek, tire i promezhutkov mezhdu nimi. Nepreryvnaya sistema - takaya, v kotoroi i soobshenie, i signal rassmatrivayutsya kak nepreryvnye funkcii, naprimer, v radio ili televidenii. V smeshannoi sisteme, sootvetstvenno, figuriruyut kak nepreryvnye, tak i diskretnye velichiny, kak, naprimer, v PCM-sisteme peredachi rechi.
Rassmotrim vnachale diskretnyi sluchai. On imeet prilozheniya ne tol'ko v teorii svyazi, no takzhe i v teorii vychislitel'nyh mashin i tak dalee. Vdobavok diskretnye sistemy yavlyayutsya osnovoi dlya rassmotreniya nepreryvnyh i smeshannyh, kotorye razbirayutsya vo vtoroi polovine stat'i.
<< Titul'nyi list | Oglavlenie | Chast' 1. Diskretnye sistemy bez shuma >>
|
Publikacii s klyuchevymi slovami:
matematika - informaciya - Shennon
Publikacii so slovami: matematika - informaciya - Shennon | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |