Klod Shennon: Matematicheskaya teoriya svyazi
<< Vvedenie | Oglavlenie | Chast' 2. Diskretnyi zashumlennyi kanal >>
Chast' 1. Diskretnye sistemy bez shuma
Diskretnyi kanal bez shuma
Teletaip i telegraf - dva prostyh primera diskretnyh kanalov dlya peredachi informacii.
V obshem sluchae budem nazyvat' diskretnym kanalom sistemu, posredstvom kotoroi
posledovatel'nost' vyborov iz nabora elementarnyh simvolov ![]() mozhet byt' peredana iz odnoi tochki v druguyu. Kazhdyi iz etih simvolov
mozhet byt' peredana iz odnoi tochki v druguyu. Kazhdyi iz etih simvolov ![]() predpolagaetsya imeyushim nekotoruyu protyazhennost' vo vremeni
predpolagaetsya imeyushim nekotoruyu protyazhennost' vo vremeni ![]() (ne obyazatel'no odinakovuyu dlya razlichnyh simvolov). Ne trebuetsya vozmozhnost'
peredachi proizvol'noi posledovatel'nosti simvolov, vpolne dopustim variant
s ogranichennym naborom razreshennyh posledovatel'nostei. Eto - vozmozhnye signaly
v kanale. K primeru, v telegrafii takimi simvolami yavlyayutsya: (1)
tochka, sootvetstvuyushaya zamykaniyu linii na edinichnoe vremya i razmykaniyu toi zhe
dlitel'nosti, (2) tire, sootvetstvuyushee zamykaniyu linii na tri edinicy vremeni
i razmykaniyu na odnu, (3) promezhutok mezhdu bukvami, sootvetstvuyushii,
k primeru, razmykaniyu linii na tri edinicy vremeni, i (4) promezhutok
mezhdu slovami, sootvetstvuyushii razmykaniyu linii na shest' edinic vremeni.
My mozhem ogranichit' vozmozhnye posledovatel'nosti simvolov, zapretiv k primeru
posledovatel'nye promezhutki (tak kak dva sleduyushih drug za drugom bukvennyh
promezhutka identichny promezhutku mezhdu slovami). Vopros, kotoryi my seichas
rassmotrim, sostoit v tom, kak opredelit' propusknuyu sposobnost' takogo kanala.
(ne obyazatel'no odinakovuyu dlya razlichnyh simvolov). Ne trebuetsya vozmozhnost'
peredachi proizvol'noi posledovatel'nosti simvolov, vpolne dopustim variant
s ogranichennym naborom razreshennyh posledovatel'nostei. Eto - vozmozhnye signaly
v kanale. K primeru, v telegrafii takimi simvolami yavlyayutsya: (1)
tochka, sootvetstvuyushaya zamykaniyu linii na edinichnoe vremya i razmykaniyu toi zhe
dlitel'nosti, (2) tire, sootvetstvuyushee zamykaniyu linii na tri edinicy vremeni
i razmykaniyu na odnu, (3) promezhutok mezhdu bukvami, sootvetstvuyushii,
k primeru, razmykaniyu linii na tri edinicy vremeni, i (4) promezhutok
mezhdu slovami, sootvetstvuyushii razmykaniyu linii na shest' edinic vremeni.
My mozhem ogranichit' vozmozhnye posledovatel'nosti simvolov, zapretiv k primeru
posledovatel'nye promezhutki (tak kak dva sleduyushih drug za drugom bukvennyh
promezhutka identichny promezhutku mezhdu slovami). Vopros, kotoryi my seichas
rassmotrim, sostoit v tom, kak opredelit' propusknuyu sposobnost' takogo kanala.
V sluchae teletaipa, v kotorom vse simvoly imeyut odnu i tu zhe dlitel'nost' i
razreshena lyubaya kombinaciya 32-h simvolov, otvet prost. Kazhdyi simvol predstavlyaet soboi
pyat' bit informacii. Esli sistema svyazi peredaet ![]() simvolov v sekundu,
estestvenno skazat', chto propusknaya sposobnost' kanala
simvolov v sekundu,
estestvenno skazat', chto propusknaya sposobnost' kanala ![]() bit
v sekundu. Eto ne znachit, chto teletaip vsegda peredaet informaciyu s
takoi skorost'yu - eto lish' maksimal'no vozmozhnyi temp, i budet ili net on dostigat'sya -
zavisit ot istochnika informacii, podavaemoi v kanal (sm. dalee)
bit
v sekundu. Eto ne znachit, chto teletaip vsegda peredaet informaciyu s
takoi skorost'yu - eto lish' maksimal'no vozmozhnyi temp, i budet ili net on dostigat'sya -
zavisit ot istochnika informacii, podavaemoi v kanal (sm. dalee)
Dlya bolee obshego sluchaya razlichnoi dliny simvolov i ogranichenii na razreshennye posledovatel'nosti dadim sleduyushee opredelenie:
Opredelenie: Propusknaya sposobnost' ![]() kanala daetsya
vyrazheniem
kanala daetsya
vyrazheniem
gde ![]() - chislo vozmozhnyh signalov dlitel'nosti
- chislo vozmozhnyh signalov dlitel'nosti ![]() .
.
Legko videt', chto v sluchae teletaipa etot rezul'tat svoditsya v predydushemu.
Mozhno pokazat', chto etot predel v bol'shinstve interesuyushih nas sluchaev sushestvuet
i yavlyaetsya konechnym. Predpolozhim, chto razresheny vse posledovatel'nosti simvolov
![]() dlitel'nost'yu
dlitel'nost'yu ![]() sootvetstvenno.
Kakova propusknaya sposobnost' kanala? Esli
sootvetstvenno.
Kakova propusknaya sposobnost' kanala? Esli ![]() - chislo posledovatel'nostei
dlitel'nosti
- chislo posledovatel'nostei
dlitel'nosti ![]() ,
,
Polnoe chislo ravno summe chisel posledovatel'nostei, okanchivayushihsya na
![]() , to est'
, to est' ![]() ,
sootvetstvenno. Soglasno shiroko izvestnomu rezul'tatu diskretnogo analiza,
,
sootvetstvenno. Soglasno shiroko izvestnomu rezul'tatu diskretnogo analiza,
![]() pri bol'shih
pri bol'shih ![]() asimptoticheski stremitsya k
asimptoticheski stremitsya k
![]() , gde
, gde ![]() - naibol'shii deistvitel'nyi koren'
harakteristicheskogo uravneniya:
- naibol'shii deistvitel'nyi koren'
harakteristicheskogo uravneniya:
i sledovatel'no
Pri nalichii ogranichenii na razreshennye posledovatel'nosti simvolov my zachastuyu
takzhe mozhem poluchit' raznostnoe uravnenie takogo tipa i naiti ![]() iz
harakteristicheskogo uravneniya. V vysheupomyanutom sluchae telegrafnoi sistemy
iz
harakteristicheskogo uravneniya. V vysheupomyanutom sluchae telegrafnoi sistemy
chto poluchaetsya pri uchete poslednego i predposlednego simvolov.
Sledovatel'no, ![]() ravno
ravno ![]() , gde
, gde
![]() - polozhitel'nyi koren' uravneniya
- polozhitel'nyi koren' uravneniya
![]() .
Reshaya ego, nahodim
.
Reshaya ego, nahodim ![]() .
.
Dostatochno obshim vidom ogranichenii na vozmozhnye posledovatel'nosti simvolov
mozhet byt' sleduyushii. Rassmotrim mnozhestvo vozmozhnyh sostoyanii ![]() .
V kazhdom sostoyanii mogut peredavat'sya lish' nekotorye simvoly iz nabora
.
V kazhdom sostoyanii mogut peredavat'sya lish' nekotorye simvoly iz nabora
![]() (razlichnye podmnozhestva v razlichnyh sostoyaniyah).
Pri peredache odnogo iz etih simvolov sostoyanie izmenyaetsya v zavisimosti kak
ot predydushego sostoyaniya, tak i ot peredannogo simvola. Prostym primerom takoi
sistemy yavlyaetsya telegraf, kotoryi mozhet nahodit'sya v odnom iz dvuh sostoyanii
v zavisimosti ot togo, byl li poslednim peredannym simvolom 'probel'. Esli
da, to mozhet byt' poslany tol'ko tochka ili tire, i sostoyanie izmenitsya na
protivopolozhnoe. Esli zhe net, mozhet byt' poslan proizvol'nyi simvol, i sostoyanie
izmenitsya, esli poslannyi simvol - 'probel'. Eta situaciya illyustriruetsya
lineinym grafom, izobrazhennym na ris.2.
(razlichnye podmnozhestva v razlichnyh sostoyaniyah).
Pri peredache odnogo iz etih simvolov sostoyanie izmenyaetsya v zavisimosti kak
ot predydushego sostoyaniya, tak i ot peredannogo simvola. Prostym primerom takoi
sistemy yavlyaetsya telegraf, kotoryi mozhet nahodit'sya v odnom iz dvuh sostoyanii
v zavisimosti ot togo, byl li poslednim peredannym simvolom 'probel'. Esli
da, to mozhet byt' poslany tol'ko tochka ili tire, i sostoyanie izmenitsya na
protivopolozhnoe. Esli zhe net, mozhet byt' poslan proizvol'nyi simvol, i sostoyanie
izmenitsya, esli poslannyi simvol - 'probel'. Eta situaciya illyustriruetsya
lineinym grafom, izobrazhennym na ris.2.

Ris. 2. Graficheskoe predstavlenie ogranichenii na posledovatel'nosti telegrafnyh simvolov.
Teorema 1. Pust' ![]() - dlitel'nost' simvola
- dlitel'nost' simvola
![]() , razreshennogo v sostoyanii
, razreshennogo v sostoyanii ![]() i privodyashego k perehodu
sistemy v sostoyanie
i privodyashego k perehodu
sistemy v sostoyanie ![]() . Togda propusknaya sposobnost' kanala
. Togda propusknaya sposobnost' kanala ![]() ravnyaetsya
ravnyaetsya ![]() , gde
, gde ![]() - naibol'shii deistvitel'nyi
koren' deterministicheskogo uravneniya
- naibol'shii deistvitel'nyi
koren' deterministicheskogo uravneniya
gde ![]() pri
pri ![]() i ravno nulyu inache.
i ravno nulyu inache.
K primeru, v sluchae telegrafa (ris. 2) determinant raven
chto pri raskrytii daet vysheprivedennoe uravnenie dlya dannogo sluchaya.
Diskretnyi istochnik informacii
My videli, chto pri dostatochno obshih usloviyah logarifm chisla vozmozhnyh signalov v diskretnom kanale lineino rastet so vremenem. Propusknaya sposobnost' kanala mozhet byt' oharakterizovana tempom etogo rosta, chislom bit v sekundu, neobhodimyh dlya peredachi dannogo konkretnogo signala.
Rassmotrim teper' istochnik informacii. Kak on mozhet byt' opisan matematicheski, i skol'ko bit informacii v sekundu on proizvodit? Vazhnym tut yavlyaetsya znanie o statistike etogo istochnika, chto pozvolyaet ponizit' trebuemuyu propusknuyu sposobnost' kanala vyborom sootvetstvuyushei kodirovki - predstavleniya informacii. V telegrafii, k primeru, peredavaemye soobsheniya sostoyat iz posledovatel'nostei bukv. Eti posledovatel'nosti, odnako, ne yavlyayutsya sovershenno sluchainymi. V obshem sluyaae oni obrazuyut predlozheniya i imeyut statisticheskuyu prirodu, skazhem, angliiskogo yazyka. Bukva E vstrechaetsya chashe Q, posledovatel'nost' TH - chashe, chem XP. Nalichie takoi struktury pozvolyaet poluchit' vyigrysh vo vremeni peredachi soobsheniya (ili propusknoi sposobnosti kanala), sootvetstvuyushim obrazom ego kodiruya. Imenno takoi podhod ispol'zuetsya v telegrafii, gde samyi korotkii simvol - tochka - ispll'zuetsya dlya naibolee chasto ispol'zuemoi angliiskoi bukvy E, v to vremya kak samye redkie - Q, X, Z - predstavlyayutsya bolee dlinnymi posledovatel'nostyami tochek i tire. Eshe bol'shii vyigrysh vo vremeni peredachi dostigaetsya v nekotoryh kommercheskih sistemah kodirovaniya, v kotoryh naibolee rasprostranennye frazy i vyrazheniya zamenyayutsya chetyreh- ili pyatibukvennymi kombinaciyami. Ispol'zuyushiesya v nastoyashee vremya standartizovannye pozdravitel'nye i privetstvennye telegrammy takzhe pozvolyayut kodirovat' cerye predlozheniya dostatochno korotkimi posledovatel'nostyami chisel. v nastoyashee vremya
Mozhno schitat', chto diskretnyi istochnik formiruet soobshenie simvol za simvolom, vybiraya ih v sootvetstvii s nekotoroi veroyatnost'yu, zavisyashei kak ot nomera simvola, tak i ot predydushih vyborov. Fizicheskaya sistema, ili zhe matematicheskaya model' sistemy, generiruyushei takuyu posledovatel'nost' simvolov v sootvetstvii s naborom veroyatnostei, predstavlyaet soboi stohasticheskii process (Sm., naprimer, S. Chandrasekhar, ``Stochastic Problems in Physics and Astronomy,'' Reviews of Modern Physics, v. 15, No. 1, January 1943, p. 1.). Takim obrazom, my mozhem rassmatrivat' diskretnyi istochnik kak stohasticheskii process, i naoborot, lyuboi stohasticheskii process, generiruyushii diskretnuyu posledovatel'nost' simvolov iz ogranichennogo mnozhestva mozhno schitat' diskretnym istochnikom. Eto vklyuchaet v sebya:
- Estestvennye yazyki, takie, kak angliiskii, nemeckii i kitaiskii.
- Nepreryvnye istochniki informacii, kotoraya mozhet byt' diskretizovana v rezul'tate nekotoroi operacii, naprimer, ocifrovannaya rech' v PCM-peredatchike, ili diskretnyi televizionnyi signal.
-
Chisto matematicheskie sluchai, kogda my abstraktno opredelyaem nekotoryi
stohasticheskii process, generiruyushii posledovatel'nost' simvolov. Dadim
neskol'ko primerov etogo tipa.
- (A)
Pust' u nas est' pyat' bukv A, B, C, D, E,
kotorye vybirayutsya s ravnoi veroyatnost'yu 0.2, prichem kazhdyi iz etih vyborov
ne zavisit ot predydushih. Togda tipichnoi posledovatel'nost'yu simvolov budet,
k primeru,
B D C B C E C C C A D C B D D A A E C E E A A B B D A E E C A C E E B A E E C B C E A D.
Dannaya posledovatel'nost' byla postroena s ispol'zovaniem tablicy sluchainyh chisel(Kendall and Smith, Tables of Random Sampling Numbers, Cambridge, 1939.). - (B)
Ispol'zuya te zhe samye pyat' bukv, no s veroyatnostyami 0.4, 0.1, 0.2, 0.2, 0.1
sootvetstvenno, poluchaem sleduyushee tipichnoe soobshenie:
A A A C D C B D C E A A D A D A C E D A E A D C A B E D A D D C E C A A A A A D.
-
(C) Bolee slozhnaya struktura mozhet byt' poluchena pri otkaze ot vzaimnoi nezavisimosti otdel'nyh procedur vybora - to est' togda, kogda kazhdyi posleduyushii simvol zavisit ot predydushih. V prosteishem sluchae kazhdyi simvol zavisit lish' ot predydushego i ne zavisit ot bolee rannih. Statisticheskaya struktura togda mozhet byt' predstavlena naborom veroyatnostei perehoda
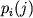 , to est' veroyatnostei togo, chto za simvolom
, to est' veroyatnostei togo, chto za simvolom 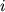 budet sledovat' simvol
budet sledovat' simvol 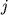 . Vtorym ravnocennym metodom opisaniya
takoi struktury yavlyayutsya veroyatnosti 'digramm' (dvuhbukvennyh kombinacii
. Vtorym ravnocennym metodom opisaniya
takoi struktury yavlyayutsya veroyatnosti 'digramm' (dvuhbukvennyh kombinacii 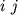 )
)
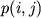 . Chastoty vstrechaemosti bukv
. Chastoty vstrechaemosti bukv 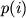 (veroyatnost'
bukvy
(veroyatnost'
bukvy 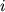 ), veroyatnosti perehoda
), veroyatnosti perehoda 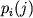 i veroyatnosti
digramm
i veroyatnosti
digramm 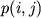 svyazany sleduyushimi vyrazheniyami:
svyazany sleduyushimi vyrazheniyami:
Dlya primera voz'mem tri bukvy A, B,C s tablicami veroyatnostei:
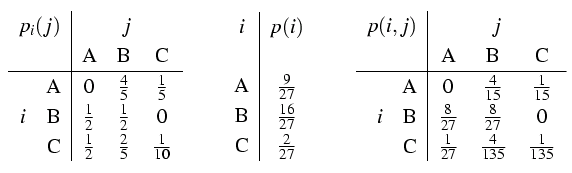
A B B A B A B A B A B A B A B B B A B B B B B A B A B A B A B A B B B A C A C A B B A B B B B A B B A B A C B B B A B A.
Sleduyushim po slozhnosti budet uchet chastot vstrechaemosti trigramm, to est' situaciya, pri kotoroi vybor tekushego simvola zavisit lish' ot dvuh predshestvuyushih. V dannoi situacii trebuetsya znanie veroyatnostei trigramm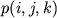 ,
ili, chto to zhe samoe, veroyatnostei perehodov
,
ili, chto to zhe samoe, veroyatnostei perehodov 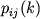 . Pri
dal'neishem obobshenii mozhno poluchit' i signaly s bolee slozhnoi strukturoi.
Tak, v obshem sluchae trebuetsya znanie nabora veroyatnostei $n$-gramm
. Pri
dal'neishem obobshenii mozhno poluchit' i signaly s bolee slozhnoi strukturoi.
Tak, v obshem sluchae trebuetsya znanie nabora veroyatnostei $n$-gramm 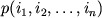 ili zhe veroyatnostei perehoda
ili zhe veroyatnostei perehoda 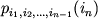 .
.
- (D)
Mozhno takzhe opredelit' stohasticheskii process, generiruyushii tekst, yavlyayushiisya
posledovatel'nost'yu ``slov''. Pust' est' pyat' bukv A, B, C, D,
E i 16 ``slov'' yazyka s sootvetstvuyushimi veroyatnostyami:
Pust' eti slova vybirayutsya nezavisimo i razdelyayutsya probelom. Togda tipichnym soobsheniem budet:.10 A .16 BEBE .11 CABED .04 DEB .04 ADEB .04 BED .05 CEED .15 DEED .05 ADEE .02 BEED .08 DAB .01 EAB .01 BADD .05 CA .04 DAD .05 EE DAB EE A BEBE DEED DEB ADEE ADEE EE DEB BEBE BEBE BEBE ADEE BED DEED DEED CEED ADEE A DEED DEED BEBE CABED BEBE BED DAB DEED ADEB.
Esli vse slova imeyut ogranichennuyu dlinu, dannyi process svoditsya k odnomu iz vysheopisannyh, odnako opisanie ego budet proshe v terminah struktury i veroyatnostei slov. Mozhno poiti dalee i vvesti veroyatnosti perehoda mezhdu slovami, i tak dalee.
- (A)
Pust' u nas est' pyat' bukv A, B, C, D, E,
kotorye vybirayutsya s ravnoi veroyatnost'yu 0.2, prichem kazhdyi iz etih vyborov
ne zavisit ot predydushih. Togda tipichnoi posledovatel'nost'yu simvolov budet,
k primeru,
Takie iskusstvennye yazyki polezny dlya formulirovki prostyh zadach i primerov
razlichnyh vozmozhnostei. My mozhem takzhe priblizhenno opisat' nekotoryi
estestvennyi yazyk seriei prostyh iskusstvennyh. Nulevym priblizheniem takogo roda
budet model' s ravnoveroyatnymi nezavisimymi bukvami, sleduyushim shagom mozhet
sluzhit' uchet razlichnyh veroyatnostei bukv v estestvennom yazyke
(Veroyatnosti bukv, digramm i trigramm dayutsya v
Secret and Urgent by Fletcher Pratt, Blue Ribbon Books, 1939.
Chastoty vstrechaemosti otdel'nyh slov privedeny v Relative Frequency of English
Speech Sounds, G. Dewey, Harvard University Press, 1923.).
Tak, v pervom priblizhenii dlya angliiskogo yazyka bukva E budet vybirat'sya
s veroyatnost'yu 0.12, a W - 0.02, no ne budet nikakogo vliyaniya bukv drug
na druga, i ne budet zametna tendenciya k obrazovaniyu naibolee chastyh bukvosochetanii,
takih kak TH ili ED. Vo vtorom priblizhenii neobhodimo uchest'
strukturu digramm - posle vybora odnoi iz bukv sleduyushaya vybiraetsya uzhe soglasno
sootvetstvuyushei uslovnoi veroyatnosti, chto trebuet znaniya chastoty digramm ![]() .
Na sleduyushem shage vvoditsya struktura trigramm - kazhdaya bukva zavisit uzhe
ot dvuh predshestvuyushih.
.
Na sleduyushem shage vvoditsya struktura trigramm - kazhdaya bukva zavisit uzhe
ot dvuh predshestvuyushih.
Postepennoe priblizhenie k angliiskomu yazyku
Dlya illyustracii togo, kak eta seriya priblizhenii opisyvaet estestvennyi yazyk, byli postroeny tipichnye posledovatel'nosti priblizhenii dlya angliiskogo yazyka. Vo vseh sluchayah ispol'zovalsya 27-simvol'nyi ``alfavit'' - 26 bukv i probel.
-
Nulevoe priblizhenie (simvoly nezavisimy i ravnoveroyatny).
XFOML RXKHRJFFJUJ ZLPWCFWKCYJ FFJEYVKCQSGHYD QPAAMKBZAACIBZLHJQD.
-
Pervoe priblizhenie (simvoly nezavisimy, no chastoty iz sootvetstvuyut angliiskomu
tekstu).
OCRO HLI RGWR NMIELWIS EU LL NBNESEBYA TH EEI ALHENHTTPA OOBTTVA NAH BRL.
-
Vtoroe priblizhenie (uchtena digrammnaya struktura angliiskogo yazyka).
ON IE ANTSOUTINYS ARE T INCTORE ST BE S DEAMY ACHIN D ILONASIVE TUCOOWE AT TEASONARE FUSO TIZIN ANDY TOBE SEACE CTISBE.
-
Tret'e priblizhenie (uchtena trigrammnaya struktura).
IN NO IST LAT WHEY CRATICT FROURE BIRS GROCID PONDENOME OF DEMONSTURES OF THE REPTAGIN IS REGOACTIONA OF CRE.
-
Chetvertoe priblizhenie. Vmesto dal'neishego ispol'zovaniya tetragramm,
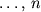 -gramm
proshe pereiti k slovarnoi strukture. V dannom priblizhenii slova nezavisimy,
no ih chastoty sootvetstvuyut angliiskomu tekstu.
-gramm
proshe pereiti k slovarnoi strukture. V dannom priblizhenii slova nezavisimy,
no ih chastoty sootvetstvuyut angliiskomu tekstu.
REPRESENTING AND SPEEDILY IS AN GOOD APT OR COME CAN DIFFERENT NATURAL HERE HE THE A IN CAME THE TO OF TO EXPERT GRAY COME TO FURNISHES THE LINE MESSAGE HAD BE THESE.
-
Priblizhenie vtorogo poryadka s ispol'zovaniem slov - uchteny ih veroyatnosti perehoda.
THE HEAD AND IN FRONTAL ATTACK ON AN ENGLISH WRITER THAT THE CHARACTER OF THIS POINT IS THEREFORE ANOTHER METHOD FOR THE LETTERS THAT THE TIME OF WHO EVER TOLD THE PROBLEM FOR AN UNEXPECTED.
S kazhdym shagom zametno vozrastaet shodstvo s angliiskim yazykom. Zametim, chto privedennye primery sohranyayut dostatochno pohozhuyu na original strukturu i daleko za ramkami sootvetstvuyushego priblizheniya. Tak, vtoroe priblizhenie daet priemlemyi tekst na urovne dvuhbukvennyh sochetanii, no chetyrehbukvennye kombinacii v nem takzhe yavlyayutsya dostatochno shozhimi s angliiskim yazykom; figuriruyushie v poslednem primere kombinacii chetyreh i bolee slov takzhe vpolne mogut vstrechat'sya v real'nyh predlozheniyah. Tak, fraza iz 10 slov ``attack on an English writer that the character of this'' ne yavlyaetsya sovsem uzh bessmyslennoi. Vidno, chto dostatochno slozhnyi stohasticheskii process mozhet yavlyat'sya vpolne udovletvoritel'noi model'yu diskretnogo istochnika.
Dva pervyh primera postroeny s ispol'zovaniem knigi sluchainyh chisel i tablicy chastot bukv. Pohozhii metod mozhno bylo by ispol'zovat' i dlya posleduyushih, tak kak chastoty digramm i trigramm izvestny, odnako my vospol'zovalis' inym, bolee prostym podhodom. Dlya postroeniya vtorogo priblizheniya, naprimer, otkryvalas' sluchainym obrazom kniga i vybiralas' sluchainaya bukva, kotoraya zapisyvalas'; zatem kniga otkryvalas' na drugoi stranice i iskalas' pervaya dvuhbukvennaya kombinaciya, nachinayushayasya s uzhe otobrannoi bukvy, i zapisyvalas' sleduyushaya bukva. Zatem procedura povtoryalas'. Pohozhii podhod ispol'zovalsya i dlya ostal'nyh primerov. Bylo by interesnym postroit' takzhe i sleduyushie priblizheniya, odnako eto trebuet slishkom bol'shih zatrat vremeni i sil.
Predstavlenie markovskogo processa v vide grafa
Stohasticheskie processy opisannogo vyshe tipa v matematike izvestny kak
markovskie processy i dostatochno shiroko osvesheny v literature
(za podrobnym izlozheniem otsylaem chitatelya k knige M. Frechet,
Methode des fonctions arbitraires. Theorie des evenements
en chane dans le cas d'un nombre fini d'etats possibles, Paris,
Gauthier-Villars, 1938.). V obshem sluchae ih mozhno opisat' sleduyushim
obrazom. Sushestvuet konechnoe chislo vozmozhnyh sostoyanii sistemy ![]() ,
krome togo, izvesten nabor veroyatnostei perehoda
,
krome togo, izvesten nabor veroyatnostei perehoda ![]() sistemy
iz sostoyaniya
sistemy
iz sostoyaniya ![]() v sostoyanie
v sostoyanie ![]() . Chtoby sdelat'
takoi markovskii process istochnikom informacii, dostatochno predpolozhit', chto
on vydaet po odnoi bukve v moment kazhdogo perehoda. Razlichnye sostoyaniya sistemy
v takom sluchae sootvetstvuyut ``ostatochnomu vliyaniyu'' predshestvuyushih bukv.
. Chtoby sdelat'
takoi markovskii process istochnikom informacii, dostatochno predpolozhit', chto
on vydaet po odnoi bukve v moment kazhdogo perehoda. Razlichnye sostoyaniya sistemy
v takom sluchae sootvetstvuyut ``ostatochnomu vliyaniyu'' predshestvuyushih bukv.
Etu situaciyu mozhno predstavit' v vide grafov, kak pokazano na ris.3, 4 i 5.

Ris.3. Graf, sootvetstvuyushii istochniku iz primera B.
Sostoyaniya zdes' predstavleny vershinami grafa, a veroyatnosti i sootvetstvuyushie im bukvy privedeny ryadom s sootvetstvuyushimi liniyami perehodov. Ris. 3 sootvetstvuet primeru (B) glavy 2, a ris. 4 - primeru (C)

Ris.4. Graf, sootvetstvuyushii istochniku iz primera C.
U sistemy, izobrazhennoi na ris. 3, est' lish' odno sostoyanie, tak kak vybiraemye
bukvy nezavisimy. Na ris. 4 chislo sostoyanii ravno chislu bukv; v sluchae
ucheta trigrammnoi struktury ih chislo ravno ![]() , chto sootvetstvuet
vozmozhnym param predshestvuyushih bukv. Na ris. 5 izobrazhen graf, sootvetstvuyushii
strukture slov iz primera (D) (S oboznachaet simvol probela).
, chto sootvetstvuet
vozmozhnym param predshestvuyushih bukv. Na ris. 5 izobrazhen graf, sootvetstvuyushii
strukture slov iz primera (D) (S oboznachaet simvol probela).
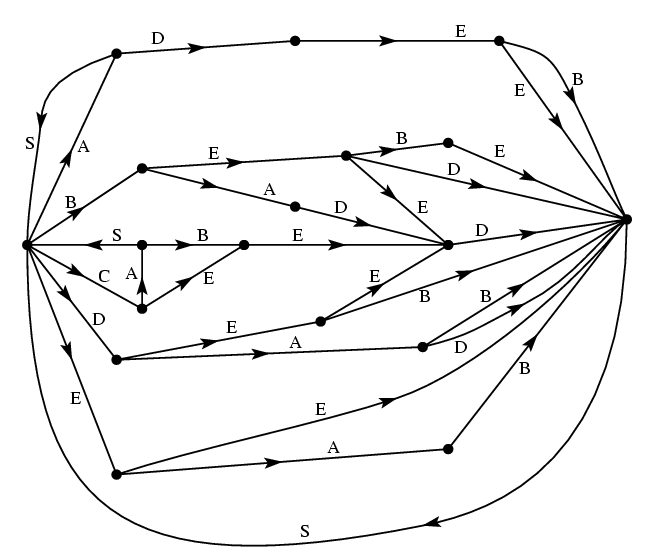
Ris.5. Graf, sootvetstvuyushii istochniku iz primera D.
Ergodicheskie i smeshannye istochniki
Kak uzhe bylo otmecheno, diskretnyi istochnik v nashih zadachah mozhet rassmatrivat'sya kak markovskii process. Sredi vseh vozmozhnyh markovskih processov mozhno vydelit' gruppu so svoistvami, vazhnymi dlya teorii svyazi. V etot klass vhodyat tak nazyvaemye ``ergodicheskie'' processy, i my budem nazyvat' sootvetstvuyushie istochniki ergodicheskimi. Hotya strogoe opredelenie ergodicheskogo processa dostatochno zaputanno, osnovnaya ideya prosta. Dlya ergodicheskogo processa vse sgenerirovannye posledovatel'nosti obladayut odinakovymi statisticheskimi svoistvami, to est', k primeru, chastoty vstrechaemosti bukv, digramm i tek dalee, ocenennye po otdel'nym posledovatel'nostyam, shodyatsya s rostom dliny vyborok k opredelennym predelam, ne zavisyashim ot posledovatel'nosti. Na samom dele eto verno ne dlya vsyakoi posledovatel'nosti, odnako mnozhestvo posledovatel'nostei, dlya kotoryh eto ne vypolnyaetsya, imeet meru nol' (to est' obladaet nulevoi veroyatnost'yu). Grubo svoistvo ergodichnosti oznachaet statisticheskuyu odnorodnost'.
Vse vysheprivedennye primery iskusstvennyh yazykov yavlyayutsya ergodicheskimi. Eto svyazano so strukturoi sootvetstvuyushih grafov. Esli graf obladaet dvumya sleduyushimi svoistvami, sootvetstvuyushii process budet ergodicheskim:
- Graf ne sostoit iz dvuh izolirovannyh chastei A i B, takih, chto nevozmozhno pereiti s vershin odnoi chasti na vershiny drugoi po liniyam grafa v razreshennom napravlenii, i s vershin vtoroi - na vershiny pervoi.
- Nazovem zamknutye serii reber grafa, kotorye mozhno oboiti v razreshennom napravlenii, ``konturom''. Dlinoi kontura nazovem chislo reber v nem. Togda na ris. 5 seriya reber BEBES obrazuet kontur dliny 5. Vtorym trebuemym svoistvom yavlyaetsya ravenstvo naibol'shego obshego delitelya dlin vseh konturov na grafe edinice.
Esli vypolnyaetsya tol'ko pervoe iz uslovii, a vtoroe narusheno, t.e. naibol'shii
obshii delitel' raven ![]() , posledovatel'nost' imeet nekotoruyu
periodicheskuyu strukturu. Razlichnye posledovatel'nosti raspadayutsya na
, posledovatel'nost' imeet nekotoruyu
periodicheskuyu strukturu. Razlichnye posledovatel'nosti raspadayutsya na ![]() statisticheski ravnoznachnyh klassov, otlichayushihsya lish' sdvigom nachala (to est'
tem, kakaya imenno bukva nazyvaetsya pervoi). Sdvigom ot 0 do
statisticheski ravnoznachnyh klassov, otlichayushihsya lish' sdvigom nachala (to est'
tem, kakaya imenno bukva nazyvaetsya pervoi). Sdvigom ot 0 do ![]() lyubaya iz etih posledovatel'nostei mozhet byt' sdelana statisticheski ekvivalentnoi
lyuboi drugoi. Prostym primerom s
lyubaya iz etih posledovatel'nostei mozhet byt' sdelana statisticheski ekvivalentnoi
lyuboi drugoi. Prostym primerom s ![]() mozhet sluzhit' sluchai s
tremya bukvami
mozhet sluzhit' sluchai s
tremya bukvami ![]() . Za bukvoi
. Za bukvoi ![]() sleduet libo
sleduet libo ![]() , libo
, libo ![]() s veroyatnostyami
s veroyatnostyami ![]() i
i ![]() sootvetstvenno.
Za bukvami zhe
sootvetstvenno.
Za bukvami zhe ![]() ili
ili ![]() vsegda sleduet
vsegda sleduet ![]() .
Togda tipichnoi posledovatel'nost'yu budet
.
Togda tipichnoi posledovatel'nost'yu budet
a b a c a c a c a b a c a b a b a c a c.
Dannyi sluchai ne ochen' vazhen dlya nashei raboty.
Esli zhe narushaetsya pervoe uslovie, graf raspadaetsya na neskol'ko podgrafov,
na kazhdom iz kotoryh eto uslovie vypolneno. My budem predpolagat', chto na
kazhdom iz nih vypolneno takzhe i vtoroe uslovie. V eto sluchae my imeem
``smeshannyi'' istochnik, sostoyashii iz neskol'kih chistyh, sootvetstvuyushih
kazhdomu iz subgrafov. Esli ![]() ,
, ![]() ,
, ![]() -
chistye komponenty, mozhno zapisat'
-
chistye komponenty, mozhno zapisat'
gde ![]() - veroyatnost' komponenta istochnika
- veroyatnost' komponenta istochnika ![]() .
.
Fizicheski situaciya predstavlyaet iz sebya sleduyushee. Est' neskol'ko razlichnyh
istochnikov ![]() ,
, ![]() ,
, ![]() , kazhdyi
iz kotoryh statisticheski odnoroden (t.e. ergodichen). My ne mozhem skazat'
a priori, kotoryi iz nih budet ispol'zovan, no esli
posledovatel'nost' nachinaetsya v kakom-to iz chistyh komponentov, v dal'neishem
ona v nem i ostanetsya, beskonechno prodolzhayas' v sootvetstvii s ego statisticheskoi
strukturoi.
, kazhdyi
iz kotoryh statisticheski odnoroden (t.e. ergodichen). My ne mozhem skazat'
a priori, kotoryi iz nih budet ispol'zovan, no esli
posledovatel'nost' nachinaetsya v kakom-to iz chistyh komponentov, v dal'neishem
ona v nem i ostanetsya, beskonechno prodolzhayas' v sootvetstvii s ego statisticheskoi
strukturoi.
Dlya primera voz'mem dva iz vysheprivedennyh processov i primem ![]() i
i ![]() .
Posledovatel'nost' ot smeshannogo istochnika
.
Posledovatel'nost' ot smeshannogo istochnika
mozhet byt' poluchena vyborom ![]() libo
libo ![]() s veroyatnostyami
0.2 i 0.8 i generirovaniem posledovatel'nosti v sootvetstviem s etim vyborom.
s veroyatnostyami
0.2 i 0.8 i generirovaniem posledovatel'nosti v sootvetstviem s etim vyborom.
V dal'neishem my budet predpolagat' istochnik ergodicheskim, esli special'no ne ukazano obratnoe. Eto predpolozhenie pozvolyaet otozhdestvit' srednie po posledovatel'nosti so srednimi po ansamblyu vseh vozmozhnyh posledovatel'nostei (veroyatnost' otlichiya ravna nulyu). K primeru, otnositel'naya chastota bukvy A v nekotoroi beskonechnoi posledovatel'nosti s veroyatnost'yu edinica budet ravna otnositel'noi chastote ee v ansamble posledovatel'nostei.
Esli ![]() - veroyatnost' sostoyaniya
- veroyatnost' sostoyaniya ![]() i
i ![]() -
veroyatnost' perehoda v v sostoyanie
-
veroyatnost' perehoda v v sostoyanie ![]() , yasno, chto dlya stacionarnosti processa
, yasno, chto dlya stacionarnosti processa
![]() dolzhna udovletvoryat' usloviyu ravnovesiya:
dolzhna udovletvoryat' usloviyu ravnovesiya:
V ergodicheskom sluchae mozhno pokazat', chto pri lyubyh nachal'nyh usloviyah
veroyatnosti ![]() okazat'sya v sostoyanii
okazat'sya v sostoyanii ![]() posle
posle
![]() simvolov stremyatsya k ravnovesnomu znacheniyu pri
simvolov stremyatsya k ravnovesnomu znacheniyu pri ![]() .
.
Vybor, neopredelennost' i entropiya
My predstavili diskretnyi istochnik informacii markovskim processom. Mozhem li my opredelit' nekotoruyu velichinu, harakterizuyushuyu v nekotorom smysle kolichestvo informacii, ``proizvodimoi'' takim processom, ili, tochnee, temp ``proizvodstva'' informacii?
Pust' u nas est' nabor vozmozhnyh sobytii s veroyatnostyami ![]() .
Eti veroyatnosti izvestny i bol'she pro eti sobytiya nichego ne izvestno.
Mozhno li naiti meru sovershaemogo ``vybora'' odnogo iz sobytii ili zhe
neopredelennosti poluchaemogo rezul'tata?
.
Eti veroyatnosti izvestny i bol'she pro eti sobytiya nichego ne izvestno.
Mozhno li naiti meru sovershaemogo ``vybora'' odnogo iz sobytii ili zhe
neopredelennosti poluchaemogo rezul'tata?
Razumno potrebovat' ot takoi mery, skazhem, ![]() , sleduyushih svoistv:
, sleduyushih svoistv:
-
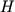 dolzhna byt' nepreryvna po
dolzhna byt' nepreryvna po 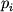 .
.
-
V sluchae ravenstva vseh
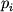 ,
, 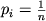 ,
,
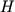 dolzhna byt' monotonno vozrastayushei funkciei
dolzhna byt' monotonno vozrastayushei funkciei 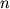 .
Dlya ravnoveroyatnyh sobytii neopredelennost', ili vozmozhnost' vybora, vozrastaet
s rostom chisla vozmozhnyh sobytii.
.
Dlya ravnoveroyatnyh sobytii neopredelennost', ili vozmozhnost' vybora, vozrastaet
s rostom chisla vozmozhnyh sobytii.
-
Pri razbienii odnogo iz vozmozhnyh vyborov na dva, ishodnaya velichina
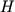 dolzhna byt' vzveshennoi summoi otdel'nyh velichin
dolzhna byt' vzveshennoi summoi otdel'nyh velichin 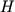 . Smysl etogo
illyustriruetsya na ris. 6.
. Smysl etogo
illyustriruetsya na ris. 6.
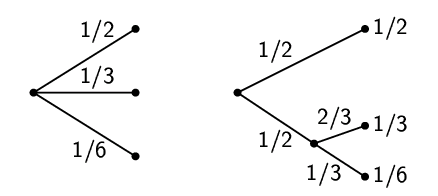
Ris.6. Razlozhenie vybora iz treh vozmozhnostei.Sleva my imeem tri vozmozhnosti
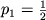 ,
, 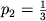 ,
, 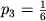 . Sprava, my snachala vybiraem
mezhdu dvumya vozmozhnostyami veroyatnost'yu
. Sprava, my snachala vybiraem
mezhdu dvumya vozmozhnostyami veroyatnost'yu 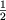 kazhdaya, i, v sluchae
vybora vtoroi, delaem sleduyushii vybor s veroyatnostyami
kazhdaya, i, v sluchae
vybora vtoroi, delaem sleduyushii vybor s veroyatnostyami 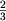 ,
,
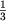 . Konechnye rezul'taty imeyut te zhe veroyatnosti, chto
i ran'she. V dannom konkretnom sluchae trebovanie svoditsya k
. Konechnye rezul'taty imeyut te zhe veroyatnosti, chto
i ran'she. V dannom konkretnom sluchae trebovanie svoditsya k
Koefficient
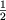 voznikaet iz-za togo, chto vtoroi vybor
delaetsya lish' v polovine sluchaev.
voznikaet iz-za togo, chto vtoroi vybor
delaetsya lish' v polovine sluchaev.
V prilozhenii 2 dokazyvaetsya sleduyushii rezul'tat:
Teorema 2: Edinstvennaya $H$, udovletvoryayushaya trem vysheprivedennym usloviyam, imeet vid:
gde ![]() - nekotoraya polozhitel'naya konstanta.
- nekotoraya polozhitel'naya konstanta.
Eta teorema, kak i predpolozheniya, trebuemye dlya ee dokazatel'stva, nikak ne budut ispol'zovat'sya v dal'neishem. Oni privedeny glavnym obrazom dlya pridaniya nekotoroi pravdopodobnosti nashim posleduyushim opredeleniyam. Ih istinnym dokazatel'stvom, odnako, posluzhat ih prilozheniya.
Velichiny vida ![]() (konstanta
(konstanta ![]() otvechaet za vybor sistemy edinic) igrayut central'nuyu rol' v teorii informacii
kak mery informacii, vybora i neopredelennosti. Takoi zhe vid imeet vyrazhenie
dlya entropii v nekotoryh formulirovkah statisticheskoi mehaniki (sm., k primeru,
R. C. Tolman, Principles of Statistical Mechanics,
Oxford, Clarendon, 1938.), gde
otvechaet za vybor sistemy edinic) igrayut central'nuyu rol' v teorii informacii
kak mery informacii, vybora i neopredelennosti. Takoi zhe vid imeet vyrazhenie
dlya entropii v nekotoryh formulirovkah statisticheskoi mehaniki (sm., k primeru,
R. C. Tolman, Principles of Statistical Mechanics,
Oxford, Clarendon, 1938.), gde ![]() - veroyatnost' naiti
sistemu v yacheike
- veroyatnost' naiti
sistemu v yacheike ![]() ee fazovogo prostranstva.
ee fazovogo prostranstva. ![]() togda,
k primeru, sovpadaet s
togda,
k primeru, sovpadaet s ![]() v znamenitoi teoreme Bol'cmana.
Nazovem
v znamenitoi teoreme Bol'cmana.
Nazovem ![]() entropiei nabora veroyatnostei
entropiei nabora veroyatnostei ![]() .
Budem oboznachat'
.
Budem oboznachat' ![]() entropiyu sluchainoi velichiny
entropiyu sluchainoi velichiny ![]() ;
zdes'
;
zdes' ![]() - ne argument funkcii, a metka, prizvannaya otlichat'
oboznachenie entropii velichiny
- ne argument funkcii, a metka, prizvannaya otlichat'
oboznachenie entropii velichiny ![]() ot entropii
ot entropii ![]() sluchainoi velichiny
sluchainoi velichiny ![]() .
.
Entropiya dlya sluchaya dvuh vozmozhnostei s veroyatnostyami ![]() i
i
![]() ,
,
izobrazhena na ris. 7 kak funkciya ![]() .
.

Ris.7. Entropiya dlya sluchaya dvuh vozmozhnostei s veroyatnostyami
Velichina ![]() obladaet neskol'kimi interesnymi svoistvami,
delayushimi ee priemlemoi meroi vybora ili informacii:
obladaet neskol'kimi interesnymi svoistvami,
delayushimi ee priemlemoi meroi vybora ili informacii:
1. ![]() togda i tol'ko togda, kogda vse
togda i tol'ko togda, kogda vse ![]() za isklyucheniem odnogo ravny nulyu, a odin - edinice, to est' velichina
za isklyucheniem odnogo ravny nulyu, a odin - edinice, to est' velichina
![]() obrashaetsya v nol' lish' togda, kogda my uvereny v vybore.
Vo vseh ostal'nyh sluchayah
obrashaetsya v nol' lish' togda, kogda my uvereny v vybore.
Vo vseh ostal'nyh sluchayah ![]() polozhitel'na.
polozhitel'na.
2. Dlya dannogo ![]()
![]() prinimaet maksimal'noe znachenie
togda, kogda vse $p_i$ ravny mezhdu soboi (i, sootvetstvenno,
ravny
prinimaet maksimal'noe znachenie
togda, kogda vse $p_i$ ravny mezhdu soboi (i, sootvetstvenno,
ravny ![]() ). Intuitivno ponyatno, chto eto - naibolee neopredelennaya
situaciya.
). Intuitivno ponyatno, chto eto - naibolee neopredelennaya
situaciya.
3. Rassmotrim dva sobytiya, ![]() i
i ![]() , prichem
pervomu sootvetstvuet
, prichem
pervomu sootvetstvuet ![]() vozmozhnostei, a vtoromu -
vozmozhnostei, a vtoromu - ![]() .
Pust'
.
Pust' ![]() - veroyatnost' sovmestnogo poyavleniya
- veroyatnost' sovmestnogo poyavleniya ![]() dlya
pervogo i
dlya
pervogo i ![]() dlya vtorogo. Entropiya takogo sovmestnogo sobytiya ravna
dlya vtorogo. Entropiya takogo sovmestnogo sobytiya ravna
v to vremya kak
Legko pokazat', chto
prichem ravenstvo dostigaetsya lish' pri nezavisimosti sobytii (t.e. pri ![]() ). Neopredelennost' sovmestnogo sobytiya men'she ili ravna summe
neopredelennostei sobytii po-otdel'nosti.
). Neopredelennost' sovmestnogo sobytiya men'she ili ravna summe
neopredelennostei sobytii po-otdel'nosti.
4. Lyuboe izmenenie, napravlennoe na uravnivanie veroyatnostei ![]() , uvelichivaet
, uvelichivaet ![]() . Tak, esli
. Tak, esli ![]() i my
uvelichivaem
i my
uvelichivaem ![]() , umen'shaya
, umen'shaya ![]() na tu zhe velichinu,
tak chto
na tu zhe velichinu,
tak chto ![]() i
i ![]() okazyvayutsya blizhe brug k drugu,
velichina
okazyvayutsya blizhe brug k drugu,
velichina ![]() vozrastaet. V bolee obshem sluchae, esli my proizvodim
nekotoruyu proceduru ``usredneniya''
vozrastaet. V bolee obshem sluchae, esli my proizvodim
nekotoruyu proceduru ``usredneniya'' ![]() vida
vida
gde ![]() i vse
i vse ![]() ,
velichina
,
velichina ![]() vozrastaet (za isklyucheniem special'nogo sluchaya, pri kotorom
znacheniya
vozrastaet (za isklyucheniem special'nogo sluchaya, pri kotorom
znacheniya ![]() prosto menyayutsya mestami; v etom sluchae $H$, estestvenno, ostaetsya
neizmennoi).
prosto menyayutsya mestami; v etom sluchae $H$, estestvenno, ostaetsya
neizmennoi).
5.Rassmotrim dva sluchainyh sobytiya, ![]() i
i ![]() , kak v
punkte 3, ne obyazatel'no nezavisimyh. Dlya lyubogo znacheniya
, kak v
punkte 3, ne obyazatel'no nezavisimyh. Dlya lyubogo znacheniya ![]() , kotoroe
mozhet prinimat'
, kotoroe
mozhet prinimat' ![]() , sushestvuet uslovnaya veroyatnost'
, sushestvuet uslovnaya veroyatnost' ![]() togo, chto
togo, chto ![]() primet znachenie
primet znachenie ![]() . Ona imeet vid
. Ona imeet vid
Opredelim uslovnuyu entropiyu velichiny ![]() ,
, ![]() ,
kak srednyuyu entropiyu
,
kak srednyuyu entropiyu ![]() pri kazhdom znachenii
pri kazhdom znachenii ![]() , vzveshennuyu
v sootvetstvii s veroyatnost'yu polucheniya dannogo znacheniya
, vzveshennuyu
v sootvetstvii s veroyatnost'yu polucheniya dannogo znacheniya ![]() . Ona ravna
. Ona ravna
Eto velichina pokazyvaet, naskol'ko v srednem yavlyaetsya neopredelennoi ![]() ,
esli my znaem
,
esli my znaem ![]() . Podstavlyaya
. Podstavlyaya ![]() , poluchaem
, poluchaem
ili
Neopredelennost' (ili entropiya) sovmestnogo sobytiya ![]() ravna
summe neopredelennosti
ravna
summe neopredelennosti ![]() i neopredelennosti
i neopredelennosti ![]() pri
izvestnoi velichine
pri
izvestnoi velichine ![]() .
.
6. Iz punktov 3 i 5 imeem
Takim obrazom,
Neopredelennost' ![]() nikogda ne uvelichivaetsya pri konkretizacii
nikogda ne uvelichivaetsya pri konkretizacii ![]() .
Ona umen'shaetsya, esli tol'ko
.
Ona umen'shaetsya, esli tol'ko ![]() i
i ![]() ne yavlyayutsya nezavisimymi
sobytiyami. V poslednem zhe sluchae ona ostaetsya neizmennoi.
ne yavlyayutsya nezavisimymi
sobytiyami. V poslednem zhe sluchae ona ostaetsya neizmennoi.
Entropiya istochnika informacii
Rassmotrim diskretnyi istochnik informacii opisannogo vyshe tipa. Dlya kazhdogo
iz sostoyanii ![]() sushestvuet nabor veroyatnostei
sushestvuet nabor veroyatnostei ![]() generacii razlichnyh vozmozhnyh simvolov
generacii razlichnyh vozmozhnyh simvolov ![]() , chto sootvetstvuet
entorpii dannogo sostoyaniya
, chto sootvetstvuet
entorpii dannogo sostoyaniya ![]() . Opredelim entropiyu istochnika
kak srednee vseh
. Opredelim entropiyu istochnika
kak srednee vseh ![]() , vzveshennyh soglasno veroyatnostyam
sootvetstvuyushih sostoyanii:
, vzveshennyh soglasno veroyatnostyam
sootvetstvuyushih sostoyanii:
Eto entropiya v raschete na simvol teksta. Esli markovskii process imeet opredelennyi temp, mozhno takzhe opredelit' entrpoiyu v sekundu
shde ![]() - srednyaya chastota (realizacii v sekundu) sostoyaniya
- srednyaya chastota (realizacii v sekundu) sostoyaniya
![]() . Yasno, chto
. Yasno, chto
gde ![]() - srednee chislo simvolov, generiruemyh za sekundu.
- srednee chislo simvolov, generiruemyh za sekundu.
![]() ili
ili ![]() harakterizuyut kolichestvo informacii,
proizvodimoi istochnikom v raschete na simvol ili na sekundu. Esli za osnovanie
logarifma prinyata dvoika, oni predstavlyayut soboi bity na simvol ili bity v sekundu.
harakterizuyut kolichestvo informacii,
proizvodimoi istochnikom v raschete na simvol ili na sekundu. Esli za osnovanie
logarifma prinyata dvoika, oni predstavlyayut soboi bity na simvol ili bity v sekundu.
Esli posledovatel'nye simvoly nezavisimy, to ![]() est' prosto
est' prosto ![]() , gde
, gde ![]() - veroyatnost' simvola
- veroyatnost' simvola ![]() .
Pust' my imeem dostatochno dlinnoe soobshenie, soderzhashee
.
Pust' my imeem dostatochno dlinnoe soobshenie, soderzhashee ![]() simvolov.
S vysokoi veroyatnost'yu v nem budet primerno
simvolov.
S vysokoi veroyatnost'yu v nem budet primerno ![]() vhozhdenii pervogo
simvola,
vhozhdenii pervogo
simvola, ![]() - vtorogo, i tak dalee. Takim obrazom veroyatnost'
dannogo sobsheniya budet primerno ravna
- vtorogo, i tak dalee. Takim obrazom veroyatnost'
dannogo sobsheniya budet primerno ravna
ili zhe
![]() , takim obrazom, est' logarifm obratnoi veroyatnosti tipichnoi
dlinnoi posledovatel'nosti, delennyi na chislo simvolov v nei. Analogichnyi
rezul'tat imeet mesto dlya proizvol'nogo istochnika. Bolee tochno, mozhno
sformuliovat' (sm. prilozhenie 3)
, takim obrazom, est' logarifm obratnoi veroyatnosti tipichnoi
dlinnoi posledovatel'nosti, delennyi na chislo simvolov v nei. Analogichnyi
rezul'tat imeet mesto dlya proizvol'nogo istochnika. Bolee tochno, mozhno
sformuliovat' (sm. prilozhenie 3)
Teorema 3: Dlya proizvol'nyh ![]() i
i ![]() mozhno naiti takoe
mozhno naiti takoe ![]() , chto posledovatel'nosti proizvol'noi dliny
, chto posledovatel'nosti proizvol'noi dliny
![]() raspadayutsya na dva klassa:
raspadayutsya na dva klassa:
![]() .
.
Inymi slovami, prakticheski navernyaka dostatochno
blizko k ![]() pri dostatochno bol'shih
pri dostatochno bol'shih ![]() .
.
Pohozhii rezul'tat imeet mesto dlya chisla posledovatel'nostei s razlichnymi
veroyatnostyami. Rassmotrim vnov' posledovatel'nosti dliny ![]() i
otsortiruem ih po ubyvaniyu veroyatnosti. Opredelim
i
otsortiruem ih po ubyvaniyu veroyatnosti. Opredelim ![]() kak chislo
posldovatel'nostei, kotorye my dolzhny vybrat' iz dannogo nabora, nachinaya s naibolee
veroyatnoi, dlya polucheniya summarnoi veroyatnosti
kak chislo
posldovatel'nostei, kotorye my dolzhny vybrat' iz dannogo nabora, nachinaya s naibolee
veroyatnoi, dlya polucheniya summarnoi veroyatnosti ![]() .
.
Teorema 4:
pri ![]() , ne ravnyh
, ne ravnyh ![]() ili
ili ![]() .
.
![]() mozhet byt' istolkovano kak chislo bit, trebuemyh dlya
vydeleniya posledovatel'nosti, esli my rassmatrivaem lish' naibolee veroyatnye
iz nih summarnoi veroyatnost'yu
mozhet byt' istolkovano kak chislo bit, trebuemyh dlya
vydeleniya posledovatel'nosti, esli my rassmatrivaem lish' naibolee veroyatnye
iz nih summarnoi veroyatnost'yu ![]() . Togda -
chislo bin na simvol dlya takogo vydeleniya. Teorema glasit, chto dlya bol'shih
. Togda -
chislo bin na simvol dlya takogo vydeleniya. Teorema glasit, chto dlya bol'shih
![]() ono ne zavisit ot
ono ne zavisit ot ![]() i ravno
i ravno ![]() . Temp
rosta logarifma chisla dostatochno veroyatnyh posledovatel'nostei daetsya
. Temp
rosta logarifma chisla dostatochno veroyatnyh posledovatel'nostei daetsya ![]() vne zavisimosti ot togo, kak imenno my opredelyaem etu ``dostatochnuyu veroyatnost'''.
Blagodarya etim rezul'tatam (dokazyvaemym v prilozhenii 3) dlya bol'shinstva zadach
mozhno schitat', chto (dostatochno dlinnyh) posledovatel'nostei vsego
vne zavisimosti ot togo, kak imenno my opredelyaem etu ``dostatochnuyu veroyatnost'''.
Blagodarya etim rezul'tatam (dokazyvaemym v prilozhenii 3) dlya bol'shinstva zadach
mozhno schitat', chto (dostatochno dlinnyh) posledovatel'nostei vsego ![]() ,
i kazhdaya iz nih imeet veroyatnost'
,
i kazhdaya iz nih imeet veroyatnost' ![]() .
.
Dve sleduyushih teoremy pokazyvayut, chto ![]() i
i ![]() mogut
byt' opredeleny posredstvom predelnyh perehodov pryamo iz statistiki soobsheniya,
bez konkretizacii razlichnyh sostoyanii i veroyatnostei perehoda.
mogut
byt' opredeleny posredstvom predelnyh perehodov pryamo iz statistiki soobsheniya,
bez konkretizacii razlichnyh sostoyanii i veroyatnostei perehoda.
Teorema 5:
Pust' ![]() - veroyatnost' posledovatel'nosti simvolov
- veroyatnost' posledovatel'nosti simvolov ![]() ot istochnika, i pust'
ot istochnika, i pust'
gde summirovanie proizvoditsya po vsem posledovatel'nostyam ![]() , soderzhashim
, soderzhashim
![]() simvolov. Togda
simvolov. Togda ![]() - monotonno ubyvayushaya funkciya
- monotonno ubyvayushaya funkciya
![]() i
i
Teorema 6:
Pust' ![]() - veroyatnost' togo, chto za posledovatel'nost'yu
- veroyatnost' togo, chto za posledovatel'nost'yu
![]() sleduet simvol
sleduet simvol ![]() , i
, i ![]() -
uslovnaya veroyatnost'
-
uslovnaya veroyatnost' ![]() posle
posle ![]() . Pust'
. Pust'
gde summirovanie proizvoditsya po vsem blokam ![]() dlinoi
dlinoi ![]() simvolov
i po vsem simvolam
simvolov
i po vsem simvolam ![]() . Togda
. Togda ![]() - monotonno ubyvayushaya
funkciya
- monotonno ubyvayushaya
funkciya ![]() ,
,
i ![]() .
.
Eti rezul'taty poluchayutsya v prilozhenii 3. Oni pokazyvayut, chto seriya priblizhenii
k ![]() mozhet byt' poluchena pri rassmotrenii statisticheskoi struktury
posledovatel'nostei dlinoi
mozhet byt' poluchena pri rassmotrenii statisticheskoi struktury
posledovatel'nostei dlinoi ![]() simvolov.
simvolov. ![]() yavlyaetsya nailuchshim priblizheniem. Fakticheski
yavlyaetsya nailuchshim priblizheniem. Fakticheski ![]() yavlyaetsya entropiei
yavlyaetsya entropiei
![]() -togo priblizheniya dlya istochnika, opisannogo vyshe tipa. Esli
statisticheskoe vliyanie na rasstoyaniyah, bol'shih
-togo priblizheniya dlya istochnika, opisannogo vyshe tipa. Esli
statisticheskoe vliyanie na rasstoyaniyah, bol'shih ![]() , otsutstvuet,
to est' esli uslovnaya veroyatnost' posleduuyushego simvola pri znanii
, otsutstvuet,
to est' esli uslovnaya veroyatnost' posleduuyushego simvola pri znanii ![]() predydushego ne izmenyaetsya konkretizaciei lyubogo predshestvuyushego im, to
predydushego ne izmenyaetsya konkretizaciei lyubogo predshestvuyushego im, to ![]() .
.
![]() , estestvenno, yavletsya uslovnoi entropiei posleduyushego simvoda pri
znanii
, estestvenno, yavletsya uslovnoi entropiei posleduyushego simvoda pri
znanii ![]() predydushih, togda kak $G_N$ - entropiya na simvol
blokov dliny $N$.
predydushih, togda kak $G_N$ - entropiya na simvol
blokov dliny $N$.
Nazovem otnoshenie entropii istochnika k maksimal'nomu znacheniyu, kotoroe ona
mozhet prinimat', buduchi ogranichennoi temi zhe predshestvuyushimi simvolami,
otnositel'noi entropiei. Eto - naibol'shii vozmozhnyi koefficient szhatiya
pri kodirovanii s ispol'zovaniem togo zhe samogo alfavita. Nazovem raznost' edinicy
i otnositel'noi entropii izbytochnost'yu. Izbytochnost' angliiskogo yazyka,
pri rassmotrenii statisticheskih struktur na masshtabah ne bolee vos'mi bukv,
sostavlyaet poryadka ![]() . Eto znachit, chto: kogda my pishem angliiskii tekst,
polovina ego opredelyaetsya statisticheskoi strukturoi yazyka, a polovina vybiraetsya
nami svobodno. Ocenka
. Eto znachit, chto: kogda my pishem angliiskii tekst,
polovina ego opredelyaetsya statisticheskoi strukturoi yazyka, a polovina vybiraetsya
nami svobodno. Ocenka ![]() poluchaetsya neskol'kimi nezavisimymi
metodami, dayushimi primerno odinakovyi rezul'tat, - raschetom entropii priblizhenii
k angliiskomu yazyku, udaleniem s posleduyushim vosstanovleniem chasti bukv iz
angliiskogo teksta, i tak dalee. Tak, esli tekst mozhet byt' polnost'yu vosstanovlen
posle udaleniya iz nego poloviny bukv, ego izbytochnost' dolzhna byt' bol'she
poluchaetsya neskol'kimi nezavisimymi
metodami, dayushimi primerno odinakovyi rezul'tat, - raschetom entropii priblizhenii
k angliiskomu yazyku, udaleniem s posleduyushim vosstanovleniem chasti bukv iz
angliiskogo teksta, i tak dalee. Tak, esli tekst mozhet byt' polnost'yu vosstanovlen
posle udaleniya iz nego poloviny bukv, ego izbytochnost' dolzhna byt' bol'she ![]() .
Eshe odin metod osnovan na nektorvyh izvestnyh rezul'tatah kriptografii.
.
Eshe odin metod osnovan na nektorvyh izvestnyh rezul'tatah kriptografii.
Dve krainosti izbytochnosti angliiskoi prozy - Osnovnoi Angliiskii (Beisik Inglish, Basic English) i kniga Dzheimsa Dzhoisa ``Pominki po Finneganu''. Slovar' Beisik Inglish ogranichen 850 slovami, i ego izbytochnost' ochen' velika, chto otrazhaetsya v uvedichenii ob'ema soobsheniya pri pereaode ego v dannyi dialekt. Dzhois zhe, naoborot, rasshiryaet leksikon, dostigaya takim obrazom uplotneniya semanticheskogo soderzhaniya.
S izbytochnost'yu yazyka svyazano sushestvovanie zagadok-krossvordov. Pri nulevoi
izbytochnosti lyuboe bukvosochetanie yavlyaetsya priemlemym tekstom, i lyuboi dvumernyi
massiv bukv obrazuet krossvord. Esli zhe izbytochnost' dostatochno velika, yazyk
nalashaem slishkom mnogo ogranichenii, chto delaet nevozmozhnym sushestvovanie bol'shih
krossvordov. Bolee tshatel'nyi analiz pokazyvaet, chto pri sluchainoi
prirode ogranichenii yazyka bol'shie krossvordy vozmozhny lish' pri izbytochnosti
ego poryadka ![]() . Pri izbytochnosti
. Pri izbytochnosti ![]() stanovyatsya
vozmozhnymi trehmernye krossvordy, i tak dalee.
stanovyatsya
vozmozhnymi trehmernye krossvordy, i tak dalee.
Predstavlenie operacii kodirovaniya i dekodirovaniya
My vse eshe ne predstavili matematicheski operacii, proizvodimye peredatchikom
i premnikom pri kodirovanii i dekodirovanii informacii. Nazovem oba etih
pribora ![]() . Preobrazovatel' poluchaet na vhod
nekotoryi nabor vhodnyh simvolov, i vydaet nabor vyhodnyh simvolov. Preobrazovatel'
mozhet imet' vnutrennyuyu pamyat', tak chto informaciya na vyhode budet zaviset' ne tol'ko
ot tekushego postupivshego na vhod simvola, no takzhe i ot vseh predshestvuyushih.
My budet schitat' vnutrennyuyu pamyat' konechnoi, to est' predpolagat' nalichie u preobrazovatelya
konechnogo chisla vnutrennih sostoyanii
. Preobrazovatel' poluchaet na vhod
nekotoryi nabor vhodnyh simvolov, i vydaet nabor vyhodnyh simvolov. Preobrazovatel'
mozhet imet' vnutrennyuyu pamyat', tak chto informaciya na vyhode budet zaviset' ne tol'ko
ot tekushego postupivshego na vhod simvola, no takzhe i ot vseh predshestvuyushih.
My budet schitat' vnutrennyuyu pamyat' konechnoi, to est' predpolagat' nalichie u preobrazovatelya
konechnogo chisla vnutrennih sostoyanii ![]() , takih, chto simvol na vyhode
yavlyaetsya funkciei simvola na vhode i tekushego sostoyaniya. Sleduyushee sostoyanie
yavlyaetsya eshe odnoi funkciei etih dvuh velichin. Takim obrazom, preobrazovatel'
mozhet byt' opisan dvumya funkciyami:
, takih, chto simvol na vyhode
yavlyaetsya funkciei simvola na vhode i tekushego sostoyaniya. Sleduyushee sostoyanie
yavlyaetsya eshe odnoi funkciei etih dvuh velichin. Takim obrazom, preobrazovatel'
mozhet byt' opisan dvumya funkciyami:
gde
| - | | |
| - | sostoyanie preobrazovatelya pri poluchenii
| |
| - | vyhodnoi simvol (ili posledovatel'nost' simvolov),
formiruemyi pri poluchenii simvola |
Esli vyhodnoi simvol odnogo iz preobrazovatelei mozhet byt' podan na vhod drugogo, ih mozhno soedinit' posledovatel'no i poluchit' eshe odin preobrazovatel'. Esli sushestvuet preobrazovatel', preobrazuyushii vyhodnuyu informaciyu pervogo v ego zhe vhodnuyu, pervyi preobrazovatel' nazovem nesingulyarnym, a vtoroi - obratnym k nemu.
Teorema 7: Vyhodnaya posledovatel'nost' preobrazovatelya s konechnym chislom sostoyanii yavlyaetsya posledovatel'nost'yu ot statisticheskogo istochnika s konechnym chislom sostoyanii, s entropiei (v edinicu vremeni), ne bol'shei entropii vhodnoi posledovatel'nosti. Esli preobrazovatel' yavlyaetsya nesingulyarnym, eti entropii ravny.
pust' ![]() opisyvaet sostoyanie istochnika, vydayushego posledovatel'nost'
simvolov
opisyvaet sostoyanie istochnika, vydayushego posledovatel'nost'
simvolov ![]() ,
, ![]() - sostoyanie preobrazovatelya,
dayushego na vyhode bloki simvolov
- sostoyanie preobrazovatelya,
dayushego na vyhode bloki simvolov ![]() . Sistemu mozhno opisat'
pryamym proizvedeniem prostranstv ih sostoyanii, to est' prostranstvom
par
. Sistemu mozhno opisat'
pryamym proizvedeniem prostranstv ih sostoyanii, to est' prostranstvom
par ![]() . Soedinim dve tochki etogo prostranstva
. Soedinim dve tochki etogo prostranstva
![]() i
i ![]() liniei, esli
liniei, esli
![]() mozhet sgenerirovat'
mozhet sgenerirovat' ![]() , perevodyashii
, perevodyashii
![]() v
v ![]() tak, chto eta liniya daet veroyatnost'
takogo
tak, chto eta liniya daet veroyatnost'
takogo ![]() . Pometim takuyu liniyu naborom simvolov
. Pometim takuyu liniyu naborom simvolov ![]() ,
vydannyh preobrazovatelem. Entropiya ego mozhet byt' rasschitana kak vzveshennaya summa
po vsem sostoyaniyam. Esli my vnachale prosummiruem po
,
vydannyh preobrazovatelem. Entropiya ego mozhet byt' rasschitana kak vzveshennaya summa
po vsem sostoyaniyam. Esli my vnachale prosummiruem po ![]() , rezul'tiruyushii
chlen budet ne bol'shim sootvetstvuyushego dlya
, rezul'tiruyushii
chlen budet ne bol'shim sootvetstvuyushego dlya ![]() , tak kak
entropiya ne vozrastaet. Esli preobrazovatel' nesingulyaren, soedinim ego
so vhodom obratnogo emu. Esli
, tak kak
entropiya ne vozrastaet. Esli preobrazovatel' nesingulyaren, soedinim ego
so vhodom obratnogo emu. Esli ![]() ,
, ![]() i
i ![]() -
entropii na vyhode istochnika, pervogo i vtorogo preobrazovatelei sootvetstvenno,
to
-
entropii na vyhode istochnika, pervogo i vtorogo preobrazovatelei sootvetstvenno,
to ![]() i, sledovatel'no,
i, sledovatel'no, ![]() .
.
Pust' my imeem nabor ogranichenii na vozmozhnye posledovatel'nosti, kotorye
mozhno predstvait' v vide lineinogo grafa, podobnogo izobrazhennomu na ris. 2.
Esli veroyatnosti ![]() pripisany vsevozmozhnym liniyam,
soedinyayushim sostoyanie
pripisany vsevozmozhnym liniyam,
soedinyayushim sostoyanie ![]() s sostoyaniem
s sostoyaniem ![]() , eta sistema
stanovitsya istochnikom. Odno iz sopostavlenii maksimiziruet entropiyu na vyhode
(sm. prilozhenie 4).
, eta sistema
stanovitsya istochnikom. Odno iz sopostavlenii maksimiziruet entropiyu na vyhode
(sm. prilozhenie 4).
Teorema 8:
Pust' sistema ogranichenii rassmatrivaetsya kak kanal s propusknoi sposobnost'yu
![]() . Esli my primem
. Esli my primem
gde ![]() - dlitel'nost'
- dlitel'nost' ![]() -togo simvola,
perevodyashego sistemu iz sostoyaniya
-togo simvola,
perevodyashego sistemu iz sostoyaniya ![]() v
v ![]() , i
, i ![]() udovletvoryaet usloviyu
udovletvoryaet usloviyu
to $H$ maksimal'na i ravna $C$.
Nadleashim vyborom veroyatnostei perehoda entropiya simvolov v kanale mozhet byt' dovedena do propusknoi sposobnosti kanala.
Osnovnaya teorema dlya kanala bez shuma
Teper' my obosnuem interpretaciyu ![]() kak tempa generacii informacii,
pokazav, chto
kak tempa generacii informacii,
pokazav, chto ![]() opredelyaet trebuemuyu dlya naibolee effektivnogo
kodirovaniya propusknuyu sposobnost' kanala.
opredelyaet trebuemuyu dlya naibolee effektivnogo
kodirovaniya propusknuyu sposobnost' kanala.
Teorema 9:
Pust' entropiya istochnika est' ![]() (bit na simvol), a propusknaya
sposobnost' kanala -
(bit na simvol), a propusknaya
sposobnost' kanala - ![]() (bit v sekundu). Togda vozmozhno tak
zakodirovat' informaciyu ot istochnika, chto srednii temp ee peredachi po kanalu budet
, gde
(bit v sekundu). Togda vozmozhno tak
zakodirovat' informaciyu ot istochnika, chto srednii temp ee peredachi po kanalu budet
, gde ![]() mozhet byt' sdelana
v proizvol'noi stepeni maloi. Nevozmozhno peredat' informaciyu v tempe, bol'shem
.
mozhet byt' sdelana
v proizvol'noi stepeni maloi. Nevozmozhno peredat' informaciyu v tempe, bol'shem
.
Utverzhdenie teoremy o nevozmozhnosit peredachi s tempom, bol'shim ,
mozhet byt' dokazana s ispol'zovaniem togo, chto entropiya podavaemogo v kanal
za sekundu nabora simvolov ravna entropii istochnika, tak kak preobrazovatel' dolzhen
byt' nesingulyarnym, i, krome togo, eta entropiya ne mozhet byt' bol'she propusknoi
sposobnosti kanala. Sledovatel'no, ![]() , i chislo simvolov
v sekundu
, i chislo simvolov
v sekundu ![]() .
.
Pervaya zhe chast' teoremy dokazyvaetsya dvumya razlichnymi metodami. Pervyi zaklyuchaetsya
v rassmotrenii nabora vseh posledovatel'nostei ![]() simvolov, generiruemyh
istochnikom. Dlya bol'shih
simvolov, generiruemyh
istochnikom. Dlya bol'shih ![]() my mozhem razbit' ih na dve gruppy:
soderzhashuyu posledovatel'nosti koroche
my mozhem razbit' ih na dve gruppy:
soderzhashuyu posledovatel'nosti koroche ![]() simvolov i
soderzhashuyu posledovatel'nosti koroche
simvolov i
soderzhashuyu posledovatel'nosti koroche ![]() (
(![]() zdes' est' logarifm chisla razlichnyh simvolov)
s polnoi veroyatnost'yu men'she
zdes' est' logarifm chisla razlichnyh simvolov)
s polnoi veroyatnost'yu men'she ![]() . S rostom
. S rostom ![]()
![]() i
i ![]() stremyatsya k nulyu. Chislo signalov dlitel'nosti
stremyatsya k nulyu. Chislo signalov dlitel'nosti ![]() v kanale
bol'she
v kanale
bol'she ![]() (gde
(gde ![]() malo) pri
dostatochno bol'shih
malo) pri
dostatochno bol'shih ![]() . Esli my primem
. Esli my primem
to chislo posledovatel'nostei simvolov kanala dlya gruppy bol'shoi veroyatnosti
budet bostatochno bol'shim pri bol'shih ![]() i
i ![]() (i maloi
(i maloi ![]() ),
a krome togo, budet eshe neskol'ko posledovatel'nostei maloi veroyatnosti.
Gruppa vysokoi veroyatnosti kodiruetsya proizvol'nym odnoznachnym sopostavleniem
s elementami etogo mnozhestva. Ostal'nye posledovatel'nosti kodiruyutsya bolee
dlinnymi posledovatel'nostyami, nachinayushimisya i zakanchivayushimisya elementami,
ne ispol'zuemymi dlya kodirovaniya gruppy vysokoi veroyatnosti. Eti elementy
(otdel'nye simvoly ili ih gruppy) signaliziruyut nachalo i konec dlya drugoi
kodirovki. Mezhdu nimi daetsya dostatochnoe vremya dlya peredachi soobshenii
maloi veroyatnosti. Eto trebuet
),
a krome togo, budet eshe neskol'ko posledovatel'nostei maloi veroyatnosti.
Gruppa vysokoi veroyatnosti kodiruetsya proizvol'nym odnoznachnym sopostavleniem
s elementami etogo mnozhestva. Ostal'nye posledovatel'nosti kodiruyutsya bolee
dlinnymi posledovatel'nostyami, nachinayushimisya i zakanchivayushimisya elementami,
ne ispol'zuemymi dlya kodirovaniya gruppy vysokoi veroyatnosti. Eti elementy
(otdel'nye simvoly ili ih gruppy) signaliziruyut nachalo i konec dlya drugoi
kodirovki. Mezhdu nimi daetsya dostatochnoe vremya dlya peredachi soobshenii
maloi veroyatnosti. Eto trebuet
gde ![]() malo. Srednii temp peredachi simvolov soobsheniya v sekundu
togda budet bol'she, chem
malo. Srednii temp peredachi simvolov soobsheniya v sekundu
togda budet bol'she, chem
S rostom ![]()
![]() ,
, ![]() i
i ![]() stremyatsya k nulyu, a temp stremitsya k .
stremyatsya k nulyu, a temp stremitsya k .
Drugim sposobom takogo kodirovaniya (i. sledovatel'no, dokazatel'stva teoremy)
mozhno opisat' sleduyushim obrazom. Otsortiruem soobsheniya dliny ![]() po ubyvaniyu veroyatnosti,
po ubyvaniyu veroyatnosti, ![]() .
Pust' - summarnaya veroyatnost' vplot' do
.
Pust' - summarnaya veroyatnost' vplot' do
![]() (ne vklyuchaya
(ne vklyuchaya ![]() ). Vnachale zakodiruem v dvoichnuyu
sistemu. Dvoichnym kodom dlya soobsheniya
). Vnachale zakodiruem v dvoichnuyu
sistemu. Dvoichnym kodom dlya soobsheniya ![]() budet predstavlenie
budet predstavlenie
![]() dvoichnym chislom. Eto predstavlenie razmeshaetsya na
dvoichnym chislom. Eto predstavlenie razmeshaetsya na ![]() poziciyah, gde
poziciyah, gde ![]() - celoe chislo, udovletvoryayushee usloviyu
- celoe chislo, udovletvoryayushee usloviyu
Takim obrazom, soobsheniya s vysokoi veroyatnost'yu predstavlyayutsya bolee korotkim kodom, chem maloveroyatnye. Iz etih neravenstv poluchaem
Kod dlya ![]() budet otlichat'sya ot vseh posleduyushih v odnom ili
bolee iz sostavlyayushih ego
budet otlichat'sya ot vseh posleduyushih v odnom ili
bolee iz sostavlyayushih ego ![]() simvolov, tak kak vse ostal'nye
simvolov, tak kak vse ostal'nye
![]() kak minimum na
kak minimum na ![]() bol'she, i ih
dvoichnye predstavleniya razlichayutsya v pervyh
bol'she, i ih
dvoichnye predstavleniya razlichayutsya v pervyh ![]() poziciyah.
Sledovatel'no, vse kody razlichny, i vosstanovlenie soobsheniya po ego kodu
vozmozhno. Esli posledovatel'nosti kanala sami po sebe ne yavlyayutsya dvoichnymi,
oni mogut byt' svedeny k nim proizvol'nym obrazom tak, chtoby dvoichnyi kod
odnoznachno preobrazovyvalsya by v signal, priemlemyi dlya kanala.
poziciyah.
Sledovatel'no, vse kody razlichny, i vosstanovlenie soobsheniya po ego kodu
vozmozhno. Esli posledovatel'nosti kanala sami po sebe ne yavlyayutsya dvoichnymi,
oni mogut byt' svedeny k nim proizvol'nym obrazom tak, chtoby dvoichnyi kod
odnoznachno preobrazovyvalsya by v signal, priemlemyi dlya kanala.
Srednee chislo ![]() dvoichnyh cifr na simvol ishodnogo soobsheniya
mozhet byt' legko oceneno. Imeem
dvoichnyh cifr na simvol ishodnogo soobsheniya
mozhet byt' legko oceneno. Imeem
V to zhe vremya
i sledovatel'no
S rostom ![]()
![]() stremitsya k
stremitsya k ![]() , entropii
istochnika, i
, entropii
istochnika, i ![]() stremitsya k
stremitsya k ![]() .
.
Osyuda vidno, chto neeffektivnost' kodirovaniya, to est' ispol'zovanie ne vseh iz ![]() simvolov, mozhet byt' dovedena do
simvolov, mozhet byt' dovedena do ![]() s dobavleniem raznicy
mezhdu istinnoi entropiei
s dobavleniem raznicy
mezhdu istinnoi entropiei ![]() i ee ocenkoi
i ee ocenkoi ![]() po
posledovatel'nostyam dliny
po
posledovatel'nostyam dliny ![]() . Procent vremeni, izbytochnogo
po otnosheniyu k ideal'nomu sluchayu, sootvetstvenno, mozhet byt' sdelan men'shim
. Procent vremeni, izbytochnogo
po otnosheniyu k ideal'nomu sluchayu, sootvetstvenno, mozhet byt' sdelan men'shim
Etot metod kodirovaniya prakticheski sovpadaet s predlozhennym nezavisimo
R. M. Fano (Technical Report No. 65, The Research Laboratory of Electronics, M.I.T., March 17, 1949.),
kotoryi zaklyuchaetsya v sortirovke soobshenii dliny ![]() po ubyvaniyu ih veroyatnosti.
V dal'neishem eti soobsheniya delyatsya na dve gruppy s kak mozhno bolee blizkimi
polnymi veroyatnostyami. Dlya soobshenii pervoi gruppy pervoi dvoichnoi cifroi budet
0, dlya vtoroi - 1. Gruppy takim zhe obrazom delyatsya dalee, vplot' do togo, chto
v kazhdoi gruppe ostaetsya po odnomu soobsheniyu. Legko videt', chto s nebol'shoi
raznicei (v osnovnom v poslednem znake) eto analogichno processu, opisannomu nami
vyshe.
po ubyvaniyu ih veroyatnosti.
V dal'neishem eti soobsheniya delyatsya na dve gruppy s kak mozhno bolee blizkimi
polnymi veroyatnostyami. Dlya soobshenii pervoi gruppy pervoi dvoichnoi cifroi budet
0, dlya vtoroi - 1. Gruppy takim zhe obrazom delyatsya dalee, vplot' do togo, chto
v kazhdoi gruppe ostaetsya po odnomu soobsheniyu. Legko videt', chto s nebol'shoi
raznicei (v osnovnom v poslednem znake) eto analogichno processu, opisannomu nami
vyshe.
Obsuzhdenie i primery
V elektrotehnike dlya polucheniya maksimal'noi peredachi moshnosti ot generatora
k nagruzke generator dolzhen obladat' takimi svoistvami, chtoby s tochki zreniya
nagruzki ego soprotivlenie bylo ravno soprotivleniyu ee. V nashem sluchae situaciya primerno
analogichna. Preobrazovatel', kotoryi zanimaetsya kodirovaniem soobsheniya, dolzhen
sootvetstvovat' istochniku v statisticheskom smysle. Istochnik i preobrazovatel'
s tochki zreniya kanala dolzhny obladat' statisticheskimi svoistvami istochnika,
maksimiziruyushego entropiyu v kanale. Soderzhaniem teoremy 9 yavlyaetsya to, chto,
hotya ideal'noe sootvetstvie v obshem sluchae nevozmozhno, my mozhem priblizhat'sya k nemu
s kakoi ugodno stepen'yu tochnosti. Otnoshenie deistvitel'nogo tempa peredachi
k propusknoi sposobnosti kanala ![]() mozhet byt' nazvano
effektivnost'yu sistemy kodirovaniya. Ona, estestvenno, ravna otnosheniyu
deistvitel'noi entropii simvolov v kanale k maksimal'no vozmozhnomu znacheniyu.
mozhet byt' nazvano
effektivnost'yu sistemy kodirovaniya. Ona, estestvenno, ravna otnosheniyu
deistvitel'noi entropii simvolov v kanale k maksimal'no vozmozhnomu znacheniyu.
V obshem sluchae ideal'noe ili pochti ideal'noe kodirovanie trebuet dlitel'nyh zaderzhek i peredatchike i priemnike. V rassmatrivaemom sluchae otsutstviya shuma glavnoi funkciei etih zaderzhek yavlyaetsya dostatochno tshatel'noe sopostavlenie veroyatnostei posledovatel'nostei sootvetstvuyushih dlin. Pri horoshem kodirovanii logarifm sovmestnoi veroyatnosti dlinnogo soobsheniya dolzhen byt' proporcionalen dlitel'nosti sootvetstvuyushego signala, tochnee
dolzhno byt' malo prakticheski dlya vseh dlinnyh soobshenii.
Esli istochnik generiruet tol'ko odno fiksirovannoe soobshenie, ego entropiya
ravna nulyu, i kanal ne trebuetsya. K primeru, vychislitel'naya mashina dlya rascheta
posledovatel'nyh cifr chisla ![]() vydaet determinirovannuyu
posledovatel'nost' bez sluchainoi sostavlyayushei. Dlya peredachi takogo signala net
nuzhdy v kanale - dostatochno postroit' vtoruyu analogichnuyu mashinu. Odnako, inogda
eto nepraktichno. V takom sluchae my mozhem prenebrech' nekotoroi informaciei
o strukture signala. Mozhno rassmatrivat' cifry chisla
vydaet determinirovannuyu
posledovatel'nost' bez sluchainoi sostavlyayushei. Dlya peredachi takogo signala net
nuzhdy v kanale - dostatochno postroit' vtoruyu analogichnuyu mashinu. Odnako, inogda
eto nepraktichno. V takom sluchae my mozhem prenebrech' nekotoroi informaciei
o strukture signala. Mozhno rassmatrivat' cifry chisla ![]() kak
sluchainuyu posledovatel'nost' i razrabotat' sistemu dlya peredachi proizvol'noi
cifrovoi informacii. Analogichno my mogli by vospol'zovat'sya lish' chast'yu nashego
znaniya statisticheskoi struktury angliiskogo yazyka. Dlya takogo sluchaya mozhno rassmotret'
istochnik s maksimal'noi entropiei, udovletvoryayushii vybrannym nami statisticheskim
usloviyam. Entropiya takogo istochnika opredelyaet propusknuyu sposobnost' kanala,
kotoraya yavlyaetsya neobhodimoi i dostatochnoi. Tak, v sluchae peredachi chisla
kak
sluchainuyu posledovatel'nost' i razrabotat' sistemu dlya peredachi proizvol'noi
cifrovoi informacii. Analogichno my mogli by vospol'zovat'sya lish' chast'yu nashego
znaniya statisticheskoi struktury angliiskogo yazyka. Dlya takogo sluchaya mozhno rassmotret'
istochnik s maksimal'noi entropiei, udovletvoryayushii vybrannym nami statisticheskim
usloviyam. Entropiya takogo istochnika opredelyaet propusknuyu sposobnost' kanala,
kotoraya yavlyaetsya neobhodimoi i dostatochnoi. Tak, v sluchae peredachi chisla ![]() edinstvennym statisticheskim usloviem yavlyaetsya to, chto vse simvoly vybirayutsya iz
nabora
edinstvennym statisticheskim usloviem yavlyaetsya to, chto vse simvoly vybirayutsya iz
nabora ![]() ; dlya angliiskogo teksta my mozhem ostavit'
lish' trebovanie sootvetstviya chastot bukv. Togda istochnik s maksimal'noi
entropiei yavlyaetsya pervym priblizheniem k angliiskomu yazyku, i ego entropiya
opredelyaet trebuemuyu propusknuyu sposobnost' kanala.
; dlya angliiskogo teksta my mozhem ostavit'
lish' trebovanie sootvetstviya chastot bukv. Togda istochnik s maksimal'noi
entropiei yavlyaetsya pervym priblizheniem k angliiskomu yazyku, i ego entropiya
opredelyaet trebuemuyu propusknuyu sposobnost' kanala.
V kachestve prostogo primera vysheizlozhennyh rezul'tatov rassmotrim istochnik,
generiruyushii posledovatel'nost' nezavisimyh bukv, vybrannyh iz A, B, C, D
s veroyatnostyami ![]() ,
, ![]() ,
, ![]() ,
, ![]() sootvetstvenno. Togda
sootvetstvenno. Togda
Sledovatel'no, dlya takogo istochnika mozhno razrabotat' sistemu predstavleniya
soobshenii dvoichnym kodom so stepen'yu szhatiya vplot' do ![]() dvoichnyh
cifr na simvol. V dannom primere eto predel'noe znachenie mozhet byt' dostignuto
pri ispol'zovanii sleduyushego koda (poluchennogo metodom, ispol'zovannym vo
vtorom variante dokazatel'stva teoremy 9):
dvoichnyh
cifr na simvol. V dannom primere eto predel'noe znachenie mozhet byt' dostignuto
pri ispol'zovanii sleduyushego koda (poluchennogo metodom, ispol'zovannym vo
vtorom variante dokazatel'stva teoremy 9):
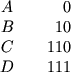
Srednee chislo dvoichnyh znakov, ispol'zovannyh dlya kodirovaniya posledovatel'nosti
dlinoi ![]() simvolov budet
simvolov budet
Legko videt', chto dvoichnye znaki 0 i 1 imeyut veroyatnosti ![]() kazhdyi,
sledovatel'no,
kazhdyi,
sledovatel'no, ![]() dlya zakodirovannoi posledovatel'nosti ravno
odnomu bitu na simvol. Tak kak v srednem my imeem
dlya zakodirovannoi posledovatel'nosti ravno
odnomu bitu na simvol. Tak kak v srednem my imeem ![]() dvoichnyh
znakov na ishodnyi simvol, entropiya v edinicu vremeni ostaetsya neizmennoi.
Naibol'shei vozmozhnoi entropiei ishodnogo nabora budet
dvoichnyh
znakov na ishodnyi simvol, entropiya v edinicu vremeni ostaetsya neizmennoi.
Naibol'shei vozmozhnoi entropiei ishodnogo nabora budet ![]() ,
dostigaemaya pri veroyatnostyah bukv
,
dostigaemaya pri veroyatnostyah bukv ![]() ,
, ![]() ,
, ![]() ,
, ![]() , ravnyh
$\frac14$ kazhdaya. Takim obrazom, otnositel'naya entropiya ravna
, ravnyh
$\frac14$ kazhdaya. Takim obrazom, otnositel'naya entropiya ravna ![]() Dvoichnaya posledovatel'nost' mozhet byt' otobrazhena na mnozhestvo
ishodnyh simvolov pri pomoshi sleduyushei tablicy:
Dvoichnaya posledovatel'nost' mozhet byt' otobrazhena na mnozhestvo
ishodnyh simvolov pri pomoshi sleduyushei tablicy:

Takoe dvoinoe preobrazovanie kodiruet ishodnoe soobshenie temi zhe simvolami,
no s koefficientom szhatiya ![]() .
.
V kachestve eshe odnogo primera rassmotrim istochnik, vydayushii bukvy A i B
s veroyatnostyami ![]() dlya A i
dlya A i ![]() dlya B.
Pri
dlya B.
Pri ![]()
V takoi situacii mozhno postroit' dostatochno horoshuyu sistemu kodirovaniya soobshenii
v dvoichnom kanale, posylaya nekotoruyu specil'nuyu posledovatel'nost', skazhem,
0000, dlya maloveroyatnogo simvola A, i zatem chislo, harakterizuyushee
kolichestvo sleduyushih za nim simvolov B. Eto kolichestvo mozhet byt'
oharakterizovano dvoichnym predstavleniem pri udalenii vseh chisel, soderzhashih
special'nuyu posledovatel'nost'. V nashem sluchae vse chisla vplot' do 16 predstavlyayutsya
kak obychno, 16 predstavlyaetsya sleduyushim chislom, ne soderzhashim special'noi posledovatel'nosti,
a imenno ![]() , i tak dalee.
, i tak dalee.
Mozhno pokazat', chto pri ![]() sistema kodirovaniya stremitsya k
ideal'noi pri nadlezhashem vybore special'noi posledovatel'nosti.
sistema kodirovaniya stremitsya k
ideal'noi pri nadlezhashem vybore special'noi posledovatel'nosti.
<< Vvedenie | Oglavlenie | Chast' 2. Diskretnyi zashumlennyi kanal >>
|
Publikacii s klyuchevymi slovami:
matematika - informaciya - Shennon
Publikacii so slovami: matematika - informaciya - Shennon | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |