Astronet > Matematicheskaya teoriya svyazi. Chast' 2. Diskretnyi zashumlennyi kanal

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Klod Shennon: Matematicheskaya teoriya svyazi

<< Chast' 1. Diskretnye sistemy bez shuma | Oglavlenie | Chast' 3. Matematicheskie osnovy >>

Chast' 2. Diskretnyi zashumlennyi kanal

Predstavlenie zashumlennogo diskretnogo kanala

Rassmotrim teper' situaciyu, pri kotoroi signal podvergaetsya vozdeistviyu shuma libo v processe peredachi, libo na odnom iz koncov kanala. Eto znachit, chto prinyatyi signal ne obyazatel'no sovpadaet s tem, kotoryi byl otpravlen peredatchikom. Mozhno vydelit' dva razlichnyh klassa takih situacii. Esli odin i tot zhe peredavaemyi signal vsegda privodit k odinakovomu signalu v priemnike, to est' esli prinyatyi signal yavlyaetsya odnoznachnoi funkciei peredannogo, mozhno skazat', chto imeet mesto iskazhenie signala. Esli eta funkciya imeet obratnuyu, to est' kazhdyi signal na v priemnike vyzyvaetsya lish' odnim signalom v peredatchike, eto iskazhenie mozhet byt' uchteno, po krainei mere v principe, primeneniem sootvetstvuyushei korrektiruyushei operacii k prinyatomu signalu.

Vtoroi, bolee interesnyi klass, sostavlyayut situacii, v kotoryh peredavaemyi signal preterpevaet ne vsegda odinakovye izmeneniya. V takom sluchae my mozhem schitat' prinyatyi signal $E$ funkciei kak peredannogo $S$ , tak i shuma $N$ .

$E = f(S,N)$

Shum yavlyaetsya sluchainoi velichinoi, tochno takoi zhe, kak i rassmotrennoe vyshe soobshenie. V obshem sluchae on mozhet byt' opisan sootvetstvuyushim stohasticheskim processom. Naibolee obshim sluchaem zashumlennogo kanala, kotoryi my rassmotrim, yavlyaetsya obobshenie opisannogo vyshe besshumovogo kanala s konechnym chislom sostoyanii. Predpolozhim, chto est' konechnoe chislo sostoyanii i nabor veroyatnostei

$p_{\alpha,i}(\beta,j).$

Eto veroyatnost' togo, chto, esli kanal nahoditsya v sostoyanii $\alpha$ i peredaetsya simvol $i$ , na vyhode budet prinyat simvol $j$ i kanal pereidet v sostoyanie $\beta$ . Zdes' $\alpha$ i $\beta$ probegayut po vsem vozmozhnym sostoyaniyam, $i$ - po vsem vozmozhnym peredavaemym simvolam, i $j$ - po vsem vozmozhnym prinimaemym. V sluchae nezavisimogo iskazheniya posledovatel'nyhz simvolov sostoyanie tol'ko odno, i kanal opisyvaets naborom veroyatnostei $p_i(j)$ prinyat' simvol $j$ pri peredache $i$ .

Esli v kanal podayutsya simvoly s istochnika, rabotayut dva sluchainyh processa: istochnik i shum. Sootvetstvenno, mozhno vychislit' neskol'ko razlichnyh entropii. Eto entropiya $H(x)$ istochnika (ili entropiya na vhode v kanal, chto ekvivalentno predydushemu dlya nesingulyarnogo preobrazovatelya), entropiya na vyhode iz kanala, to est' prinyatogo signala, kotoruyu my budem oboznachat' $H(y)$ . Pri otsustvii shuma $H(y) = H(x)$ . Sovmestnuyu entropiyu na vhode i vyhode oboznachim $H(xy)$ . Nakonec, mozhno opredelit' dve uslovnyh entropii $H_x(y)$ i $H_y(x)$ , entropii signala na vyhode v sluchae, esli izvesten signal na vhode, i naoborot. Eto velichiny svyazany sootnosheniem

$H(x,y) = H(x) + H_x(y) = H(y) + H_y(x).$

Kazhduyu iz etih entropii mozhno opredelit' v raschete kak na odnu sekundu, tak i na odin simvol.

Oshibochnost' i propusknaya sposobnost' kanala

Esli kanal yavlyaetsya zashumlennym, v obshem sluchae nevozmozhno s uverennost'yu vosstanovit' ishodnoe soobshenie ili peredannyi signal nikakim preobrazovaniem prinyatogo signala $E$ . Odnako, sushestvuyut metody peredachi informacii, optimal'nye dlya bor''y s shumami. Rassmotrim etu zadachu.

Pust' est' dva vozmozhnyh simvola, 0 i 1, peredavaemyh s tempom 1000 simvolov v sekundu s veroyatnostyami $p_0 = p_1 = \frac12$ . Takim obrazom, istochnik vydaet informaciyu s tempom 1000 bit v sekundu. Pri peredache nalichie shuma privodit k oshibkam, tak chto v srednem 1 iz 100 simvolov prinimaetsya nepravil'no (0 vmesto 1, ili zhe 1 vmesto 0). Kakov temp peredachi informacii? Yasno, chto on menbshe 1000 bit v sekundu, tak kak primerno $1\%$ simvolov prinimaetsya nepravil'no. Pervym pobuzhdeniem budet skazat', chto temp peredachi raven 990 bit v sekundu (polucheno prostym vychitaniem kolichestva nepravil'no prinyatyh simvolov), odnako etot otvet neudovletvoritelen, tak kak ne uchityvaet togo fakta, chto priemnik ne znaet, kakie imenno simvoly prinyaty neverno. Eto stanovitsya ochevidnym iz rassmotreniya predel'nogo sluchaya, pri kotorom prinimaemyi signal sovershenno ne zavisit ot peredavaemogo. V takom sluchae veroyatnost' poluchit' 1 ravna $\frac12$ , i primerno polovina prinyatyh simvolov sluchaino okazyvaetsya vernoi. Po vysheprivedennomu opredeleniyu okazyvaetsya, chto temp peredachi informacii raven 500 bit v sekundu, hotya ochevidno, chto informaciya ne peredaetsya sovsem. Nastol'ko zhe ``horoshuyu'' peredachu my by poluchili, sovsem otklyuchiv kanal i brosaya monetu v tochke priema.

Ochevidno, chto korrektnoi popravkoi k kolichestvu peredavaemoi informacii budet kolichestvo informacii, otsutstvuyushee v prinyatom signale, ili zhe neopredelennost' peredannogo signala pri izvestnom prinyatom. Vspominaya predshestvuyushee obsuzhdenie entropii kak mery neopredelennosti, razumno vospol'zovat'sya uslovnoi entropiei soobsheniya. Znaya prinyatyi signal, my poluchaem meru etoi utrachennoi informaciei. Eto deistvitel'no korrektnoe opredelenie, kak budet pokazano dalee. Takim obrazom, temp deistvitel'noi peredachi $R$ mozhet byt' poluchen vychitaniem iz tempa vydachi informacii istochnikom vrednego tempa uslovnoi entropii.

$R = H(x) - H_y(x)$

Nazovem dlya udobstva uslovnuyu entropiyu $H_y(x)$ oshibochnost'yu. Ona harakterizuet srednyuyu neopredelennost' prinyatogo signala.

V vysheprivedennom primere, esli prinyat nol', aposteriornaya veroyatnost' togo, chto byl peredan nol', ravna 0.99, togda kak togo, chto byla peredana edinica - 0.01. Sledovatel'no

ili 81 bit v sekundu. Mozhno skazat', chto temp peredachi informacii raven $1000 - 81 = 919$ . V predel'nom sluchae, kogda peredannyi nol' s ravnoi veroyatnost'yu prinimaetsya i kak nol', kak edinica, aposteriornye veroyatnosti ravny $\frac12$ , i

ili 1000 bit v sekundu. Temp peredachi raven nulyu, kak i dolzhno byt'.

Nizhesleduyushaya teorema daet pryamuyu naglyadnuyu interpretaciyu oshibochnost'yu, pokazyvaya, krome togo, chto eto edinstvennaya podhodyashaya mera. Rassmotrim sistemu svyazi i nablyudatelya (ili vspomogatel'noe ustroistvo), sposobnogo videt' odnovremenno i peredavaemuyu, i vosstanovlennuyu po prinimaemomu signalu informaciyu, soderzhashuyu oshibki iz-za shuma. Nablyudatel' zamechaet eti oshibki i soobshaet o nih priemniku po ``korrektiruyushemu kanalu'', pozvolyaya ih ispravit'. Situaciya shematicheski izobrazhena na risunke 8.

Ris.8. Shematicheskoe izobrazhenie korrektiruyushei sistemy.

Teorema 10: Esli propusknaya sposobnost' korrektiruyushego kanala $H_y(x)$ , mozhno zakodirovat' korrektiruyushuyu informaciyu takim obrazom, chto ee mozhno poslat' po etomu kanalu i skorrektirovat' vse oshibki za isklyucheniem ih proizvol'no maloi doli $\epsilon$ . Eto nevozmozhno, esli propusknaya sposobnost' korrektiruyushego kanala men'she $H_y(x)$ .

Grubo govorya, $H_y(x)$ - kolichestvo dopolnitel'noi informacii, neobhodimoi priemniku dlya korrekcii prinyatogo soobsheniya.

Dlya dokazatel'stva pervoi chasti rassmotrim dlinnye posledovatel'nosti prinyatogo soobsheniya $M'$ i ishodnogo soobsheniya $M$ . Est' logarifmicheski bol'shoe chislo $T H_y(x)$ soobshenii $M$ , kotorye mogli by privesti k prinyatomu soobsheniyu $M'$ . Takim obrazom, neobhodimo peredavat' $T H_y(x)$ dvoichnyh cifr kazhdye $T$ sekund. Eto mozhet byt' sdelano pri chastote oshibok $\epsilon$ v kanale s propusknoi sposobnost'yu $H_y(x)$ .

Vtoroe utverzhdenie mozhet byt' dokazano, esli Dlya dokazatel'stva vtorogo utverzhdeniya zametim, chto dlya lyubyh diskretnyh sluchainyh velichin $x$ , $y$ , $z$

$H_y(x,z) \ge H_y(x).$

Levuyu chast' mozhno preobrazovat'

$H_y(z) + H_{yz}(x) \ge H_y(x)$
$H_{yz}(x) \ge H_y(x) - H_y(z) \ge H_y(x) - H(z).$

Esli my otozhdestvim $x$ s informaciei, vydavaemoi istochnikom, $y$ - s prinyatym signalom, i $z$ - signalom, peredavaemym po korrektiruyushemu kanalu, to pravaya chast' yavlyaetsya raznost'yu oshibochnosti i tempa peredachi po korrektiruyushemu kanalu. Esli etot temp men'she oshibochnosti, to pravaya chast' budet bol'she nulya, i $H_{yz}(x)>0$ . A eta velichina harakterizuet neopredelennost' soobsheniya pri izvestnyh prinyatom i korrektiruyushem signalah. Kogda ona bol'she nulya, chastota oshibok ne mozhet byt' sdelana proizvol'no maloi.

Primer:

Rassmotrim sluchainye oshibki v posledovatel'nosti dvoichnyh cifr, s veroyatnost'yu $p$ togo, chto cifra neverna, i $q=1-p$ - chto verna. Eti oshibki mogut byt' skorrektirovany, esli izvestny ih polozheniya, potomu korrektiruyushii kanal dolzhen peredavat' lish' ih polozheniya. Eto ravnosil'no peredache dvoichnyh znakov s veroyatnostyami $p$ dlya 1 (nevernaya cifra), i $q$ - dlya 0 (vernaya cifra). Dlya etogo trebuetsya kanal s propusknoi sposobnost'yu

$- [p \log p + q \log q ]$

chto ravno oshibochnosti ishodnoi sistemy.

Temp peredachi mozhno zapisat' v dvuh drugih formah, ispol'zuya vysheprivedennye tozhdestva. Imeem

Zdes' pervaya zapis' uzhe byla istolkovana kak raznost' poslannogo kolichestva informacii i ee neopredelennosti; vtoraya harakterizuet raznost' prinyatoi informacii i ee chasti, obuslovlennoi shumom; tret'ya zhe - raznost' summy obeih informacii i sovmestnoi entropii, to est' - chislo bit v sekundu, obshih dlya obeih. Takim obrazom, vse eti vyrazheniya imeyut opredelennoe naglyadnoe istolkovanie.

Propusknaya sposobnost' zashumlennogo kanala dolzhna byt' maksimal'no vozmozhnym tempom peredachi, to est' tempom, pri kotorom istochnik sootvetstvuet kanalu. Opredelim togda propusknuyu sposobnost' kak

$C= \max \bigl(H(x) - H_y(x)\bigr)$

gde maksimum vychislyaetsya po otnosheniyu ko vsem vozmozhnym istochnikam informacii dlya kanala. Dlya besshumovogo kanala $H_y(x) = 0$ , i eto opredelenie svoditsya k dannomu ranee dlya takogo kanala, tak kak ego entropiya ravna ego propusknoi sposobnosti.

Osnovnaya teorema dlya diskretnogo kanala s shumom

Mozhet pokazat'sya udivitel'nym to, chto my vvodim opredelennuyu propusknuyu sposobnost' dlya zashumlennogo kanala, togda kak nadezhnaya peredacha informacii nevozmozhna. Yasno, odnako, chto vvedeniem nekotoroi izbytochnosti v peredavaemuyu informaciyu veroyatnost' oshibki mozhet byt' umen'shena. K primeru, pri mnogokratnoi peredache soobsheniya i posleduyushem statisticheskom analize prinyatoi informacii veroyatnost' oshibki mozhet byt' sdelana ochen' maloi. Mozhno bylo by, odnako, reshit', chto dlya svedeniya etoi veroyatnosti k nulyu izbytochnost' informacii dolzhna vozrastat' beskonechno, chto privelo by k padeniyu tempa peredachi do nulya. Odnako eto neverno. Esli by eto bylo tak, ne moglo by byt' odnoznachno opredelennoi propusknoi sposobnosti kanala - byla by lish' propusknaya sposobnost' pri zadannoi chastote oshibok, ili zhe pri zadannoi oshibochnosti; eta propusknaya sposobnost' stremilas' by k nulyu pri usilenii ogranichenii na oshibki. Na samom zhe dele opredelennaya vyshe propusknaya sposobnost' $C$ imeet vpolne opredelennyi smysl. Mozhno peredat' po kanalu informaciyu s tempom $C$ s proizvol'no maloi chastotoi oshibok ili zhe oshibochnost'yu putem sootvetstvuyushego kodirovaniya. Pri popytke zhe peredachi s bol'shim tempom $C+R_1$ neizbezhno budet nekotoraya oshibochnost', ravnaya ili bol'shaya $R_1$. Priroda ustroena tak, chto my ne smozhem peredat' informaciyu s tempom, bol'shim $C$.

Dannaya situaciya illyustriruetsya ris. 9. Temp postupleniya informacii v kanal otlozhen po gorizontal'noi osi, a oshibochnost' - po vertikal'noi. Vse tochki vyshe zhirnoi linii v zashtrihovannoi oblasti dostizhimy, vse tochki nizhe - nedostizhimy. Tochki na linii v obshem sluchae nedostizhimy, za isklyucheniem dvuh, kotorye obychno mogut byt' dostignuty.

Eti rezul'taty yavlyayutsya opravdaniem vysheprivedennogo opredeleniya $C$, i seichas my ih dokazhem.

Teorema 11: Pust' diskretnyi kanal imeet propusknuyu sposobnost' $C$, a istochnik - entropiyu v sekundu $H$ . Pri $H \le C$ sushestvuet takaya sistema kodirovaniya, chto informaciya ot istochnika mozhet byt' peredana po kanalu s proizvol'no maloi veroyatnost'yu oshibki. Pri $H>C$ vozmozhno tak zakodirovat' informaciyu, chto oshibochnost' budet men'she $H-C+\epsilon$ , gde $\epsilon$ proizvol'no malo. Ne sushestvuet sposoba kodirovaniya, dayushego oshibochnost' men'she $H-C$ .

Sposob dokazatel'stva pervoi chasti sostoit ne v yavnom postroenii trebuemogo sposoba kodirovaniya, a v demonstracii togo, chto takoi sposob dolzhen sushestvovat' v nekotorom mnozhestve sistem kodirovaniya.

Ris.9.Dopustimaya oshibochnost' dlya zadannoi entropii na vhode v kanal.

Na samom dele my provedem usrednenie chastoty oshibok po etomu mnozhestvu i pokazhem, chto eto srednee mozhet byt' sdelano men'shim $\epsilon$ . Esli srednee po nekotoromu naboru chisel men'she $\epsilon$ , dolzhno byt' hotya by odno chislo iz etogo nabora, men'shee $\epsilon$ , chto i posluzhit iskomym dokazatel'stvom.

Propusknaya sposobnost' $C$ zashumlennogo kanala byla opredelena kak

$C= \max\bigl(H(x) - H_y(x)\bigr)$

gde $x$ - vhodnaya informaciya i $y$ - vyhodnaya. Maksimizaciya provoditsya po vsem vozmozhnym istochnikam informacii dlya kanala.

Pust' $S_0$ - istochnik, dlya kotorogo dostigaetsya maksimal'naya propusknaya sposobnost' $C$ . Esli zhe etot temp ne dostigaetsya ni odnim istochnikom, opredelim $S_0$ kak istochnik, dayushii maksimal'nyi temp peredachi. Pust' etot istochnik podaet informaciyu v kanal. Rassmotrim vozmozhnye peredannye i prinyatye posledovatel'nosti dostatochnoi dliny $T$ . Togda spravedlivo sleduyushee:

1. Peredavaemye posledovatel'nosti mozhno razdelit' na dva klassa - soobsheniya s vysokoi veroyatnost'yu, obshim chislom poryadka $2^{T H(x)}$ , i ostal'nye s maloi summarnoi veroyatnost'yu.

2.Analogichno i prinyatye posledovatel'nosti mozhno razdelit' na takie zhe klassy.

3. Kazhdaya vysokoveroyatnaya prinyataya posledovatel'nost' mozhet vyzyvat'sya primerno $2^{T H_y(x)}$ razlichnymi peredannymi. Veroyatnost' togo, chto ona vyzyvaetsya ostal'nymi, mala.

Vse $\epsilon$ i $\delta$ stremyatsya k nulyu s rostom $T$ i priblizheniem $S_0$ k istochniku, maksimiziruyushemu temp peredachi.

Eta situaciya izobrazhena na ris. 10, gde peredavaemye posledovatel'nosti predstavleny tochkami sleva, a prinyatye - sprava. Nabor linii otrazhaet mnozhestvo vozmozhnyh peredannyh posledovatel'nostei dlya dannoi prinyatoi.

Ris.10. Shematicheskoe izobrazhenie svyazi vhodnoi i vyhodnoi informacii v kanale.

Pust' teper' my imeem istochnik s tempom $R$ takim, chto

Obsuzhdenie

Primer diskretnogo kanala i ego propusknaya sposobnost'

Propusknaya sposobnost' kanala v nekotoryh special'nyh sluchayah

Primer effektivnogo kodirovaniya

Prilozhenie 1. Rost chisla blokov simvolov pri uslovii konechnosti chisla sostoyanii

Prilozhenie 2. Poluchenie vyrazheniya 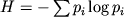$H=-\sum p_i\log p_i$

Prilozhenie 3. Teoremy ob ergodichesih istochnikah

Prilozhenie 4. Maksimizaciya tempa dlya sistemy s ogranicheniyami

Publikacii s klyuchevymi slovami: matematika - informaciya - Shennon Publikacii so slovami: matematika - informaciya - Shennon
Sm. takzhe: Golograficheskii princip i chainik Golograficheskii princip Informaciya Matematika trehmernyh mnogoobrazii Klod Shennon: Biografiya D'Alambera uravnenie D'Alambera operator Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce