Klod Shennon: Matematicheskaya teoriya svyazi
<< Chast' 2. Diskretnyi zashumlennyi kanal | Oglavlenie | Chast' 4. Nepreryvnyi kanal >>
Chast' 3. Matematicheskie osnovy
V dal'neishem my rassmotrim situacii, v kotoryh signaly i/ili soobsheniya yavlyayutsya nepreryvnymi velichinami, v protivopolozhnost' rassmotrennomu ranee diskretnomu sluchayu. Nepreryvnyi sluchai mozhet byt' poluchen predel'nym perehodom iz diskretnogo - deleniem nepreryvnogo mnozhestva soobshenii i signalov na bol'shoe no konechnoe chislo malyh oblastei i vychisleniem velichin po takoi diskretnoi sisteme. S umen'sheniem razmerov otdel'nyh oblastei eti parametry v obshem sluchae stremyatsya k sootvetstvuyushim velichinam nepreryvnoi zadachi. Odnako, poyavlyayutsya i nekotorye novye effekty, krome togo, akcenty smeshayutsya v napravlenii specializacii obshiz rezul'tatov dlya konkretnyh zadach.
V nepreryvnom sluchae my ne budem pytat'sya poluchat' rezul'taty s kak mozhno bol'shei obshnost'yu ili matematicheskoi strogost'yu, tak kak eto potrebovalo by sushestvennogo uglubleniya v abstraktnuyu teoriyu mery i uvelo nas daleko ot osnovnoi linii nashego issledovaniya. Predvaritel'noe rassmotrenie, odnako, pokazyvaet, chto teoriya mozhet byt' sformulirovana polnost'yu aksiomaticheski i strogo tak, chto budet vklyuchat' v sebya kak nepreryvnyi, tak i diskretnyi sluchai, i mnogoe drugoe. Opredelennoye vol'nosti v predel'nyh perehodah v nashei rassmotrenii mogut byt' strogo obosnovany dlya vseh prakticheski interesnyh situacii.
Mnozhestva i ansambli funkcii
Pri rassmotrenii nepreryvnogo sluchaya my budem imet' delo s mnozhestvami i ansamblyami funkcii. Mnozhestvo funkcii, kak sleduet iz nazvaniya, est' prosto nabor ili gruppa ih, zavisyashih obychno ot odnoi peremennoi, vremeni. Ono opredelyaetsya yavnym zadaniem razlichnyh sostavlyayushih ego funkcii, ili zhe svoistvom, kotorym obladayut eto funkcii, a vse ostal'nye - net. Privedem neskol'ko primerov.
-
Mnozhestvo funkcii
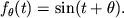
Kazhdoe znachenie
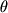 opredelyaet nekotoruyu funkciyu etogo
mnozhestva.
opredelyaet nekotoruyu funkciyu etogo
mnozhestva.
-
Mnozhestvo vseh funkcii, zavivyashih ot vremeni i ne soderzhashih garmonik s
chastotami, bol'shimi
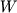 .
.
-
Mnozhestvo vseh funkcii, ogranichennyh chastotnym diapazonom
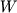 i
amplitudoi
i
amplitudoi 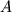 .
.
- Mnozhestvo vseh signalov angliiskoi rechi kak funkcii ot vremeni.
Nazovem ansamblem funkcii mnozhestvo ih s meroi, posredstvom kotoroi mozhno opredelit' veroyatnost' funkcii iz etogo mnozhestva, imeyushei zadannye svoistva. (Matematicheskim yazykom - funkcii prinadlezhat prostranstvu s meroi, prichem ego polnaya mera ravna edinice.). K primeru, dlya mnozhestva
my mozhem zadat' raspredelenie veroyatnosti dlya ![]() ,
, ![]() .
Mnozhestvo pri etom stanovitsya ansamblem.
.
Mnozhestvo pri etom stanovitsya ansamblem.
Privedem eshe neskol'ko primerov ansamblei.
-
Konechnyi nabor funkcii
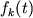 (
(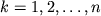 ) s
veroyatnost'yu
) s
veroyatnost'yu 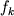 , ravnoi
, ravnoi 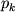 .
.
-
Konechnomernoe semeistvo funkcii
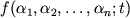
s plotnost'yu veroyatnosti parametrov
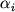
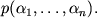
K primeru, mozhno rassmotret' ansambl', opredelyaemyi
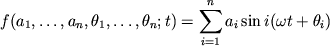
s amplitudami
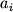 , raspredelennym normal'no i nezavisimo, i fazami
, raspredelennym normal'no i nezavisimo, i fazami
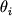 , raspredelennymi ravnomerno (ot
, raspredelennymi ravnomerno (ot 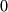 do
do 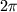 )
i nezavisimo.
)
i nezavisimo.
-
Ansambl'
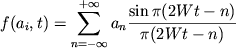
s
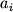 , normal'no raspredelennymi i nezavisimymi s odinakovym
standartnym otkloneniem
, normal'no raspredelennymi i nezavisimymi s odinakovym
standartnym otkloneniem 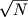 . Eto predstavlenie ``belogo''
shuma, ogranichennogo diapazonom chastot ot
. Eto predstavlenie ``belogo''
shuma, ogranichennogo diapazonom chastot ot 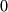 do
do 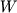 i so srednei moshnost'yu
i so srednei moshnost'yu 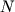 (Eto predstavlenie mozhno schitat' opredeleniem ogranichennogo po chastote
belogo shuma. Ono imeet nekotorye preimushestva pered drugimi ispol'zuemymi,
tak kak soderzhit men'shee chislo predel'nyh perehodov. Vozmozhno, nazvanie
``belyi shum'', shiroko zakrepivsheesya v literature, ne vpolne udachno, tak kak
v optike belym cvetom nazyvayut libo lyuboi nepreryvnyi spektr (v otlichie ot tochechnogo),
libo zhe spektr, ploskii po dlinam voln, a eto ne to zhe samoe, chto ploskii po
chastote spektr.).
(Eto predstavlenie mozhno schitat' opredeleniem ogranichennogo po chastote
belogo shuma. Ono imeet nekotorye preimushestva pered drugimi ispol'zuemymi,
tak kak soderzhit men'shee chislo predel'nyh perehodov. Vozmozhno, nazvanie
``belyi shum'', shiroko zakrepivsheesya v literature, ne vpolne udachno, tak kak
v optike belym cvetom nazyvayut libo lyuboi nepreryvnyi spektr (v otlichie ot tochechnogo),
libo zhe spektr, ploskii po dlinam voln, a eto ne to zhe samoe, chto ploskii po
chastote spektr.).
-
Pust' tochki raspredeleny na osi
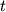 soglasno raspredeleniyu Puassona.
V kazhdoi vybrannoi tochke pomeshaetsya funkciya
soglasno raspredeleniyu Puassona.
V kazhdoi vybrannoi tochke pomeshaetsya funkciya 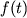 , i eti funkcii
zatem skladyvayutsya, obrazuya ansambl'
, i eti funkcii
zatem skladyvayutsya, obrazuya ansambl'
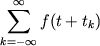
gde
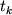 - tochki puassonovskogo raspredeleniya. Etot ansambl' mozhno
schitat' chastnym sluchaem impul'snogo ili drobovogo shuma, v kotorom vse impul'sy
odinakovy.
- tochki puassonovskogo raspredeleniya. Etot ansambl' mozhno
schitat' chastnym sluchaem impul'snogo ili drobovogo shuma, v kotorom vse impul'sy
odinakovy.
- Nabor funkcii angliiskoi rechi, dlya kotorogo za veroyatnosti prinyaty chastoty vstrechaemosti v yazyke.
Nazovem ansambl' funkcii ![]() stacionarnym, esli
rezul'taty rascheta po nemu ne menyayutsya pri proizvol'nom (fiksirovannom)
sdvige po vremeni. Ansambl'
stacionarnym, esli
rezul'taty rascheta po nemu ne menyayutsya pri proizvol'nom (fiksirovannom)
sdvige po vremeni. Ansambl'
stacionaren, esli ![]() raspredelena ravnomerno na intervale ot
raspredelena ravnomerno na intervale ot
![]() do
do ![]() . Pri sdvige kazhdoi iz funkcii na
. Pri sdvige kazhdoi iz funkcii na ![]() poluchaem
poluchaem
gde ![]() raspredeleno ravnomerno ot
raspredeleno ravnomerno ot ![]() do
do ![]() .
Kazhdaya iz fugkcii menyaetsya, no ansambl' kak celoe invarianten po otnosheniyu k
takomu preobrazovaniyu. Ostal'nye vysheprivedennye primery takzhe yavlyayutsya stacionarnymi.
.
Kazhdaya iz fugkcii menyaetsya, no ansambl' kak celoe invarianten po otnosheniyu k
takomu preobrazovaniyu. Ostal'nye vysheprivedennye primery takzhe yavlyayutsya stacionarnymi.
Ansambl' yavlyaetsya ergodicheskim, esli ot stacionaren i v nem otsutstvuyut podmnozhestva s veroyatnost'yu, otlichnoi ot 0 i 1, kotorye yavlyayutsya stacionarnymi. Ansambl'
yavlyaetsya ergodicheskim. Ni odno iz ego podmnozhestv s veroyatnost'yu ![]() ne perehodit v sebya
pri proizvol'nom sdvige po vremeni. S drugoi storony, ansambl'
ne perehodit v sebya
pri proizvol'nom sdvige po vremeni. S drugoi storony, ansambl'
s normal'no raspredelennoi ![]() i ravnomerno -
i ravnomerno - ![]() stacionaren, no ne ergodichen, tak kak, k primeru, ego podmnozhestvo s
stacionaren, no ne ergodichen, tak kak, k primeru, ego podmnozhestvo s
![]() mezhdu 0 i 1 stacionarno.
mezhdu 0 i 1 stacionarno.
Sredi vysheprivedennyh primerov tretii i chetvertyi ergodichny, pyatyi, vozmozhno, tozhe. Esli ansambl' ergodichen, mozhno (grubo) schitat', chto lyubaya iz ego fknkcii yavlyaetsya dlya nego tipichnoi. Bolee tochno, izvestno, chto dlya ergodicheskogo ansabmlya srednee lyuboi statistiki po ansamblyu ravno (s veroyatnost'yu 1) srednemu po vremeni dlya lyuboi iz funkcii (Eto - zamenitaya ergodicheskaya teorema (tochnee, odin iz ee aspektov), dokazannaya v nemnogo razlichnyh formulirovkah Birkovym, fon Neimanom i Kupmanom (Birkoff, von Neumann, Koopman), i obobshennaya zatem Vinerom, Hopfom, Gurevichem (Wiener, Hopf, Hurewicz) i drugimi. Literatura po ergodicheskoi teorii dostatochno obshirna, i my otsylaem chitatelya k stat'yam etih avtorov za tochnoi i obshei formulirovkoi; k primeru, sm. E. Hopf, ``Ergodentheorie,'' Ergebnisse der Mathematik und ihrer Grenzgebiete, v. 5; ``On Causality Statistics and Probability,'' Journal of Mathematics and Physics, v. XIII, No. 1, 1934; N. Wiener, ``The Ergodic Theorem,'' Duke Mathematical Journal, v. 5, 1939.). Grubo govorya, mozhno schitat', chto kazhdaya funkciya so vremenem prohodit s sootvetstvuyushei chastotoi vse elementy formy vseh ostal'nyh funkcii.
Tochno tak zhe, kak my proizvodim nekotorye operacii nad chislami ili funkciyami
dlya polucheniya novyh chisel lil funkcii, my mozhem proizvodit' nekotorye operacii
nad ansamblyami dlya polucheniya novyh. Pust', k primeru, u nas est' ansambl'
funkcii ![]() i operator
i operator ![]() , perevodyashii
kazhduyu iz funkcii
, perevodyashii
kazhduyu iz funkcii ![]() v
v ![]()
Meru veroyatnosti dlya mnozhestva ![]() opredelim cherez
meru dlya
opredelim cherez
meru dlya ![]() . Veroyatnost' nekotorogo podmnozhestva
. Veroyatnost' nekotorogo podmnozhestva
![]() ravna veroyatnosti ego proobraza iz
ravna veroyatnosti ego proobraza iz ![]() (to est' takogo podmnozhestva, kotoroe perevoditsya deistviem operatora
(to est' takogo podmnozhestva, kotoroe perevoditsya deistviem operatora ![]() v dannoe).
Fizicheski eto sootvetstvuet propuskaniyu ansamblya cherez nekotoroe ustroistvo,
k primeru - fil'tr, vypryamitel' ili modulyator. Funkcii na vyhode etogo
ustroistva obrazuyut ansambl'
v dannoe).
Fizicheski eto sootvetstvuet propuskaniyu ansamblya cherez nekotoroe ustroistvo,
k primeru - fil'tr, vypryamitel' ili modulyator. Funkcii na vyhode etogo
ustroistva obrazuyut ansambl' ![]() .
.
Ustroistvo ili operator ![]() nazovem invariantnym, esli sdvig
vhodnogo signala sootvetstvuyushim obrazom sdvigaet vyhodnoi, to est' iz
nazovem invariantnym, esli sdvig
vhodnogo signala sootvetstvuyushim obrazom sdvigaet vyhodnoi, to est' iz
sleduet
dlya vseh ![]() i
i ![]() . Legko pokazat' (sm. prilozhenie 5),
chto esli operator
. Legko pokazat' (sm. prilozhenie 5),
chto esli operator ![]() invarianten i vhodnoi ansambl' stacionaren,
vyhodnoi ansamblyu takzhe budet stacionarnym. Analogichno, esli vhodnoi ansambl'
ergodichen, budet ergodichnym i vyhodnoi.
invarianten i vhodnoi ansambl' stacionaren,
vyhodnoi ansamblyu takzhe budet stacionarnym. Analogichno, esli vhodnoi ansambl'
ergodichen, budet ergodichnym i vyhodnoi.
Fil'tr ili vypryamitel' invariantny otnositel'no lyubyh preobrazovanii vremeni, togda kak operaciya modulyacii - net, tak kak nesushaya chastota imeet opredelennuyu vremennuyu strukturu. Odnako, modulyaciya invariantna otnositel'no vseh preobrazovanii, kratnyh periodu nesushei chastoty.
Viner (Wiener) obratil vnimanie na glubokuyu svyaz' invariantnosti fizicheskih ustroistv otnositel'no vremennyh sdvigov s teoriei Fur'e (Teoriya svyazi obyazana Vineru osnovami svoi filosofii i teorii. Ego klassicheskii doklad (NDRC report) The Interpolation, Extrapolation and Smoothing of Stationary Time Series (Wiley, 1949) soderzhit pervuyu yasnuyu i chetkuyu formulirovku teorii svyazi kak statisticheskoi zadachi izucheniya operacii nad vremennymi ryadami. Eta rabota, hotya i posvyashennaya glavnym obrazom zadacham lineinogo predskazaniya i fil'tracii, yavlyaetsya vazhnym dopolneniem k dannoi stat'e. Hotelos' by takzhe otmetit' ego Cybernetics (Wiley, 1948), posvyashennuyu obshei zadache svyazi i upravleniya.). Tak, on pokazal, chto, esli ustroistvo yavlyaetsya lineinym i invariantnym, fur'e-analiz daet podhodyashii matematicheskii apparat dlya ego opisaniya.
Ansambl' funkcii yavlyaetsya podhodyashim matematicheskim predstavleniem soobshenii, vydavaemyh nepreryvnym istochnikom (k primeru, rechi), signalov, sformirovannyh preobrazovatelem, i vozmushayushego shuma. Teoriya svyazi v korrektnoi formulirovke, kak bylo otmecheno Vinerom, dolzhna imet' delo ne s konkretnymi funkciyami, a s ih ansamblyami. Sistema svyazi dolzhna razrabatyvat'sya ne dlya konkretnoi rechevoi funkcii, i uzh tem bolee ne dlya sinusoidal'nogo signala, a dlya ansamblya funkcii rechi.
Ansambli funkcii s ogranichennym diapazonom chastot
Esli funkciya vremeni ![]() ogranichena intervalom chastot ot
ogranichena intervalom chastot ot ![]() do
do ![]() , to ona polnost'yu opredelyaetsya naborom
svoih znachenii v diskretnom nabore tochek s shagom
, to ona polnost'yu opredelyaetsya naborom
svoih znachenii v diskretnom nabore tochek s shagom ![]() sposobom,
predstavlennym v nizheprivedennoi teoreme (Za dokazatel'stvom i obsuzhdeniem
otsylaem k rabote avtora ``Communication in the Presence of
Noise'', opublikovannoi v Proceedings of the Institute of Radio Engineers,
v. 37, No. 1, Jan., 1949, pp. 10--21.).
sposobom,
predstavlennym v nizheprivedennoi teoreme (Za dokazatel'stvom i obsuzhdeniem
otsylaem k rabote avtora ``Communication in the Presence of
Noise'', opublikovannoi v Proceedings of the Institute of Radio Engineers,
v. 37, No. 1, Jan., 1949, pp. 10--21.).
Teorema 13:
Pust' ![]() ne soderzhit komponent s chastotoi, bol'shei
ne soderzhit komponent s chastotoi, bol'shei ![]() . Togda
. Togda
gde
V etom razlozhenii ![]() predstavlyaetsya summoi ortogonal'nyh
funkcii. Koefficienty
predstavlyaetsya summoi ortogonal'nyh
funkcii. Koefficienty ![]() mozhno rassmatrivat' kak koordinaty
v beskonechnomernom ``prostranstve funkcii'', v kotorom kazhdaya funkciya sootvetstvuet
tol'ko odnoi tochke, i kazhdaya tochka - funkcii.
mozhno rassmatrivat' kak koordinaty
v beskonechnomernom ``prostranstve funkcii'', v kotorom kazhdaya funkciya sootvetstvuet
tol'ko odnoi tochke, i kazhdaya tochka - funkcii.
Funkciyu mozhno schitat' ogranichennoi vremenem ![]() , esli vse
ee znacheniya
, esli vse
ee znacheniya ![]() za predelami etogo intervala ravny nulyu.
Takim obrazom, funkcii, ogranichennye chastotnym diapazonom
za predelami etogo intervala ravny nulyu.
Takim obrazom, funkcii, ogranichennye chastotnym diapazonom ![]() i
vremennym -
i
vremennym - ![]() , sootvetstvuyut tochkam prostranstva
razmernosti
, sootvetstvuyut tochkam prostranstva
razmernosti ![]() .
.
Podmnozhestvo takih funkcii sootvetstvuet oblasti v etom prostranstve. K primeru,
funkcii s polnoi energiei, men'shei ![]() , sootvetstvuyut tochkam
vnutri
, sootvetstvuyut tochkam
vnutri ![]() -mernoi sfery radiusa
-mernoi sfery radiusa ![]() .
.
Ansambl' funkcii ogranichennyh dliny i chastotnogo diapazona mozhno
predstavit' raspredeleniem veroyatnosti ![]() v sootvetstvuyushem
v sootvetstvuyushem
![]() -mernom prostranstve. Esli zhe ansambl' ne ogranichen vo vremeni,
mozhno schitat', chto
-mernom prostranstve. Esli zhe ansambl' ne ogranichen vo vremeni,
mozhno schitat', chto ![]() koordinat na intervale
koordinat na intervale ![]() predstavlyayut chast' funkcii, lezhashuyu na etom intervale, a raspredelenie veroyatnosti
predstavlyayut chast' funkcii, lezhashuyu na etom intervale, a raspredelenie veroyatnosti
![]() - statisticheskuyu strukturu ansamblya intervalov
takoi dliny.
- statisticheskuyu strukturu ansamblya intervalov
takoi dliny.
Entropiya nepreryvnogo raspredeleniya
Entropiya diskretnogo nabora veroyatnostei ![]() byla opredelena
kak
byla opredelena
kak
Opredelim analogichno i entropiyu nepreryvnogo raspredeleniya s plotnost'yu
![]()
Dlya ![]() -mernogo raspredeleniya
-mernogo raspredeleniya ![]() imeem
imeem
Pri nalichii dvuh argumentov ![]() i
i ![]() (kotorye, v svoyu
ochered' mogut byt' mnogomernymi) sovmestnaya i uslovnaya entropii imeyut vid
(kotorye, v svoyu
ochered' mogut byt' mnogomernymi) sovmestnaya i uslovnaya entropii imeyut vid
i
gde
Entropii nepreryvnyh rasperedelii sohranyayut bol'shinstvo (no ne vse) svoistv diskretnogo sluchaya. V chastnosti,
-
Esli
 ogranicheno nekotorym ob'emom prostranstva
ogranicheno nekotorym ob'emom prostranstva  ,
to
,
to 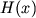 maksimal'no i ravno
maksimal'no i ravno 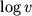 kogda
kogda 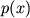 postoyanno (i ravno
postoyanno (i ravno 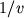 ) v etom ob'eme.
) v etom ob'eme.
-
Dlya lyu'yh dvuh peremennyh
 ,
, 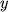 imeem
imeem
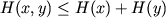
prichem ravenstvo imeet mesto togda i tol'ko togda, kogda
 i
i 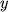 nezavisimy, to est'
nezavisimy, to est' 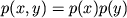 (za isklyucheniem nabora tochek
nulevoi veroyatnosti).
(za isklyucheniem nabora tochek
nulevoi veroyatnosti).
-
Rassmotrim obobshennuyu operaciyu usredneniya vida
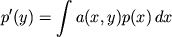
s
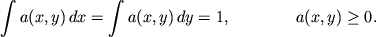
Togda entropiya usrednennogo raspredeleniya
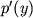 ne men'she
entropii ishodnogo
ne men'she
entropii ishodnogo 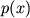 .
.
-
Imeet mesto
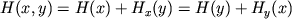
i
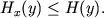
-
Pust'
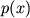 - odnomernoe raspredelenie. Formoi ego, maksimiziruyushei
entropiyu pri uslovii postoyanstva standartnogo otkloneniya
- odnomernoe raspredelenie. Formoi ego, maksimiziruyushei
entropiyu pri uslovii postoyanstva standartnogo otkloneniya 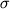 ,
yavlyaetsya gaussiana. Chtoby prodemonstrirovat' eto, maksimiziruem
,
yavlyaetsya gaussiana. Chtoby prodemonstrirovat' eto, maksimiziruem
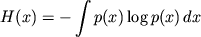 with
with
pri usloviyah
Eto trebuet, soglasno variacionnomu ischisleniyu, maksimizacii
![$$\int\bigl[-p(x)\log p(x)+\lambda p(x)x^2+\mu p(x)\bigr]\,dx.$$](https://images.astronet.ru/pubd/2003/04/04/0001188817/tex/formula432.gif)
Usloviem dlya etogo yavlyaetsya
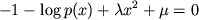
i sledovatel'no (podbiraya konstanty dlya udovletvoreniya ogranichenii)
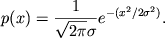
Analogichno, v sluchae
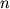 izmerenii, zafiksiruem vtorye momenty
izmerenii, zafiksiruem vtorye momenty
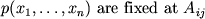 :
:
Togda entropiya maksimal'na (soglasno analogichnym vychisleniyam), kogda
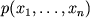 yavlyaetsya
yavlyaetsya 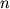 -mernym gaussovym raspredeleniem
so vtorymi momentami
-mernym gaussovym raspredeleniem
so vtorymi momentami 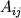 .
.
-
Entorpiya odnomernogo gaussova raspredeleniya so standartnym otkloneniem
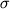 daetsya vyrazheniem
daetsya vyrazheniem
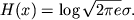
Ego mozhno vychislit' sleduyushim obrazom:
Analogichno,
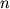 -mernoe gaussovo raspredelenie s sootvetstvuyushei
kvadratichnoi formoi
-mernoe gaussovo raspredelenie s sootvetstvuyushei
kvadratichnoi formoi 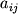 daetsya
daetsya
i entropiya mozhet byt' rasschitana kak
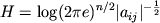
gde
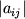 - opredelitel' s elementami
- opredelitel' s elementami 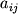 .
.
-
Esli
 ogranicheno polupryamoi (
ogranicheno polupryamoi (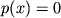 pri
pri 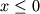 )
i pervyi moment
)
i pervyi moment  fiksirovan i raven
fiksirovan i raven  ,
,
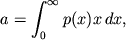
to maksimal'naya entropiya dostigaetsya pri
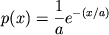
i ravna
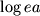 .
.
-
Est' odno sushestvennoe razlichie mezhdu nepreryvnoi i diskretnoi entorpiei. V diskretnom sluchae entropiya yavlyaetsya absolyutnoi meroi sluchainosti nekotoroi velichiny, togda kak v nepreryvnom eta mera
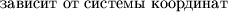 - v obshem sluchae ona izmenitsya pri izmenenii sistemy koordinat.
Tak, pri perehode k koordinatnoi sisteme entropiya
budet ravna
- v obshem sluchae ona izmenitsya pri izmenenii sistemy koordinat.
Tak, pri perehode k koordinatnoi sisteme entropiya
budet ravna
gde
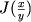 - yakobian preobrazovaniya koordinat.
Raskryvaya logarifm i perehodya k peremennym , poluchaem
- yakobian preobrazovaniya koordinat.
Raskryvaya logarifm i perehodya k peremennym , poluchaem
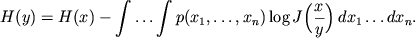
Takim obrazom, novaya entropiya men'she staroi na logarifm yakobiana. V nepreryvnom sluchae entropiyu mozhno schitat' meroi sluchainosti velichiny po otnosheniyu k prinyatomu etalonu, a imenno - k sisteme koordinat, v kotoroi vse malye elementy ob'ema imeyut ravnye vesa. Kogda my menyaem sistemu koordinat, entropiya v novoi sisteme harakterizuet sluchainost' pri ravnyh vesah ravnyh elementov ob'ema
Nesmotrya na etu zavisimost' ot sistemy koordinat ponyatie entropii v nepreryvnom sluchae tak zhe vazhno, kak i v diskretnom, blagodarya tomu, chto opredeleniya tempa informacii i propusknoi sposobnosti zavisyat ot raznosti dvuh entropii, kotoraya invariantna, tak kak kazhdaya iz nih izmenyaetsya na odnu i tu zhe velichinu.
Entropiya nepreryvnogo raspredeleniya mozhet byt' otricatel'noi. Shkala izmereniya ee imeet proizvol'nyi nol', sootvetstvuyushii ravnomernomu ob'emnomu raspredeleniyu. Bolee kompaktnoe, chem zhto, raspredelenie imeet men'shuyu entorpiyu, kotoraya otricatel'na. Tempy i propusknye sposobnosti, odnako, vsegda neotricatel'ny.
-
Chastnyi sluchai izmeneniya sistemy koordinat - lineinoe preobrazovanie
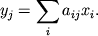
V etom sluchae yakobian raven prosto opredelitelyu
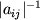 , i
, i
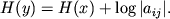
Pri povorote sistemy koordinat (ili lyubom drugom preobrazovanii, sohranyayushem dliny)
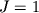 i
i 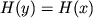 .
.
Entropiya ansamblya funkcii
Rassmotrim ergodicheskii ansambl' funkcii, ogranichennyh polosoi chastot shiriny $W$. Pust'
plotnost' funkcii raspredeleniya amplitud ![]() v
v
![]() posledovatel'nyh tochkah. Opredelim entropiyu ansamblya v raschete na stepen'
svobody kak
posledovatel'nyh tochkah. Opredelim entropiyu ansamblya v raschete na stepen'
svobody kak
Mozhno takzhe opredelit' entropiyu v sekundu, podeliv ne na ![]() , a na
vremya
, a na
vremya ![]() v
v ![]() vyborkah. Tak kak
vyborkah. Tak kak ![]() ,
,
![]() .
.
Pri belom teplovom shume ![]() gaussovo, i
gaussovo, i
Dlya dannoi srednei moshnosti ![]() belyi shum obladaet naibol'shei
vozmozhnoi entropiei, chto sleduet iz svoistv maksimizacii gaussova raspredeleniya,
otmechennyh vyshe.
belyi shum obladaet naibol'shei
vozmozhnoi entropiei, chto sleduet iz svoistv maksimizacii gaussova raspredeleniya,
otmechennyh vyshe.
Entropiya nepreryvnogo stohasticheskogo processa obladaet mnogimi svoistvami, analogichnymi diskretnomu sluchayu. V diskretnom sluchae entropiya byla svyazana s logarifmom veroyatnosti dlinnyh posledovatel'nostei i chislom dostatochno veroyatnyh posledovatel'nostei bol'shoi dliny. V nepreryvnom zhe sluchae ona svyazana pohozhim obrazom s logarifmom plotnosti veroyatnosti dlinnyh vyborok i ob'emom dostatochno bol'shoi veroyatnosti v prostranstve funkcii.
Bolee tochno, esli ![]() nepreryvno po vsem
nepreryvno po vsem ![]() dlya vseh
dlya vseh ![]() , to dlya dostatochno bol'shih
, to dlya dostatochno bol'shih ![]()
dlya vseh ![]() za isklyucheniem mnozhestva polnoi veroyatnosti
men'she
za isklyucheniem mnozhestva polnoi veroyatnosti
men'she ![]() , gde
, gde ![]() i
i ![]() proizvol'no
maly. Eto sleduet iz svoistva ergodichnosti pri delenii prostranstva na bol'shoe
chislo malen'kih yacheek.
proizvol'no
maly. Eto sleduet iz svoistva ergodichnosti pri delenii prostranstva na bol'shoe
chislo malen'kih yacheek.
Svyaz' ![]() s ob'emom mozhno ustanovit' sleduyushim obrazom. Pri teh zhe
usloviyah rassmotrim
s ob'emom mozhno ustanovit' sleduyushim obrazom. Pri teh zhe
usloviyah rassmotrim ![]() -mernoe prostranstvo, sootvetstvuyushee
-mernoe prostranstvo, sootvetstvuyushee
![]() . Pust'
. Pust' ![]() - naimen'shii ob'em
v etom prostranstve, soderzhashii v sebe polnuyu veroyatnost'
- naimen'shii ob'em
v etom prostranstve, soderzhashii v sebe polnuyu veroyatnost' ![]() .
Togda
.
Togda
pri ![]() ne ravno 0 ili 1.
ne ravno 0 ili 1.
Eto pokazyvaet, chto dlya bol'shih ![]() est' horosho opredelennyi ob'em
(kak minimum v logarifmicheskom smysle) bol'shoi veroyatnosti, i vnutri nego
plotnost' veroyatnosti dostatochno donorodna (opyat' zhe v logarifmicheskom smysle).
est' horosho opredelennyi ob'em
(kak minimum v logarifmicheskom smysle) bol'shoi veroyatnosti, i vnutri nego
plotnost' veroyatnosti dostatochno donorodna (opyat' zhe v logarifmicheskom smysle).
V sluchae belogo shuma fknkciya raspredeleniya daetsya vyrazheniem
Tak kak eto zavisit lish' ot ![]() , poverhnosti ravnoi
plotnosti veroyatnosti yavlyayutsya sferami i vse raspredelenie sfericheski-simmetrichno.
Oblast' bol'shoi veroyatnosti yavlyaetsya sharom radiusa
, poverhnosti ravnoi
plotnosti veroyatnosti yavlyayutsya sferami i vse raspredelenie sfericheski-simmetrichno.
Oblast' bol'shoi veroyatnosti yavlyaetsya sharom radiusa ![]() .
Pri
.
Pri ![]() veroyatnost' nahodit'sya vne etoi oblasti radiusa
veroyatnost' nahodit'sya vne etoi oblasti radiusa
![]() stremitsya k nulyu, i umnozhennyi na
stremitsya k nulyu, i umnozhennyi na ![]() logarifm ee ob'ema stremitsya k
logarifm ee ob'ema stremitsya k ![]() .
.
V nepreryvnom sluchae udobno rabotat' ne s entropiei ![]() ansamblya,
a s nekotoroi proizvodnoi ot nee velichinoi, kotoruyu my budem nazyvat'
moshnost'yu entropii. Opredelim ee kak moshnost' ogranichennogo tem zhe diapazonom
chastot belogo shuma toi zhe entropii. Inymi slovami, esli entropiya ansamblya
ravna
ansamblya,
a s nekotoroi proizvodnoi ot nee velichinoi, kotoruyu my budem nazyvat'
moshnost'yu entropii. Opredelim ee kak moshnost' ogranichennogo tem zhe diapazonom
chastot belogo shuma toi zhe entropii. Inymi slovami, esli entropiya ansamblya
ravna ![]() , to ee moshnost' est'
, to ee moshnost' est'
V geometricheskom podhode eto sootvetstvuet izmereniyu ob'ema vysokoi veroyatnosti kvadratom radiusa shara togo zhe ob'ema. Tak kak belyi shum imeet naibol'shuyu entropiyu, moshnost' entropii lyubogo shuma ne prevoshodit ego deistvitel'nuyu moshnost'.
| Usilenie | Faktor moshnosti entropii | Usilenie moshnosti entropii v decibelah | Impul'snyi otklik |
 | 2}$ | ||
 | |||
 | |||
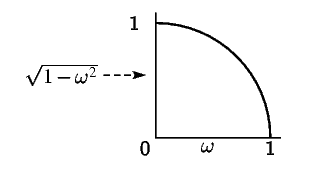 | |||
 | $\frac{1}{\alpha t^2}\bigl[\cos(1-\alpha)t-\cos t\bigr]$ |
Poteri entropii v lineinyh fil'trah
Teorema 14:
Pri propuskanii ansamblya s entropiei ![]() v raschete na stepen' svobody
v polose chastot
v raschete na stepen' svobody
v polose chastot ![]() cherez fil'tr s harakteristicheskoi funkciei $Y(f)$
entropiya vyhodnogo ansamblya ravna
cherez fil'tr s harakteristicheskoi funkciei $Y(f)$
entropiya vyhodnogo ansamblya ravna
Deistvie fil'tra svoditsya k lineinomu preobrazovaniyu koordinat. Esli my
rassmotrim razlichnye chastotnye komponenty kak ishodnuyu sistemu koordinat,
novye chastotnye komponenty poluchayutsya iz nih umnozheniem na nekotorye faktory.
Matrica preobrazovaniya koordinat, sledovatel'no, diagonalizuetsya v terminah
etih koordinat. Yakobian preobrazovaniya togda (dlya ![]() sinusoidal'nyh
i
sinusoidal'nyh
i
Entropiya summy dvuh ansamblei
gde ![]() nahodyatsya na ravnyh drug ot druga rasstoyaniyah v polose chastot
nahodyatsya na ravnyh drug ot druga rasstoyaniyah v polose chastot ![]() . Eto imeet mesto v predele
. Eto imeet mesto v predele
Tak kak ![]() - konstanta, ee srednee znachenie ravno samoi velichine,
i, ispol'zuya teoremu ob izmenenii entropii pri preobrazovanii koordinat, poluchaem
iskomoe dokazatel'stvo. Takim obrazom, esli entropiya pervogo ansamblya ravna
- konstanta, ee srednee znachenie ravno samoi velichine,
i, ispol'zuya teoremu ob izmenenii entropii pri preobrazovanii koordinat, poluchaem
iskomoe dokazatel'stvo. Takim obrazom, esli entropiya pervogo ansamblya ravna
![]() , to vtorogo -
, to vtorogo -
Konechnaya moshnost' entropii ravna ishodnoi, pomnozhennoi na geometricheskoe srednee
usileniya fil'tra. Esli usilenie izmeryaetsya v decibelah (db), to moshnost' entropii
na vyhode okazhetsya bol'she vhodnoi na arifmeticheskoe srednee usileniya na ![]() .
.
V tablice 1 privedeny poteri moshnosti entropii (i perevedeny
v decibely) dlya nekotoryh ideal'nyh harakteristik usileniya. Krome togo, predstavleny
impul'snye otkliki etih fil'trov dlya ![]() v predpolozhenii, chto
faza ravna nulyu.
v predpolozhenii, chto
faza ravna nulyu.
Poteri entropii dlya mnogih inyh sluchaev mogut byt' polucheny iz
vysheprivedennyh. K primeru, faktor moshnosti entropii ![]() primenim
takzhe k lyubym harakteristikam usileniya, poluchennym iz
primenim
takzhe k lyubym harakteristikam usileniya, poluchennym iz ![]() proizvol'nym sohranyayushim meru preobrazovaniem
osi
proizvol'nym sohranyayushim meru preobrazovaniem
osi ![]() . K primeru, lineino vozrastayushee usilenie
. K primeru, lineino vozrastayushee usilenie ![]() (ili ``piloobraznyi zubec'') na intervale ot 0 do 1 vedet k tem zhe samym poteryam
entropii. Obratnoe usilenie privodit k obrasheniyu faktora, sledovatel'no,
dlya
(ili ``piloobraznyi zubec'') na intervale ot 0 do 1 vedet k tem zhe samym poteryam
entropii. Obratnoe usilenie privodit k obrasheniyu faktora, sledovatel'no,
dlya ![]() faktor raven
faktor raven ![]() . Vozvedenie usileniya
v lyubuyu stepen' privodit k vozvedeniyu v tu zhe stepen' faktora.
. Vozvedenie usileniya
v lyubuyu stepen' privodit k vozvedeniyu v tu zhe stepen' faktora.
Esli u nas est' dva ansamblya funkcii ![]() i
i ![]() ,
my mozhem obrazovat' novyi, ``slozhiv'' ih. Pust' pervyi ansambl' imeet plotnost'
veroyatnosti
,
my mozhem obrazovat' novyi, ``slozhiv'' ih. Pust' pervyi ansambl' imeet plotnost'
veroyatnosti ![]() , a vtoroi -
, a vtoroi - ![]() .
Togda plotnost' veroyatnosti ih summy daetsya vyrazheniem
.
Togda plotnost' veroyatnosti ih summy daetsya vyrazheniem
Fizicheski eto sootvetstvuet slozheniyu signalov ili shumov, opisyvaemyh ishodnymi ansamblyami.
Sleduyushii rezul'tat poluchaetsya v prilozhenii 6.
Teorema 15:
Pust' srednie moshnosti dvuh ansamblei sut' ![]() i
i ![]() ,
a moshnosti entropii -
,
a moshnosti entropii - ![]() i
i ![]() .
Togda moshnost' entropii ih summy,
.
Togda moshnost' entropii ih summy, ![]() , ogranichena
, ogranichena
Gaussovskii belyi shum imeet otlichitel'noe svoistvo, sostoyashee v tom, chto on mozhet poglotit' lyuboi drugoi signal ili shum pri ego dobavlenii, i rezul'tiruyushaya moshnost' entropii budet primerno ravna summe moshnostei belogo shuma i signala (izmeryaya ot srednei velichiny signala, ravnoi obychno nulyu), esli signal dostatochno mal po sravneniyu s shumom.
Rassmotrim ![]() -mernoe prostranstvo funkcii, sootvetstvuyushih
etim ansamblyam. Belyi shum sootvetstvuet sfericheskomu gaussovomu raspredeleniyu
v etom prostranstve, signal - nekotoromu drugomu, ne obyazatel'no gaussovomu ili
sfericheski-simmetrichnomu. Pust' vtorye momenty etogo raspredeleniya otnositel'no
centra tyazhesti sut'
-mernoe prostranstvo funkcii, sootvetstvuyushih
etim ansamblyam. Belyi shum sootvetstvuet sfericheskomu gaussovomu raspredeleniyu
v etom prostranstve, signal - nekotoromu drugomu, ne obyazatel'no gaussovomu ili
sfericheski-simmetrichnomu. Pust' vtorye momenty etogo raspredeleniya otnositel'no
centra tyazhesti sut' ![]() , to est', dlya plotnosti veroyatnosti
, to est', dlya plotnosti veroyatnosti
![]() ,
,
gde ![]() - koordinaty centra tyazhesti. Teper'
- koordinaty centra tyazhesti. Teper' ![]() - polozhitel'no opredelennaya kvadratichnaya forma, i my mozhet povernut' sistemu koordinat tak,
chtoby ee osi sovpadali s osyami etoi formy.
- polozhitel'no opredelennaya kvadratichnaya forma, i my mozhet povernut' sistemu koordinat tak,
chtoby ee osi sovpadali s osyami etoi formy. ![]() togda svoditsya k
diagonal'nomu vidu
togda svoditsya k
diagonal'nomu vidu ![]() .Potrebuem, chtoby vse
.Potrebuem, chtoby vse ![]() byli maly po sravneniyu s
byli maly po sravneniyu s ![]() , kvadratom radiusa sfericheski-simmetrichnogo
raspredeleniya.
, kvadratom radiusa sfericheski-simmetrichnogo
raspredeleniya.
V etom sluchae svertka signala s shumom daet primerno gaussovskoe raspredelenie, kotoromu sootvetstvuet kvadratichnaya forma
Moshnost' entropii takogo raspredeleniya imeet vid
ili, priblizhenno,
Poslednii chlen sootvetstvuet moshnosti signala, togda kak pervyi - moshnosti shuma.
<< Chast' 2. Diskretnyi zashumlennyi kanal | Oglavlenie | Chast' 4. Nepreryvnyi kanal >>
" align="absmiddle" width="673" height="760" >
|
Publikacii s klyuchevymi slovami:
matematika - informaciya - Shennon
Publikacii so slovami: matematika - informaciya - Shennon | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |