Klod Shennon: Matematicheskaya teoriya svyazi
<< Chast' 4. Nepreryvnyi kanal | Oglavlenie |
Chast' 5. Temp dlya nepreryvnogo istochnika
Funkcii rascheta tochnosti
V sluchae diskretnogo istochnika informacii my mogli vvesti opredelennyi temp ``proizvodstva'' informacii, a imenno - entropiyu sootvetstvuyushego stohasticheskogo processa. V nepreryvnom zhe sluchae situaciya gorazdo bolee zaputannaya. Vo-pervyh, nepreryvnaya peremennaya mozhet prinimat' beskonechnoe chislo znachenii i trebuet, sootvetstvenno, beskonechnogo chisla dvoichnyh znakov dlya svoego predstavleniya. Eto znachit, chto dlya peredachi informacii ot nepreryvnogo istochnika s vozmozhnost'yu tochnogo vosstanovleniya v tochke priema trebuetsya, v obshem sluchae, kanal beskonechnoi propusknoi sposobnost'yu. A tak kak obychno kanal zashumlen i, sledovatel'no, imeet ogranichennuyu propusknuyu sposobnost'yu, tochnaya peredacha nevozmozhna.
Odnako na samom dele vse ne tak ploho. Obychno nam ne trebuetsya tochnaya peredacha takoi informacii, dostatochno ee peredachi s nekotoroi konechnoi tochnost'yu. Vopros v tom, mozhem li my pripisat' nepreryvnomu istochniku opredelennyi temp proizvodstva informacii, esli my trebuem lish' nekotoruyu tochnost' vosstanovleniya ee v priemnike, izmerennuyu nadlezhashim obrazom? Estestvenno, s rostom trebuemoi tochnosti temp takzhe vozrastaet. Pokazhem, chto my v dostatochno obshem sluchae mozhem opredelit' temp, obladayushii svoistvom togo, chto, pri nadlezhashem kodirovanii informacii, vozmozhno peredat' etu informaciyu po kanalu s propusknoi sposobnost'yu, ravnoi etomu tempu, s zadannoi tochnost'yu. Kanal men'shei propusknoi sposobnosti dlya etogo nedostatochen.
Vo-pervyh, neobhodimo dat' obshuyu matematicheskuyu formulirovku ponyatiya tochnosti
peredachi. Rassmotrim nmozhestvo soobshenii dostatochnoi dliny ![]() .
Istochnik opisyvaetsya zadaniem plotnosti veroyatnosti (v sootvetstvuyushem prostranstve)
togo, chto budt vybrano dannoe soobshenie
.
Istochnik opisyvaetsya zadaniem plotnosti veroyatnosti (v sootvetstvuyushem prostranstve)
togo, chto budt vybrano dannoe soobshenie ![]() . Sistema svyazi harakterizuetsya
(s tochki zreniya vneshnego nablyudatelya) zadaniem uslovnoi veroyatnosti
. Sistema svyazi harakterizuetsya
(s tochki zreniya vneshnego nablyudatelya) zadaniem uslovnoi veroyatnosti ![]() togo, chto, pri vydache istochnikom soobsheniya
togo, chto, pri vydache istochnikom soobsheniya ![]() , v tochke priema budet
vosstanovleno
, v tochke priema budet
vosstanovleno ![]() . Sistema v celom (vklyuchaya istochnik i sistemu peredachi)
opisyvaetsya veroyatnost'yu
. Sistema v celom (vklyuchaya istochnik i sistemu peredachi)
opisyvaetsya veroyatnost'yu ![]() ishodnogo soobsheniya
ishodnogo soobsheniya ![]() i
vosstanovlennogo -
i
vosstanovlennogo - ![]() . Esli eta funkciya zadana, izvestny vse harakteristiki
sistemy s tochki zreniya tochnosti peredachi. Lyuboi raschet tochnosti dolzhen svodit'sya
k nekotoroi operacii nad
. Esli eta funkciya zadana, izvestny vse harakteristiki
sistemy s tochki zreniya tochnosti peredachi. Lyuboi raschet tochnosti dolzhen svodit'sya
k nekotoroi operacii nad ![]() ; operaciya eta dolzhna obladat'
kak minimum svoistvom uporyadochennosti, to est' o dvuh sistemah
; operaciya eta dolzhna obladat'
kak minimum svoistvom uporyadochennosti, to est' o dvuh sistemah ![]() i
i ![]() dolzhno byt' mozhno skazat', v sootvetstvii s etim kriteriem
tochnosti, chto libo (1) pervaya bolee tochna, libo (2) vtoraya bolee
tochna, ili zhe (3) ih tochnosti ravny. Eto znachit, chto kriterii tochnosti
mozhet byt' predstavlen chislennymi funkciyami
dolzhno byt' mozhno skazat', v sootvetstvii s etim kriteriem
tochnosti, chto libo (1) pervaya bolee tochna, libo (2) vtoraya bolee
tochna, ili zhe (3) ih tochnosti ravny. Eto znachit, chto kriterii tochnosti
mozhet byt' predstavlen chislennymi funkciyami
argumenty kotoryh mogut prinimat' znacheniya vseh vozmozhnyh funkcii veroyatnosti
![]()
Pokazhem teper', chto, pri dostatochno obshih i razumnyh usloviyah, funkciyu ![]() mozhno zapisat' kak usrednenie
mozhno zapisat' kak usrednenie ![]() po vsem znacheniyam
po vsem znacheniyam ![]() i
i ![]()
Dlya polucheniya etogo dostatochno prinyat', chto (1) istochnik i sistema ergodichny,
to est' dostatochno dlinnaya posledovatel'nost' s veroyatnost'yu 1 tipichna dlya
ansamblya, i chto (2) metod rascheta ``priemlem'' v tom smysle, chto ego
mozhno provesti na osnovanii tipichnyh vhodnogo i vyhodnogo soobshenii ![]() i
i
![]() , prichem s rostom dlin vyborok poluchennaya ocenka shoditsya s veroyatnost'yu 1
k tochnomu znacheniyu, kotoroe mozhet byt' rasschitano na osnovanii polnogo znaniya
, prichem s rostom dlin vyborok poluchennaya ocenka shoditsya s veroyatnost'yu 1
k tochnomu znacheniyu, kotoroe mozhet byt' rasschitano na osnovanii polnogo znaniya
![]() . Pust' metodom rascheta (ocenkoi) budet
. Pust' metodom rascheta (ocenkoi) budet ![]() .
Togda
.
Togda ![]() stremitsya (pri
stremitsya (pri ![]() ) k
nekotoroi konstante prakticheski dlya vseh
) k
nekotoroi konstante prakticheski dlya vseh ![]() iz vysokoveroyatnoi
oblasti sistemy
iz vysokoveroyatnoi
oblasti sistemy
i, krome togo, mozhno zapisat'
tak kak
chto i dokazyvaet vysheprivedennyi rezul'tat.
Funkciya ![]() imeet smysl ``rasstoyaniya'' mezhdu
imeet smysl ``rasstoyaniya'' mezhdu ![]() i
i
![]() (Eto, odnako, ne ``metrika'' v tochnom smysle, tak kak
v obshem sluchae ne udovletvoryaet usloviyam
(Eto, odnako, ne ``metrika'' v tochnom smysle, tak kak
v obshem sluchae ne udovletvoryaet usloviyam ![]() i
i
![]() ). Ona harakterizuet,
naskol'ko nezhelatel'no (soglasno nashemu kriteriyu tochnosti) poluchenie
). Ona harakterizuet,
naskol'ko nezhelatel'no (soglasno nashemu kriteriyu tochnosti) poluchenie ![]() pri peredache
pri peredache ![]() . Vysheprivedennyi obshii rezul'tat mozhno pereformulirovat'
sleduyushim obrazom: lyuboi priemlemyi metod rascheta mozhno predstavit' kak usrednenie
funkcii rasstoyaniya po mnozhestvu prinyatyh
. Vysheprivedennyi obshii rezul'tat mozhno pereformulirovat'
sleduyushim obrazom: lyuboi priemlemyi metod rascheta mozhno predstavit' kak usrednenie
funkcii rasstoyaniya po mnozhestvu prinyatyh ![]() i peredannyh
i peredannyh ![]() soobshenii, vzveshennyh soglasno veroyatnosti
soobshenii, vzveshennyh soglasno veroyatnosti ![]() dannoi pary
pri dostatochnoi dline
dannoi pary
pri dostatochnoi dline ![]() soobshenii.
soobshenii.
Privedem neskol'ko prostyh primerov sposobov rascheta tochnosti.
-
Kriterii naimen'shih kvadratov.
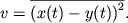
V dannoi chasto ispol'zuemoi mere funkciya rasstoyaniya
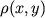 s tochnost'yu
do konstanty ravno kvadratu obychnogo evklidova rasstoyaniya mezhdu tochkami
s tochnost'yu
do konstanty ravno kvadratu obychnogo evklidova rasstoyaniya mezhdu tochkami  i
i 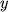 v sootvetstvuyushem prostranstve funkcii.
v sootvetstvuyushem prostranstve funkcii.
![$$\rho(x,y)=\frac1T\int_0^T\bigl[x(t)-y(t)\bigr]^2\,dt.$$](https://images.astronet.ru/pubd/2003/04/04/0001188817/tex/formula605.gif)
-
Kriterii vzveshennyh po chastote naimen'shih kvadratov. V bolee obshem sluchae mozhno ispol'zovat' v metode naimen'shih kvadratov razlichnye vesa dlya razlichnyh chastotnyh komponent. Eto ekvivalentno propuskaniyu raznosti
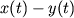 cherez fil'tr
nekotoroi formy i opredeleniyu zatem srednei vyhodnoi moshnosti. Potomu
cherez fil'tr
nekotoroi formy i opredeleniyu zatem srednei vyhodnoi moshnosti. Potomu
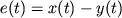
i
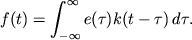
Togda
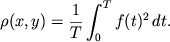
-
Kriterii absolyutnoi oshibki
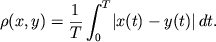
-
Struktura uha i mozga kosvennym obrazom opredelyaet sposob rascheta, ili, tochnee,
semeistvo takih sposobov, primenimyh v sluchae peredachi muzyki ili zvuka.
K primeru, eto kriterii ``ponyatnosti'', v kotorom
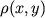 ravna
otnositel'noi chastote neverno interpretirovannyh slov pri prieme soobsheniya
ravna
otnositel'noi chastote neverno interpretirovannyh slov pri prieme soobsheniya 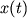 kak
kak 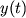 . I hotya my ne mozhem poluchit' yavnoe analiticheskoe vyrazhenie
dlya
. I hotya my ne mozhem poluchit' yavnoe analiticheskoe vyrazhenie
dlya 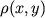 , ono v principe mozhet byt' opredeleno eksperimental'no.
Nekotorye ego svoistva sleduyut ih horosho izvestnyh svoistv sluha, k primeru,
togo, chto uho otnositel'no nechuvstvitel'no k faze, a chuvstvitel'nost' k chastote
i amplitude primerno logarifmicheskaya.
, ono v principe mozhet byt' opredeleno eksperimental'no.
Nekotorye ego svoistva sleduyut ih horosho izvestnyh svoistv sluha, k primeru,
togo, chto uho otnositel'no nechuvstvitel'no k faze, a chuvstvitel'nost' k chastote
i amplitude primerno logarifmicheskaya.
-
Diskretnyi sluchai mozhno rassmatrivat' kak chastnyi sluchai, v kotorom neyavno predpolagaetsya
raschet, osnovannyi na chastote oshibok. Funkciya
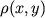 opredelyaetsya
togda kak chislo simvolov posledovatel'nosti
opredelyaetsya
togda kak chislo simvolov posledovatel'nosti 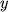 , otlichayushihsya ot
simvolov
, otlichayushihsya ot
simvolov  , delennoe na polnoe chislo simvolov v
, delennoe na polnoe chislo simvolov v  .
.
Temp istochnika po otnosheniyu k raschetu tochnosti
Samoe vremya opredelit' temp proizvodstva informacii nepreryvnym istochnikom.
Pust' zadany ![]() dlya istochnika i funkciya rascheta tochnosti
dlya istochnika i funkciya rascheta tochnosti
![]() , opredelyaemaya posredstvom rasstoyaniya
, opredelyaemaya posredstvom rasstoyaniya ![]() ,
kotoroe budem schitat' nepreryvnym kak po
,
kotoroe budem schitat' nepreryvnym kak po ![]() , tak i po
, tak i po ![]() .
Dlya opredelennogo
.
Dlya opredelennogo ![]() eta velichina ravna
eta velichina ravna
Bolee togo, temp vydachi dvoichnyh cifr, sootvetstvuyushih ![]() ,
,
Opredelim temp proizvodstva informacii ![]() dlya zadannoi tochnosti
dlya zadannoi tochnosti
![]() vosstanovleniya kak minimum
vosstanovleniya kak minimum ![]() pri fiksirovannoi
pri fiksirovannoi
![]() i var'irovanii
i var'irovanii ![]() , to est' kak
, to est' kak
pri uslovii
Eto znachit, chto my rassmatrivaem vse sistemy svyazi, kotorye mozhno ispol'zovat' dlya peredachi s zadannoi tochnost'yu. Temp peredachi v bitah v sekundu vychislyaetsya dlya kazhdoi iz nih. i my vybiraem tu, dlya kotoroi on minimalen. Etot temp my i pripisyvaem istochniku s zadannoi tochnost'yu.
Dokazatel'stvom etogo sluzhit sleduyushaya teorema.
Teorema 21:
Esli temp istochnika raven ![]() dlya tochnosti
dlya tochnosti ![]() ,
vydavaemuyu im informaciyu im mozhno zakodirovat' i peredat' po kanalu propusknoi
sposobnosti
,
vydavaemuyu im informaciyu im mozhno zakodirovat' i peredat' po kanalu propusknoi
sposobnosti ![]() s tochnost'yu, proizvol'no blizkoi k
s tochnost'yu, proizvol'no blizkoi k ![]() pri
pri ![]() . Eto nevozmozhno pri
. Eto nevozmozhno pri ![]() .
.
Poslednee utverzhdenie teoremy nemedlenno sleduet iz opredeleniya ![]() i predydushih rezul'tatov. Esli by eto bylo ne tak, mozhno bylo by peredat' bol'she,
chem
i predydushih rezul'tatov. Esli by eto bylo ne tak, mozhno bylo by peredat' bol'she,
chem ![]() bit v sekundu po kanalu propusknoi sposobnosti
bit v sekundu po kanalu propusknoi sposobnosti ![]() .
Pervaya zhe chast' mozhet byt' dokazana metodom, analogichnym ispol'zovannomu dlya
teoremy 11. My mozhem, vo-pervyh, razdelit' prostranstvo
.
Pervaya zhe chast' mozhet byt' dokazana metodom, analogichnym ispol'zovannomu dlya
teoremy 11. My mozhem, vo-pervyh, razdelit' prostranstvo ![]() na
bol'shoe chislo malen'kih yacheek i svesti zadachu k diskretnomu sluchayu. Eto izmenit
funkciyu rascheta tochnosti ne bolee chem na proizvol'no maloe chislo (pri dostatochno malom
razmere yacheek) blagodarya predpolozheniyu o nepreryvnosti
na
bol'shoe chislo malen'kih yacheek i svesti zadachu k diskretnomu sluchayu. Eto izmenit
funkciyu rascheta tochnosti ne bolee chem na proizvol'no maloe chislo (pri dostatochno malom
razmere yacheek) blagodarya predpolozheniyu o nepreryvnosti ![]() .
Pust'
.
Pust' ![]() - sistema, minimiziruyushaya temp i dayushaya
- sistema, minimiziruyushaya temp i dayushaya ![]() .
Vyberem iz vysokoveroyatnyh
.
Vyberem iz vysokoveroyatnyh ![]() sluchainyi nabor, soderzhashii
sluchainyi nabor, soderzhashii
elementov, gde ![]() pri
pri ![]() . Pri bol'shih
. Pri bol'shih
![]() kazhdaya iz vybrannyh tochek budet soedinena liniyami vysokoi veroyatnosti
(kak na ris.10) s naborom
kazhdaya iz vybrannyh tochek budet soedinena liniyami vysokoi veroyatnosti
(kak na ris.10) s naborom ![]() . Raschet, analogichnyi ispol'zovannomu
pri dokazatel'stve teoremy 11, pokazyvaet, chto pri bol'shih
. Raschet, analogichnyi ispol'zovannomu
pri dokazatel'stve teoremy 11, pokazyvaet, chto pri bol'shih ![]() prakticheski vse
prakticheski vse ![]() pokryvayutsya liniyami nabora
pokryvayutsya liniyami nabora ![]() pri
prakticheski lyubom vybore elementov
pri
prakticheski lyubom vybore elementov ![]() . Iskomaya sistema svyazi rabotaet tak.
Vybrannym tochkam sopostavlyayutsya dvoichnye chisla. Togda proizvol'noe soobshenie
. Iskomaya sistema svyazi rabotaet tak.
Vybrannym tochkam sopostavlyayutsya dvoichnye chisla. Togda proizvol'noe soobshenie
![]() budet (s veroyatnost'yu, stremyasheisya k edinice pri
budet (s veroyatnost'yu, stremyasheisya k edinice pri ![]() )
prinadlezhat' hotya by odnomu iz naborov, sootvetstvuyushih etim chislam. Sootvetstvuyushee
dvoichnoe chislo (ili proizvol'no vybrannoe, esli iz neskol'ko) peredaetsya po kanalu
s nadlezhashim kodirovaniem, dayushim maluyu veroyatnost' oshibki. Eto vozmozhno, tak
kak
)
prinadlezhat' hotya by odnomu iz naborov, sootvetstvuyushih etim chislam. Sootvetstvuyushee
dvoichnoe chislo (ili proizvol'no vybrannoe, esli iz neskol'ko) peredaetsya po kanalu
s nadlezhashim kodirovaniem, dayushim maluyu veroyatnost' oshibki. Eto vozmozhno, tak
kak ![]() . V tochke priema sootvetstvuyushee
. V tochke priema sootvetstvuyushee ![]() vosstanavlivaetsya
i schitaetsya prinyatym soobsheniem.
vosstanavlivaetsya
i schitaetsya prinyatym soobsheniem.
Harakteristika tochnosti ![]() dlya takoi sistemy mozhet byt' proizvol'no
blizkoi k
dlya takoi sistemy mozhet byt' proizvol'no
blizkoi k ![]() vyborom dostatochno bol'shogo
vyborom dostatochno bol'shogo ![]() , tak kak
dlya lyubyh dlinnyh vyborok peredannogo
, tak kak
dlya lyubyh dlinnyh vyborok peredannogo ![]() i prinyatogo soobshenii
i prinyatogo soobshenii
![]() ona stremitsya k
ona stremitsya k ![]() (s veroyatnost'yu 1).
(s veroyatnost'yu 1).
Interesno zametit', chto v dannoi sisteme shum vosstanovlennogo soobsheniya na samom dele vyzyvaetsya diskretizaciei v preobrazovatele, a ne shumom v kanale. Eto primerno sootvetstvuet shumu diskretizacii pri PCM-kodirovaniya.
Raschet tempov
Opredelenie tempa vo mnogih otnosheniyah analogichno opredeleniyu propusknoi sposobnosti. Tak, pervoe ravno
gde fiksirovany ![]() i ,
a vtoroe
i ,
a vtoroe
s fiksirovannoi ![]() i, vozmozhno, inymi ogranicheniyami (k primeru,
ogranicheniyami na srednyuyu moshnost') vida .
i, vozmozhno, inymi ogranicheniyami (k primeru,
ogranicheniyami na srednyuyu moshnost') vida .
Mozhno naiti chastnoe reshenie obshei zadachi maksimizacii dlya opredeleniya tempa istochnika. Ispol'zuya metod Lagranzha, rassmotrim
Variacionnoe uravnenie (pervaya variaciya ![]() ) privodit k
) privodit k
gde ![]() opredelyaetsya iz usloviya trebuemoi tochnosti, a
opredelyaetsya iz usloviya trebuemoi tochnosti, a ![]() -
dlya udovletvoreniya
-
dlya udovletvoreniya
Eto pokazyvaet, chto, pri nadlezhashem kodirovanii, uslovnaya veroyatnost' opredelennogo
proobraza dlya dannogo prinyatogo ![]() ,
, ![]() , ubyvaet
eksponencial'no s rostom funkcii rasstoyaniya mezhdu
, ubyvaet
eksponencial'no s rostom funkcii rasstoyaniya mezhdu ![]() i
i ![]() .
.
V special'nom sluchae zavisimosti funkcii rasstoyaniya ![]() lish'
ot (vektornoi) raznosti
lish'
ot (vektornoi) raznosti ![]() i
i ![]()
imeem
Sledovatel'no, ![]() yavlyaetsya konstantoi, skazhem,
yavlyaetsya konstantoi, skazhem, ![]() , i
, i
K sozhaleniyu, eto formal'nye resheniya trudnovychislimy v real'nyh situaciyah i ne imeyut bol'shogo znacheniya. Real'nye raschety byli dovedeny do konca lish' dlya neskol'kih prostyh sluchaev.
Esli funkciya rasstoyaniya ![]() ravna srednemu kvadratu
raznosti
ravna srednemu kvadratu
raznosti ![]() i
i ![]() i ansambl' shuma - belyi shum, temp
mozhet byt' opredelen. V etom sluchae imeem
i ansambl' shuma - belyi shum, temp
mozhet byt' opredelen. V etom sluchae imeem
gde ![]() . No
. No ![]() imeet mesto,
esli
imeet mesto,
esli ![]() - belyi shum, i ravno
- belyi shum, i ravno ![]() , gde
, gde
![]() - shirina diapazona chastot ansamblya soobsheniya. Togda
- shirina diapazona chastot ansamblya soobsheniya. Togda
gde ![]() - srednyaya moshnost' soobsheniya. Eto dokazyvaet sleduyuushee:
- srednyaya moshnost' soobsheniya. Eto dokazyvaet sleduyuushee:
Teorema 22:
Temp dlya istochnika belogo shuma moshnost'yu ![]() v diapazone
v diapazone ![]() op otnosheniyu k mere tochnosti naimen'shih kvadratov raven
op otnosheniyu k mere tochnosti naimen'shih kvadratov raven
gde ![]()
V obshem sluchae dlya lyubogo istochnika my mozhem poluchit' neravenstva, ogranichivayushie temp po otnosheniyu k kriteriyu naimen'shih kvadratov dlya oshibok.
Teorema 23:
Temp lyubogo istochnika diapazona chastot ![]() ogranichen neravenstvami
ogranichen neravenstvami
gde ![]() - srednyaya moshnost' istochnika,
- srednyaya moshnost' istochnika, ![]() - ego
moshnost' entropii, i
- ego
moshnost' entropii, i ![]() - dopustimyi srednii kvadrat oshibki.
- dopustimyi srednii kvadrat oshibki.
Nizhnii predel sleduet iz togo, chto ![]() dlya dannogo
dlya dannogo ![]() imeet mesto dlya belogo shuma; verhnii zhe mozhet byt' poluchen pri razmeshenii tochek
(ispol'zovannyh pri dokazatel'stve teoremy 21) ne luchshim, a sluchainym obrazom
vnutri sfery radiusa
imeet mesto dlya belogo shuma; verhnii zhe mozhet byt' poluchen pri razmeshenii tochek
(ispol'zovannyh pri dokazatel'stve teoremy 21) ne luchshim, a sluchainym obrazom
vnutri sfery radiusa ![]() .
.
Prilozhenie 5
Pust' ![]() - nekotoroe izmerimoe podmnozhestvo ansamblya
- nekotoroe izmerimoe podmnozhestvo ansamblya ![]() ,
a
,
a ![]() - podmnozhestvo ansamblya
- podmnozhestvo ansamblya ![]() , perehodyashee v
, perehodyashee v ![]() pod deistviem operacii
pod deistviem operacii ![]() . Togda
. Togda
Pust' ![]() - operator, sdvigayushii vse funkcii mnozhestva na
vremya
- operator, sdvigayushii vse funkcii mnozhestva na
vremya ![]() . Togda
. Togda
tak kak ![]() - invariant, i, sledovatel'no, kommutiruet s
- invariant, i, sledovatel'no, kommutiruet s ![]() .
Takim obrazom, esli
.
Takim obrazom, esli ![]() - mera veroyatnosti mnozhestva
- mera veroyatnosti mnozhestva ![]() ,
,
gde vtoroe ravenstvo sleduet iz opredeleniya mery v prostranstve ![]() ,
tret'e - iz stacionarnosti ansamblya
,
tret'e - iz stacionarnosti ansamblya ![]() , i poslednee - vnov' iz opredeleniya
mery na
, i poslednee - vnov' iz opredeleniya
mery na ![]() .
.
Dlya dokazatel'stva togo, chto svoistvo ergodichnosti sohranyaetsya pri invariantnyh
preobrazovaniyah, rassmotrim podmnozhestvo ![]() ansamblya
ansamblya ![]() ,
invariantnoe otnositel'no
,
invariantnoe otnositel'no ![]() , i mnozhestvo
, i mnozhestvo ![]() vseh
funkcii
vseh
funkcii ![]() , perehodyashih v
, perehodyashih v ![]() . Togda
. Togda
tak chto ![]() yavlyaetsya podmnozhestvom
yavlyaetsya podmnozhestvom ![]() pri
vseh
pri
vseh ![]() . Teper'
. Teper'
otkuda sleduet
dlya vseh ![]() s
s ![]() . Eto protivorechie
pokazyvaet, chto
. Eto protivorechie
pokazyvaet, chto ![]() ne sushestvuet.
ne sushestvuet.
Prilozhenie 6
Verhnii predel, ![]() , sootvetstvuet tomu,
chto mansimal'no vozmozhnaya entropiya dlya moshnosti
, sootvetstvuet tomu,
chto mansimal'no vozmozhnaya entropiya dlya moshnosti ![]() daetsya
belym shumom. Moshnost' entropii togda ravna
daetsya
belym shumom. Moshnost' entropii togda ravna ![]() .
.
Dlya polucheniya nizhnego predela, rassmotrim dva raspredeleniya ![]() izmerenii
izmerenii ![]() i
i ![]() s moshnostyami entropii
s moshnostyami entropii
![]() i
i ![]() . Kakuyu formu dolzhny
prinimat'
. Kakuyu formu dolzhny
prinimat' ![]() i
i ![]() dlya minimizacii moshnosti entropii
dlya minimizacii moshnosti entropii
![]() ih svertki
ih svertki
Entropiya ![]() velichiny
velichiny ![]() daetsya vyrazheniem
daetsya vyrazheniem
Minimiziruem eto vyrazhenie pri usloviyah
Rassmotrim teper'
Esli ![]() var'iruetsya po nekotoromu argumentu
var'iruetsya po nekotoromu argumentu ![]() ,
variaciya
,
variaciya ![]() ravna
ravna
i
Var'irovanie ![]() provoditsya analogichno. Sledovatel'no, usloviem
minimuma budet
provoditsya analogichno. Sledovatel'no, usloviem
minimuma budet
Umnozhaya pervoe na ![]() , a vtoroe - na
, a vtoroe - na ![]() i
integriruya po
i
integriruya po ![]() , poluchaem
, poluchaem
ili, razreshaya otnositel'no ![]() i
i ![]() i delaya zamenu,
i delaya zamenu,
Pust' teper' raspredeleniya ![]() i
i ![]() - gaussovy
- gaussovy
Togda ![]() takzhe budet normal'no raspredeleno s kvadratichnoi
formoi
takzhe budet normal'no raspredeleno s kvadratichnoi
formoi ![]() . Esli formy, obratnye k dannym, sut'
. Esli formy, obratnye k dannym, sut' ![]() ,
, ![]() ,
, ![]() ,
to
,
to
Pokazhem, chto eti funkcii udovletvoryayut usloviyu minimizacii togda i tol'ko togda,
kogda ![]() , i, sledovatel'no, opredelyayut minimum
, i, sledovatel'no, opredelyayut minimum ![]() pri etih ogranicheniyah. Imeem
pri etih ogranicheniyah. Imeem
Eto dolzhno byt' ravno
chto trebuet ![]() . V etom sluchae
. V etom sluchae
![]() i oba uravneniya obrashayutsya v tozhdestva.
i oba uravneniya obrashayutsya v tozhdestva.
Prilozhenie 7
Oboznachim bolee obshii i strogii podhod k osnovnym opredeleniyam teorii svyazi.
Rassmotrim prostranstvo mery veroyatnosti, elementami kotorogo yavlyayutsya uporyadochennye
pary ![]() . Otozhdestvim peremennye
. Otozhdestvim peremennye ![]() i
i ![]() s vozmozhnymi peredavaemymi i prinyatymi signalami dostatochno bol'shoi dliny
s vozmozhnymi peredavaemymi i prinyatymi signalami dostatochno bol'shoi dliny ![]() .
Nazovem mnozhestvo tochek, u kotoryh
.
Nazovem mnozhestvo tochek, u kotoryh ![]() prinadlezhat podmnozhestvu
prinadlezhat podmnozhestvu
![]() polosoi po
polosoi po ![]() , i, analogichno, u kotoryh
, i, analogichno, u kotoryh
![]() prinadlezhit
prinadlezhit ![]() - polosoi po
- polosoi po ![]() .
Podelim
.
Podelim ![]() i
i ![]() na neperekryvayushiesya izmerimye
podmnozhestva
na neperekryvayushiesya izmerimye
podmnozhestva ![]() i
i ![]() , priblizhayushie temp peredachi
, priblizhayushie temp peredachi
![]()
gde
| - mera veroyatnosti polosy po | |
| - mera veroyatnosti polosy po | |
| - mera veroyatnosti peresecheniya etih polos. |
Dal'neishee delenie ne mozhet umen'shit' ![]() . Podelim
. Podelim ![]() na
na
na
na ![]() i pust'
i pust'
Zamenim v etoi summe (dlya peresecheniya ![]() ,
, ![]() )
)
na
Legko pokazat', chto, pri nashem ogranichenii na ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
i, sledovatel'no, summa vozrastaet. Sledovatel'no, razlichnye vozmozhnye
deleniya obrazuyut uporyadochennoe mnozhestvo, na kotorom ![]() monotonno
vozrastaet pri umen'shenii razmerov otdel'nyh chastei. My mozhem odnoznachno
opredelit'
monotonno
vozrastaet pri umen'shenii razmerov otdel'nyh chastei. My mozhem odnoznachno
opredelit' ![]() kak naimen'shii verhnii predel
kak naimen'shii verhnii predel ![]() i
zapisat' ego kak
i
zapisat' ego kak
Etot integral, ponimaemyi v vysheprivedennom smysle, vklyuchaet v sebya kak diskretnyi,
tak i nepreryvnyi sluchai, a takzhe mnogo drugih, nesvodimyh k etim dvum. Ochevidno,
chto, esli ![]() i
i ![]() nahodyatsya v odnoznachnom sootvetstvii,
to temp ot
nahodyatsya v odnoznachnom sootvetstvii,
to temp ot ![]() k
k ![]() raven tempu ot
raven tempu ot ![]() k
k ![]() .
Esli
.
Esli ![]() - lyubaya funkciya
- lyubaya funkciya ![]() (ne obyazatel'no imeyushaya
obratnuyu), to temp ot
(ne obyazatel'no imeyushaya
obratnuyu), to temp ot ![]() i
i ![]() ne men'she, chem ot
ne men'she, chem ot
![]() k
k ![]() , tak kak, pri raschete priblizhenii, delenie
, tak kak, pri raschete priblizhenii, delenie
![]() bolee melko, chem
bolee melko, chem ![]() . V bolee obshem sluchae, esli
. V bolee obshem sluchae, esli
![]() i
i ![]() svyazany ne funkcional'no, a statisticheski, to est'
esli u nas est' prostranstvo mery veroyatnosti
svyazany ne funkcional'no, a statisticheski, to est'
esli u nas est' prostranstvo mery veroyatnosti ![]() , to
, to ![]() .
Eto znachit, chto primenenie lyuboi operacii, dazhe statisticheskoi, k prinyatomu signalu
ne uvelichivaet
.
Eto znachit, chto primenenie lyuboi operacii, dazhe statisticheskoi, k prinyatomu signalu
ne uvelichivaet ![]() .
.
Drugim ponyatiem, kotoroe neobhodimo tochno opredelit' pri abstraktnoi formulirovke
yavlyaetsya ``temp razmernosti'', to est' srednyaya razmernost', trebuemaya dlya
vydeleniya elementa ansamblya za sekundu. V sluchae oganichennogo chastotnogo diapazona
dostatochno ![]() chisel v sekundu. Obshee opredelenie mozhet byt' dano sleduyushim
obrazom. Pust'
chisel v sekundu. Obshee opredelenie mozhet byt' dano sleduyushim
obrazom. Pust' ![]() - ansambl' funkcii, a
- ansambl' funkcii, a ![]() mera ``rasstoyaniya'' mezhdu
mera ``rasstoyaniya'' mezhdu ![]() i
i ![]() za vremya
za vremya ![]() (k primeru, v smysle naimen'shih kvadratov na etom intervale). Pust'
(k primeru, v smysle naimen'shih kvadratov na etom intervale). Pust' ![]() -
naimen'shee chislo elementov
-
naimen'shee chislo elementov ![]() , kotorye mozhno vybrat' tak, chto
vse elementy ansamblya (za isklyucheniem mnozhestva mery
, kotorye mozhno vybrat' tak, chto
vse elementy ansamblya (za isklyucheniem mnozhestva mery ![]() ) lezhat
v predelah
) lezhat
v predelah ![]() ot kak minimum odnogo iz vybrannyh. Takim obrazom,
my pokryli prostranstvo vplot' do rasstoyaniya
ot kak minimum odnogo iz vybrannyh. Takim obrazom,
my pokryli prostranstvo vplot' do rasstoyaniya ![]() za isklyucheniem
mnozhestva maloi mery
za isklyucheniem
mnozhestva maloi mery ![]() . Opredelim temp razmernosti
. Opredelim temp razmernosti ![]() ansamblya kak troinoi predel
ansamblya kak troinoi predel
Eto - obobshenie mery razmernosti, ispol'zuemoi v topologii, soglasuyusheesya s intuitivnym tempom razmernosti dlya prostyh ansamblei, dlya kotoryh ono ochevidno.
<< Chast' 4. Nepreryvnyi kanal | Oglavlenie |
|
Publikacii s klyuchevymi slovami:
matematika - informaciya - Shennon
Publikacii so slovami: matematika - informaciya - Shennon | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |