Astronet > O krivizne prostranstva

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

1.V svoih izvestnyh rabotah, posvyashennyh obshim kosmologicheskim voprosam, Einshtein[1] i De-Sitter[2] prihodyat k dvum myslimym tipam vselennoi; Einshtein poluchaet tak nazyvaemyi cilindricheskii mir, v kotorom prostranstvo[3] obladaet postoyannoi, ne menyayusheisya s techeniem vremeni kriviznoi, prichem radius krivizny svyazyvaetsya s obshei massoi materii, raspolozhennoi v prostranstve; De-Sitter poluchaet sharovoi mir, v kotorom uzhe ne tol'ko prostranstvo, no i ves' mir obladaet do izvestnoi stepeni harakterom mira postoyannoi krivizny[4]. Pri etom i Einshtein, i De-Sitter predpolagayut opredelennyi harakter tenzora materii, otvechayushii gipoteze nesvyazannosti materii i ee otnositel'nomu pokoyu, inache govorya, dostatochnoi malosti skorostei materii po sravneniyu s fundamental'noi skorost'yu[5], to est' so skorost'yu sveta.

Nastoyashaya zametka imeet cel'yu poluchit' cilindricheskii i sfericheskii mir kak chastnye tipy, vytekayushie ih nekotoryh obshih polozhenii, a zatem pokazat' vozmozhnost' polucheniya osobogo mira, krivizna kotorogo, postoyannaya otnositel'no treh prinyatyh za prostranstvennye koordinat, menyaetsya s techeniem vremeni , t.e. zavisit ot chetvertoi koordinaty, prinyatoi za vremennuyu; etot novyi tip vselennoi v ostal'nyh svoih svoistvah napominaet cilindricheskii mir Einshteina.

2.Predpolozheniya, kotorye my polozhim v osnovu nashih soobrazhenii, raspadayutsya na dva klassa. K pervomu klassu otnosyatsya predpolozheniya, odinakovye s temi, kotorye delayut Einshtein i De-Sitter i kotorye otnosyatsya k uravneniyam, upravlyayushim gravitacionnymi potencialami, i k harakteru sostoyaniya i dvizheniya materii v prostranstve. Ko vtoromu klassu otnosyatsya predpolozheniya ob obshem, tak skazat', geometricheskom haraktere nashego mira; iz prinyatoi nami gipotezy v vide chastnyh sluchaev mogut byt' polucheny kak cilindricheskii mir Einshteina, tak i sharovoi mir De-Sittera.

Predpolozheniya pervogo klassa sleduyushie:

1)gravitacionnye potencialy udovletvoryayut sisteme uravnenii Einshteina s tak nazyvaemym «kosmologicheskim» chlenom, kotoryi mozhet byt', v chastnosti, raven nulyu:

$R_{ik} - \frac12 g_{ik} R \pm \lambda g_{ik} = -\kappa T_{ik} \ \ \ \ \ \ (i,k=1,2,3,4),$

(A)

gde $g_{ik}$ - gravitacionnye potencialy, $T_{ik}$ - tenzor materii, $\kappa$ - nekotoraya postoyannaya, $R=g^{ik}R_{ik}$ , a tenzor $R_{ik}$ opredelyaetsya ravenstvom

$R_{ik} = \frac{\partial^2\ln{\sqrt{g}}}{\partial x_i \partial x_k} - \frac{\partial\ln{\sqrt{g}}}{\partial x_a} \left\{ ik \atop \sigma \right\} - \frac{\partial}{\partial x_{\sigma}} \left\{ ik \atop \sigma \right\} + \left\{i\alpha \atop \sigma \right\} \left\{ k\sigma \atop \alpha \right\},$

(B)

prichem $x_i$ $(i=1,2,3,4)$ - sut' mirovye koordinaty, a $\left\{ ik \atop \sigma \right\}$ - simvol Kristoffelya vtorogo roda[6];

2) materiya nahoditsya v nesvyazannom sostoyanii i obladaet vzaimno otnositel'nym pokoem; govorya menee strogo, otnositel'nye skorosti materii nichtozhny po sravneniyu so skorost'yu sveta. Pri takih predpolozheniyah tenzor materii $T_{ik}$ opredelyaetsya ravenstvami

$T_{ik}=0$ , esli $i$ i $k$ odnovremenno ne ravny 4,
$T_{44}=c^2\rho g_{44}$ , (C)

gde $\rho$ - plotnost' materii i $c$ - fundamental'naya skorost'; pri etom, konechno, mirovye koordinaty razdeleny na dve gruppy: $x_1,x_2,x_3$ nazvany prostranstvennymi koordinatami, a $x_4$ - vremennoi koordinatoi.

3. Predpolozheniya vtorogo klassa svodyatsya k sleduyushemu:

1) pri vydelenii ih chetyreh mirovyh koordinat treh prostranstvennyh ( $x_1,x_2,x_3$ ) my budem imet' prostranstvo postoyannoi krivizny, mogushei, odnako, menyat'sya s techeniem chetvertoi vremennoi koordinaty $x_4$ . Interval $ds$ [7], opredelyaemyi ravenstvom , mozhet byt' napisan pri pomoshi sootvetstvuyushego izmeneniya prostranstvennyh koordinat v sleduyushem vide:

$ds^2 = R^2(dx_1^2+\sin^2 x_1 dx_2^2 + \sin^2 x_1 \sin^2 x_2 dx_3^2) + 2g_{14} dx_1 dx_4 + 2g_{24} dx_2 dx_4 + 2g_{34} dx_3 dx_4 + g_{44} dx_4^2 \ ,$

gde $R$ est' funkciya tol'ko ot $x_4$ , $R$ proporcionalen radiusu krivizny prostranstva; takim obrazom, radius krivizny prostranstva mozhet menyat'sya s techeniem vremeni;

2) v vyrazhenii intervala $g_{14}, g_{24}, g_{34}$ obrashayutsya v nul' pri sootvetstvuyushem vybore vremennoi koordinaty, inache, kratko vyrazhayas', vremya ortogonal'no prostranstvu. Eto vtoroe predpolozhenie ne imeet, kak mne kazhetsya, v osnove svoei kakih-libo fizicheskih ili filosofskih soobrazhenii i vvoditsya isklyuchitel'no v celyah uprosheniya vychislenii. Neobhodimo zametit', chto miry Einshteina i De-Sittera yavlyayutsya chastnymi sluchayami rassmatrivaemogo predpolozheniya.

Predpolozheniya 1) i 2) dayut nam vozmozhnost' zapisat' $ds^2$ v vide

$ds^2 = R^2 (dx_1^2 + \sin^2 x_1 dx_2^2 + \sin^2 x_1 \sin^2 x_2 dx_3^2) + M^2dx_4^2$

(D)

gde $R$ zavisit tol'ko ot $x_4$ , a $M$ yavlyaetsya, voobshe govorya, funkciei vseh chetyreh mirovyh koordinat. Vselennaya Einshteina - chastnyi sluchai, poluchaemyi iz formuly (D) zamenoi $R^2$ na $-R^2/c^2$ i $M$ na 1, gde $R$ - postoyannyi (ne zavisyashii ot $x_4$ !) radius krivizny prostranstva. Vselennaya De-Sittera poluchaetsya, kogda v formule (D) zamenim $R^2$ na $-R^2/c^2$ , a $T$ - na $\cos{x_4}$ :

$d\tau^2 = -\frac{R}{c^2} (dx_1^2 + \sin^2 x_1 dx_2^2 + \sin^2 x_1 \sin^2 x_2 dx_3^2) + dx_4^2$

(D₁)

$d\tau^2 = -\frac{R^2}{c^2} (dx_1^2 + \sin^2 x_1 dx_2^2 + \sin^2 x_1 \sin^2 x_2 dx_3^2) + \cos^2 x_1 dx_4^2$

(D₂)

(Pridavaya intervalu $ds$ razmer vremeni, my oboznachim ego cherez $d\tau$ ; v etom sluchae postoyannaya $\kappa$ budet imet' razmernost'yu dlinu, delennuyu na massu i v edinicah CGS budet ravna $1.87\cdot10^{-27}$ )

4. Neobhodimo skazat' eshe neskol'ko slov o teh intervalah, v kotoryh zaklyucheny mirovye koordinat; inache govorya, neobhodimo uslovit'sya, kakie tochki mnogoobraziya chetyreh izmerenii my budem schitat' za razlichnye. Ne vhodya v bolee podrobnye poyasneniya, uslovimsya prostranstvennye koordinaty izmenyat' v sleduyushih intervalah: $x_1$ - v intervale $(0,\pi)$ , $x_2$ - v intervale $(0,\pi)$ , $x_3$ - v intervale $(0,2\pi)$ , chto zhe kasaetsya vremennoi koordinaty, to vopros ob intervale izmeneniya ee ostavim otkrytym. k nemu my vernemsya v dal'neishem.

$2

1.Pol'zuyas' uravneniyami (A) i (B) v predpolozhenii, chto gravitacionnye potencialy opredelyayutsya ravenstvom (D), i polagaya v uravneniyah (A), chto $i=1,2,3$ , $k=4$ , naidem

$R'(x_4)\frac{\partial M}{\partial x_1} = R'(x_4)\frac{\partial M}{\partial x_2} = R'(x_4) \frac{\partial M}{\partial x_3}.$

Eti ravenstva imeyut dva sluchaya: 1) $R'(x_4)=0$ , $R$ ne zavisit ot $x_4$ i yavlyaetsya postoyannoi; nazovem etot sluchai stacionarnym mirom, i 2) $R'(x_4)\neq 0$ , $M$ zavisit tol'ko ot $x_4$ ; nazovem etot sluchai nestacionarnym mirom.

Obrashayas' snachala k stacionarnomu miru, vypishem uravneniya (A) dlya $i,k=1,2,3$ v predpolozhenii razlichnyh indeksov; uravneniya eti dadut nam sleduyushuyu sistemu formul:

$\frac{\partial^2M}{\partial x_1 \partial x_2} - \ctg x_1 \frac{\partial M}{\partial x_2} = 0 ,$
$\frac{\partial^2M}{\partial x_1 \partial x_3} - \ctg x_1 \frac{\partial M}{\partial x_3} = 0 ,$
$\frac{\partial^2M}{\partial x_2 \partial x_3} - \ctg x_2 \frac{\partial M}{\partial x_3} = 0 .$

Integriruya eti uravneniya, naidem

$M = A(x_3,x_4) \sin x_1 \sin x_3 + B(x_3,x_4) \sin x_1 + C(x_1,x_4),$

(1)

gde $A,B,C$ - proizvol'nye funkcii svoih argumentov. Razreshaya obychnymi priemami uravneniya (A) otnositel'no tenzora , isklyuchaya iz neuchtennyh i neispol'zovannyh eshe uravnenii neizvestnuyu plotnost'[8] i podstavlyaya vyrazhenie (1) dlya $M$ v eti uravneniya, my posle dlinnyh, no elementarnyh vychislenii naidem, chto dlya $M$ vozmozhny sleduyushie dva vyrazheniya:

$M=M_0=\mbox{const},$

(2)

$M=(A_0x_4+B_0)\cos x_1,$

(3)

gde $M_0,A_0,B_0$ - postoyannye velichiny.

V sluchae, kogda $M$ ravno postoyannomu chislu, my imeem dlya stacionarnogo mira sluchai cilindricheskogo mira. Pri etom udobnee operirovat' gravitacionnymi potencialami, poluchaemymi iz formuly (D); opredelyaya plotnost' i velichinu $\lambda$ , poluchim izvestnyi rezul'tat Einshteina:

$\lambda=\frac{c^2}{R^2},\quad \rho=\frac2{\kappa R^2},\quad M=\frac{4\pi^2}{\kappa}R$

gde $M$ - obshaya massa vsego prostranstva.

V drugom vozmozhnom sluchae, kogda $M$ opredelyaetsya iz formuly (3), my pri pomoshi racional'nogo izmeneniya $x_4$ [9] prihodim k sharovomu miru De-Sittera, v kotorom $M=\cos x_1$ ; pol'zuyas' formuloi D₂, naidem sleduyushie sootnosheniya De-Sittera:

$\lambda=\frac{3c^2}{R^2}, \quad \rho=0, \quad M=0 .$

Takim obrazom, stacionarnyi mir mozhet byt' ili cilindricheskim mirom Einshteina, ili sfericheskim mirom De-Sittera.

2. Obratimsya teper' k izucheniyu drugogo vozmozhnogo mira - nestacionarnogo. V etom sluchae $M$ est' funkciya tol'ko $x_4$ ; sootvetstvenno izmenyaya $x_4$ , my mozhem bez ogranicheniya obshnosti polozhit' $M=1$ ; imeya v vidu bol'shie udobstva nashih obychnyh predstavlenii, napishem $ds^2$ v forme, analogichnoi (D₁) i (D₂):

$ds^2 = -\frac{R^2(x_4)}{c^2} (dx_1^2 + \sin^2 x_1 dx_2^2 + \sin^2 x_1 \sin^2 x_2 dx_3^2) + dx_4^2 .$

(D₃)

Nashei zadachei yavlyaetsya opredelenie $R$ i $\rho$ iz uravnenii (A). Ochevidno, chto uravneniya (A), v kotoryh znachki razlichny, nichego ne dadut; uravneniya (A), v kotoryh $i=k=1,2,3$ , dadut odno sootnoshenie:

$\frac{R'^2}{R^2}+\frac{2RR''}{R^2}+\frac{c^2}{R^2}-\lambda=0 ,$

(4)

a uravnenie (A), v kotorom $i=k=4$ , dast ravenstvo

$\frac{3R'^2}{R^2}+\frac{3c^2}{R^2}-\lambda=\kappa c^2\rho ,$

(5)

prichem

$R'=\frac{dR}{dx_4}, \quad R''=\frac{d^2R}{dx_4^2} .$

Tak kak $R''\neq0$ , to integrirovanie uravneniya (4) posle zameny dlya udobstva $x_4$ na $t$ dast nam uravnenie

$\frac1{c^2}\left(\frac{dR}{dt}\right)^2=\frac{A-R+\frac{\lambda}{3c^3}R^3}{R} ,$

(6)

gde $A$ - proizvol'naya postoyannaya. Iz etogo uravneniya $R$ poluchaetsya putem obrasheniya nekotorogo ellipticheskogo integrala, t.e. putem resheniya otnositel'no $R$ uravneniya

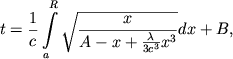$t=\frac1c\int\limits_a^R\sqrt{ \frac{x}{A-x+\frac{\lambda}{3c^3}x^3} }dx+B,$

(7)

gde $B$ i $a$ - postoyannye; pri etom, konechno, nado pomnit' ob obychnyh izmeneniya znaka u kvadratnogo kornya.

Uravnenie (5) daet nam vozmozhnost' opredelit' $\rho$ :

$\rho=\frac{3A}{\kappa R^3}$

(8)

cherez vsyu massy $M$ prostranstva; postoyannaya $A$ vyrazitsya ravenstvom

$A=\frac{\kappa M}{6\pi^2} ,$

(9)

prinimaya, chto massa $M$ - velichina polozhitel'naya, my i dlya $A$ poluchim polozhitel'noe znachenie.

3. Izuchenie nestacionarnogo mira osnovano na izuchenii uravnenii (6) i (7); pri etom, konechno, velichina $\lambda$ ne opredelyaetsya sama soboi, i my pri izuchenii uravnenii (6) i (7) budem predpolagat', chto $\lambda$ mozhet prinimat' lyubye znacheniya. Opredelim te znacheniya peremennoi $x$ , pri kotoryh kvadratnyi koren', vhodyashii v formulu (7), mozhet izmenit' svoi znak. Ogranichivayas' sluchaem polozhitel'nogo radiusa krivizny, nam dostatochno rassmotret' znacheniya dlya $x$ , pri kotoryh podkorennoe vyrazhenie obrashaetsya v nul' ili beskonechnost' v intervale $(0,\infty)$ dlya $x$ , t.e. dlya polozhitel'nyh $x$ .

Odno iz znachenii $x$ , pri kotorom kvadratnyi koren' v formule (7) obrashaetsya v nul', est' znachenie $x=0$ ; drugie znacheniya $x$ , pri kotoryh kvadratnyi koren' v formule (7) mozhet izmenyat' svoi znak, opredelyatsya pri izuchenii polozhitel'nyh kornei uravneniya

$A-x+\frac{\lambda}{3c^3}x^3=0 .$

Oboznachaya $\lambda/3c^3$ cherez $y$ , postroim semeistvo krivyh tret'ego poryadka v ploskosti $(x,y)$ , opredelyaemoe uravneniem

$yx^3-x+A=0 ,$

(10)

gde $A$ - parametr semeistva, menyayushiisya v intervale . Krivye nashego semeistva, pokazannye na risunke, peresekayut os' $x$ v tochke $x=A, y=0$ i imeyut maksimum v tochke

$x=\frac{3A}{2},\quad y=\frac{4}{27A^2} .$

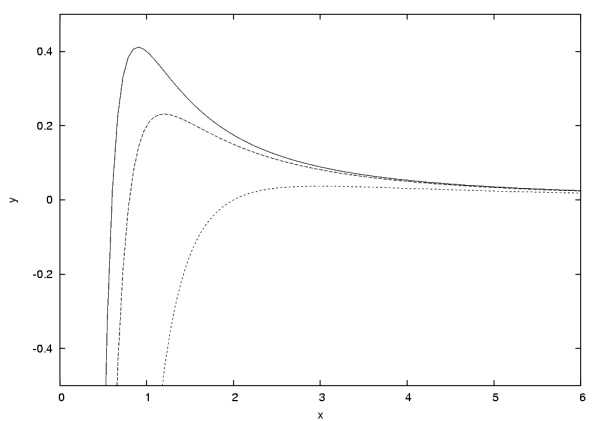
Rassmotrenie chertezha pokazyvaet, chto pri otricatel'nyh $\lambda$ uravnenie $A-x+(\lambda/3c^3)x^3=0$ imeet odin polozhitel'nyi koren' $x_0$ , lezhashii v intervale $(0,A)$ ; rassmatrivaya $x_0$ kak funkciyu $\lambda$ i $A$ :

$x_0=\theta(\lambda,A) ,$

naidem, chto $\theta$ - vozrastayushaya funkciya ot $\lambda$ i vozrastayushaya funkciya ot $A$ . Dalee, esli $\lambda$ lezhit v intervale , to uravnenie nashe budet imet' dva polozhitel'nyh kornya: i $x'_0=\phi(\lambda,A)$ , prichem $x_0$ lezhit v intervale $(A,\frac32A)$ , a $x'_0$ - v intervale $(\frac32A,\infty)$ ; $\theta(\lambda,A)$ budet vozrastayushei funkciei kak ot $\lambda$ , tak i ot $A$ ; budet ubyvayushei funkciei ot $\lambda$ i ot $A$ . Nakonec, esli $\lambda$ bol'she $\frac49(c^2/A^2)$ , to nashe uravnenie ne budet imet' polozhitel'nyh kornei.

Pristupaya k issledovaniyu formuly (7), sdelaem odno zamechanie: pust' v nachal'nyi moment , t.e. pri $t=t_0$ , radius krivizny raven $R_0$ . V etot nachal'nyi moment kvadratnyi koren', stoyashii v formule (7), budet imet' znak plyus ili minus, smotrya po tomu, vozrastaet li radius krivizny s techeniem vremeni pri $t=t_0$ ili net. Izmenyaya vremya $t$ na $-t$ , my vsegda mozhem pripisat' etomu kvadratnomu kornyu znak plyus, inache govorya, bez ogranicheniya obshnosti, mozhem vremya vybrat' tak, chtoby radius krivizny v rassmatrivaemyi nachal'nyi moment $t=t_0$ vozrastal s techeniem vremeni.

4. Rassmotrim sluchai, kogda , kogda, sledovatel'no, uravnenie $A-x+(\lambda/3c^3)x^3 = 0$ ne imeet polozhitel'nyh kornei. V etom sluchae uravnenie (7) perepishetsya sleduyushim obrazom:

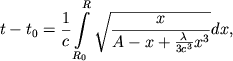$t-t_0=\frac1c\int\limits_{R_0}^{R}\sqrt{ \frac{x}{A-x+\frac{\lambda}{3c^3}x^3} }dx ,$

(11)

prichem, soglasno zamechaniyu, sdelannomu v konce predydushego punkta, kvadratnyi koren' budet vsegda polozhitelen. Otsyuda sleduet, chto $R$ budet vozrastayushei funkciei ot $t$ ; na nachal'noe znachenie radiusa krivizny $R_0$ nikakih v etom sluchae ogranichenii ne nalagaetsya.

Tak kak radius krivizny ne mozhet byt' men'she nulya, to, umen'shayas' ot $R_0$ s umen'sheniem $t$ soglasno formule (11), radius krivizny cherez nekotoryi promezhutok vremeni $t'$ doidet do nulya. Pol'zuyas' ochevidnoi analogiei, budem nazyvat' promezhutok vremeni, ponadobivshiisya, chtoby radius krivizny ot $0$ doshel do $R_0$ , vremenem, proshedshim ot sotvoreniya mira[10]; etot promezhutok $t'$ opredelyaetsya ravenstvom

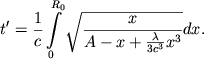$t'=\frac1c\int\limits_0^{R_0}\sqrt{ \frac{x}{ A-x+\frac{\lambda}{3c^3}x^3 } } dx .$

(12)

Uslovimsya v dal'neishem rassmatrivaemyi mir nazyvat' monotonnym mirom pervogo roda.

Vremya, proshedshee ot sotvoreniya monotonnogo mira pervogo roda, rassmatrivaemoe kak funkciya $R_0,A,\lambda$ , obladaet sleduyushimi svoistvami: 1) ono vozrastaet s uvelicheniem $R_0$ ; 2) ono ubyvaet s uvelicheniem $A$ , to est' s uvelicheniem massy materii prostranstva; 3) ono ubyvaet s uvelicheniem $\lambda$ . Esli $A>\frac23 R_0$ , to pri lyubyh $\lambda$ vremya, protekshee ot «sotvoreniya mira», konechno, esli $A \leq \frac23R_0$ , to vsegda naidetsya takoe harakteristicheskoe znachenie $\lambda=\lambda_1=\frac49 (c^2/A^2)$ , chto s priblizheniem $\lambda$ k etoi velichine vremya, proshedshee ot «sotvoreniya mira», budet bespredel'no vozrastat'.

5. Polozhim dalee, chto $\lambda$ zaklyucheno v intervale $(0,\frac49(c^2/A^2))$ ; togda nachal'noe znachenie radiusa krivizny $R_0$ mozhet lezhat' v odnom iz treh intervalov: $(0,x_0),(x_0,x'_0),(x'_0,\infty)$ . Esli $R_0$ lezhit v intervale $(x_0,x'_0)$ , to kvadratnyi koren' v formule (7) imeet mnimoe znachenie i prostranstvo s takoi nachal'noi kriviznoi ne mozhet sushestvovat'. Sluchai, kogda $R_0$ lezhit v intervale $(0,x_0)$ , my rassmotrim v sleduyushem punkte, teper' zhe ostanovimsya na tret'em sluchae, kogda $R_0>x'_0$ ili $R_0>\phi(\lambda,A)$ . V etom sluchae rassuzhdeniyami, analogichnymi privedennym v predydushem punkte, mozhno pokazat', chto $R$ budet vozrastayushei funkciei vremeni, prichem $R$ mozhet menyat'sya, nachinaya s $x'_0=\phi(\lambda,A)$ ; promezhutok vremeni, proshedshii s momenta, kogda $R=x_0$ , do momenta $R=R_0$ , nazovem vremenem, protekshim ot «sotvoreniya mira», i oboznachim cherez $t'$ :

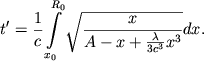$t'=\frac1c\int\limits_{x_0}^{R_0}\sqrt{ \frac{x}{ A-x+\frac{\lambda}{3c^3}x^3 } } dx .$

(13)

Uslovimsya rassmatrivaemyi mir nazyvat' monotonnym mirom vtorogo roda.

6. Rassmotrim, nakonec, sluchai, kogda $\lambda$ zaklyucheno v intervale $(-\infty,0)$ . V etom sluchae, esli $R_0>x_0=\theta(\lambda,A)$ , to kvadratnyi koren' v formule (7) stanovitsya mnimym, i, sledovatel'no, prostranstvo s ukazannym radiusom krivizny ne mozhet sushestvovat'. Esli $R_0 \lt x_0$ , to rassmatrivaemyi sluchai budet sovershenno odinakov so sluchaem, opushennym pri rassmotrenii v predydushem punkte. Itak, polozhim, chto $\lambda$ lezhit v intervale $(-\infty,\frac49(c^2/A^2))$ , a $R_0 \lt x_0$ . Obychnymi rassuzhdeniyami[11] mozhno v etom sluchae pokazat', chto $R$ budet periodicheskoi funkciei ot $t$ s periodom $t_p$ , kotoryi my nazovem periodom mira i kotoryi budet opredelen ravenstvom

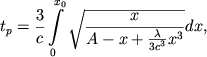$t_p=\frac3c\int\limits_0^{x_0}\sqrt{ \frac{x}{ A-x+\frac{\lambda}{3c^3}x^3 } } dx ,$

(14)

prichem radius mira budet menyat'sya ot nulya do $x_0$ . Uslovimsya takogo roda mir nazyvat' periodicheskim. Period periodicheskogo mira vozrastaet s vozrastaniem $\lambda$ , stremyas' k beskonechnosti, kogda $\lambda$ stremitsya k $\lambda_1=\frac49(c^2/A^2)$ .

Pri malyh $\lambda$ period $t_p$ opredelyaetsya priblizitel'noi formuloi

$t_p=\frac{\pi A}{c}$

(15)

Na periodicheskii mir mozhno smotret' s dvuh tochek zreniya. Esli schitat' dva yavleniya sovpadayushimi, kol' skoro sovpadayut prostranstvennye koordinaty, a vremennye otlichayutsya na celoe chislo periodov, to radius krivizny mira, uvelichivayas' snachala ot $0$ do $x_0$ , budet zatem umen'shat'sya do nulya: togda vremya sushestvovaniya mira budet konechnym.

S drugoi storony, esli izmenyat' vremya ot $-\infty$ do $\infty$ , t.e. esli schitat' dva yavleniya sovpadayushimi, kol' skoro sovpadayut ne tol'ko ih prostranstvennye koordinaty, no i ih vremennye koordinaty, to my pridem k deistvitel'noi periodichnosti krivizny prostranstva.

7. Dannye, kotorymi my raspolagaem, sovershenno nedostatochny dlya kakih-libo chislennyh podschetov i dlya resheniya voprosa o tom, kakim mirom yavlyaetsya nasha vselennaya; byt' mozhet, problema prichinnosti i problema centrobezhnoi sily prol'yut svet na rassmatrivaemye zdes' voprosy. Sleduet otmetit', chto v poluchennyh nami formulah «kosmologicheskaya» velichina $\lambda$ ne opredelyaetsya, yavlyayas' lishnei konstantoi zadachi; byt' mozhet, elektrodinamicheskie soobrazheniya smogut opredelit' etu velichinu. Polagaya $\lambda=0$ i schitaya $M$ ravnoi masse $5\cdot10^{21}$ nashih Solnc, budem dlya perioda mira imet' velichinu poryadka 10 milliardov let.

Eti cifry mogut imet', konechno, lish' illyustrativnoe znachenie.

1. Einstein A., Kosmologische Betrachtungen zur allgemien Relativistatstheorie, Sitzungsber, Dtsch. Akad. Berlin 1917
2. De-Sitter, On Einstein's theory of gravitation and its astronomical consequences, Monthly Notices Roy. Astron. Soc., 1916-1917
3. Pod «prostranstvom» budem podrazumevat' prostranstvo, opisyvaemoe mnogoobraziem treh izmerenii, otnosya termin «mir» k prostranstvu, opisyvaemomu mnogoobraziem chetyreh izmerenii
4. Klein F., Ueber die Integralform der Erhaltung ersatze und die Theorie der raumlichgeschlossen Welt, Gottinger Nach., 1918
5. Sm. etot termin u Eddingtona v knige Espace, Temps et Gravitation, 2 Partie. Paris, 1921, p.10
6. Znak $R_{ik}$ i skalyarnoi krivizny $R$ izmenen na obratnyi sravnitel'no s obychnym oboznacheniem etoi velichiny.
7. A. Eddington. Espace, Temps et Gravitation, 2 partie, Paris, 1921.
8. Plotnost' $\rho$ yavlyaetsya u nas neizvestnoi funkciei mirovyh koordinat $x_1,x_2,x_3,x_4$
9. Ukazannoe izmenenie proizvoditsya s pomosh'yu formuly: $d\tilde{x}_4=\sqrt{A_0x_4+B_0}dx_4$
10. Vremya, proshedshee ot sotvoreniya mira, harakterizuet vremya, proshedshee ot momenta, kogda prostranstvo bylo tochkoi ( $R=0$ ) do nyneshnego ego sostoyaniya ( $R=R_0$ )zh eto vremya mozhet byt' beskonechnym.
11. Sm., naprimer, Weierstrass K. Ueber eine Gattung der reel periodischer Functionen, Monastber. Konigl. Akad. Wiss., 1866, a takzhe Zur Theorie der kleinen endlichen Schwingungen, Z. Math. und Phys., 1902, 47. V nashem sluchae neobhodimo, konechno, vnesti nekotorye vidoizmeneniya v rassuzhdeniya citirovannyh avtorov; vprochem, periodichnost' v nashem sluchae ustanavlivaetsya putem elementarnogo rassmotreniya

Publikacii s klyuchevymi slovami: gravitaciya - Kosmologiya Publikacii so slovami: gravitaciya - Kosmologiya
Sm. takzhe: Padenie shara v Solnechnoi sisteme Razlozhenie dalekogo sveta Formirovanie galaktik v magnitnoi Vselennoi "Effekty" Zel'dovicha, zapechatlennye na nashem nebe Sverhnovaya 1994D i neozhidannaya Vselennaya Gravitacionnye anomalii na Merkurii Kuda smeshaetsya krasnoe smeshenie? Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

O krivizne prostranstva

Fridman A.A.

Petrograd, 29 maya 1922 g.

$1

$2