Reshenie zadachi o diametre globusa
2.03.1994 17:36 | Vselennaya i My

Sredi neskol'kih predlzhennyh reshenii naibolee original'nym i prakticheski vypolnimym bylo sleduyushee:

Voz'mem bol'shoi shkol'nyi cirkul'. Vyberem na poverhnosti shara lyubye dve tochki I i II. Iz etih tochek kak iz centrov provedem po dve okruzhnosti s poparno odinakovymi radiusami (ris. 1). Okruzhnosti peresekutsya v tochkah A, B, C, i D. Mozhno strogo dokazat' (no eto i tak vidno iz simmetrichnosti figury), chto eti tochki lezhat na odnom bol'shom kruge AB sfery-globusa. (Napomnim: bol'shim krugom na sfere nazyvaetsya krug, centr kotorogo sovpadaet s cetrom shara). V ploskosti etogo kruga (ris.2) tochki A, B, i C obrazuyut treugol'nik, vpisannyi v bol'shoi krug.

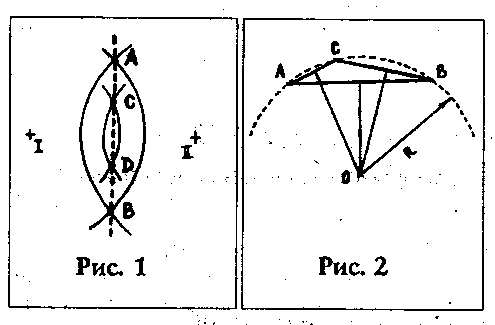
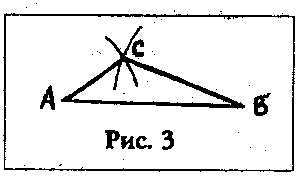
Dlya postroeniya treugol'nika ABC izmerim cirkulem dlinu otrezkov AB, BC i AC. Ochevidno, chto eti ne dugi na sfere, a hordy "vnutri shara" (ris.2). Kak izvestno iz geometrii, znaya tri storony treugol'nika, mozhno postroit' treugol'nik ABC (ris.3). Posle togo, kak treugol'nik postroen i nacherchen v nuzhnom masshtabe, sleduet opisat' vokrug nego okruzhnost'. (Kak eto sdelat', rasskazyvaetsya v uchebnike po geometrii). A nachertiv okruzhnost', mozhno izmerit' ee radius (ili diametr).

Pomnit'sya, v tot raz razmery poluchilis' sleduyushie: BC=77 sm; AC=56 sm; AB=125 sm. Diametr shara okazalsya ravnym primerno 3 m. Vprochem, vy sami mozhete ego utochnit'.

Mozhet byt', kto-to predlozhit drugoi, eshe bolee udobnyi sposob resheniya etoi zadachi.

Publikacii s klyuchevymi slovami: globus Publikacii so slovami: globus
Sm. takzhe: Goluboi Sharik Zemli s observatorii Suomi-NPP Lyubopytnaya zadacha