Chernaya dyra
1. Vvedenie
2. Pole tyagoteniya nevrashayusheisya
chernoi dyry
3. Pole tyagoteniya vrashayusheisya
chernoi dyry
4. Fizicheskie processy
v pole tyagoteniya chernoi dyry
1. Vvedenie
Chernaya dyra - oblast' prostranstva, v k-roi pole tyagoteniya nastol'ko sil'no, chto
vtoraya kosmich. skorost' (parabolicheskaya
skorost')
dlya nahodyashihsya v etoi oblasti tel dolzhna byla by prevyshat' skorost' sveta, t.e.
iz Ch.d. nichto ne mozhet vyletet' - ni izluchenie, ni chasticy, ibo v prirode nichto ne
mozhet
dvigat'sya so skorost'yu, bol'shei skorosti sveta. Granicu oblasti, za k-ruyu ne vyhodit
svet, naz. gorizontom Ch.d. Dlya togo chtoby pole tyagoteniya smoglo "zaperet'" izluchenie,
sozdayushee eto pole massa ![]() dolzhna szhat'sya do ob'ema s radiusom,
men'shim gravitacionnogo radiusa
dolzhna szhat'sya do ob'ema s radiusom,
men'shim gravitacionnogo radiusa ![]() . Gravitac. radius chrezvychaino mal dazhe dlya bol'shih mass (napr., dlya
Solnca, imeyushego massu
. Gravitac. radius chrezvychaino mal dazhe dlya bol'shih mass (napr., dlya
Solnca, imeyushego massu ![]() g,
g, ![]() 3 km).
3 km).
Pole tyagoteniya Ch.d. opisyvaetsya teoriei tyagoteniya Einshteina (sm. Tyagotenie). Soglasno etoi teorii, vblizi Ch.d. geometrich. sv-va prostranstva opisyvayutsya neevklidovoi (rimanovoi) geometriei, a vremya techet medlennee, chem vdali, vne sil'nogo polya tyagoteniya.
Po sovr. predstavleniyam, massivnye zvezdy (s massoi v nesk. ![]() i bol'she), zakanchivaya svoyu evolyuciyu, mogut v konce koncov szhat'sya (skollapsirovat')
i prevratit'sya v Ch.d. (sm. Evolyuciya zvezd,
Gravitacionnyi kollaps).
i bol'she), zakanchivaya svoyu evolyuciyu, mogut v konce koncov szhat'sya (skollapsirovat')
i prevratit'sya v Ch.d. (sm. Evolyuciya zvezd,
Gravitacionnyi kollaps).
Esli Ch.d. voznikaet pri szhatii nevrashayushegosya nezaryazhennogo tela, to ee vnesh. pole
tyagoteniya okazyvaetsya strogo sfericheskim i zavisyashim tol'ko ot polnoi massy tela
![]() . Vse otkloneniya ot sferichnosti v graivtac. pole pri obrazovanii Ch.d. izluchayutsya
v vide gravitac. voln (sm. Gravitacionnoe
izluchenie). Ostavsheesya pole ne zavisit ot raspredeleniya massy vnutri szhavshegosya
tela. T.o., hotya vnutri Ch.d. mozhet byt' "spryatano" ochen' nesimmetrichno szhimayusheesya
telo,
vnesh. pole tyagoteniya budet strogo sfericheski-simmetrichnym (t.n. pole Shvarcshil'da).
. Vse otkloneniya ot sferichnosti v graivtac. pole pri obrazovanii Ch.d. izluchayutsya
v vide gravitac. voln (sm. Gravitacionnoe
izluchenie). Ostavsheesya pole ne zavisit ot raspredeleniya massy vnutri szhavshegosya
tela. T.o., hotya vnutri Ch.d. mozhet byt' "spryatano" ochen' nesimmetrichno szhimayusheesya
telo,
vnesh. pole tyagoteniya budet strogo sfericheski-simmetrichnym (t.n. pole Shvarcshil'da).
Pri obrazovanii Ch.d. izluchayutsya takzhe vse fiz. polya, krome staticheskogo elektricheskogo polya (esli kollapsiruyushee telo bylo elektricheski zaryazhennym).
Esli telo, obrazovavshee Ch.d., vrashalos', to vokrug Ch.d. sohranyaetsya "vihrevoe" gravitac. pole, uvlekayushee vse tela vblizi Ch.d. vo vrashatel'noe dvizhenie vokrug nee. Eto pole opredelyaetsya pomimo massy Ch.d. tol'ko ee polnym momentom impul'sa. Pole tyagoteniya vrashayusheisya Ch.d. naz. polem Kerra.
2. Pole tyagoteniya nevrashayusheisya chernoi dyry
Dvizhenie tel v pole tyagoteniya Shvarcshil'da obladaet ryadom osobennostei. V teorii N'yutona
dvizhenie po okruzhnosti vokrug tyagoteyushego centra vozmozhno na lyubom rasstoyanii R
ot nego. V teorii Einshteina eto ne tak. Chem blizhe k Ch.d., tem bol'she skorost' krugovogo
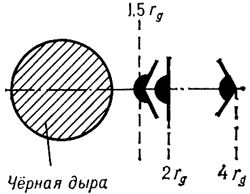
dvizheniya. Na okruzhnosti s R=1,5 rg skorost'
dvizheniya dostigaet svetovoi. Blizhe k Ch.d. dvizhenie po okruzhnosti, ochevidno, voobshe
nevozmozhno. V deistvitel'nosti zhe dvizhenie po okruzhnosti stanovitsya neustoichivym
na znachitel'no
bol'shih rasstoyaniyah, a imenno: nachinaya s R=3 rg,
kogda skorost' dvizheniya sostavlyaet vsego polovinu svetovoi. Tol'ko na rasstoyaniyah,
prevyshayushih 3rg, vozmozhno ustoichivoe krugovoe dvizhenie.
Na predele ustoichivosti krugovyh orbit energiya
svyazi chasticy ![]() , gde m - massa
chasticy.
, gde m - massa
chasticy.
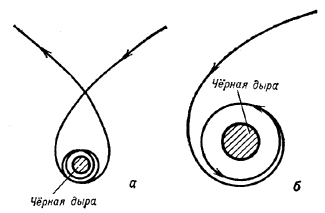
Osobyi interes predstavlyaet vozmozhnost' gravitac. zahvata chernoi dyroi tel, priletayushih iz beskonechnosti k tyagoteyushei masse, opisyvaet okolo nee parabolu ili giperbolu i (esli ne ispytyvaet soudareniya s tyagoteyushei massoi) snova uletaet v beskonechnost'. Gravitac. zahvat v etoi zadache nevozmozhen.
|
| Ris. 1. |
Nakonec, esli telo podoidet vplotnuyu k ukazannoi okruzhnosti, to ego orbita budet neogranichenno navivats'ya na okruzhnost'. Telo okazhetsya gravitacionno zahvachennym Ch.d. i nikogda snova ne uletit v kosmos (ris. 1, b). Esli zhe telo podletit eshe blizhe k Ch.d., to posle nesk. oborotov ili dazhe ne uspev sdelat' ni odnogo oborota, ono upadet v Ch.d.
|
| Ris. 2. |
|
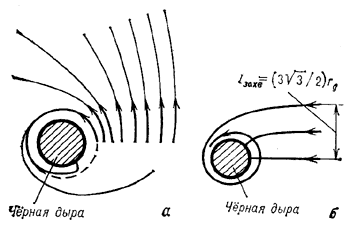
| Ris. 3. |
Nalichie kritich. okruzhnosti vedet k tomu, chto vse luchi s pricel'nym parametrom na
beskonechnosti ![]() gravitacionno zahvatyvayutsya
(ris. 3, b).
gravitacionno zahvatyvayutsya
(ris. 3, b).
3. Pole tyagoteniya vrashayusheisya chernoi dyry
Okolo vrashayusheisya Ch.d., kak uzhe bylo skazano, dolzhno sushestvovat' "vihrevoe" gravitac. pole. Vdali ot Ch.d. ono ochen' slabo, a vblizi vozrastaet nastol'ko, chto vedet k kachestvenno novym effektam.
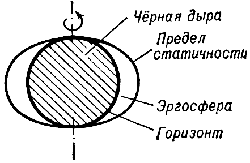
Tak, v okrestnosti vrashayusheisya Ch.d. voznikaet oblast', v k-roi vse tela i fotony uvlekatsya v dvizhenie vokurg Ch.d. Vnesh. granica etoi oblasti naz. predelom statichnosti. Odnako vnutri predela statichnosti tela i fotony sovsem ne obyazatel'no dolzhny padat' k centru, oni mogut i priblizhat'sya k Ch.d. i udalyat'sya ot nee, mogut vyhodit' za predel statichnosti. T.o., predel statichnosti ne yavl. granicei Ch.d., ee gorizontom, iz-pod k-rogo nel'zya vyiti. Lineinye razmery predela statichnosti po poryadku velichiny ravny rg. Gorizont Ch.d. raspolozhen glubzhe, pod predelom statichnosti. Prostranstvo mezhdu gorizontom i predelom statichnosti naz. ergosferoi (ris. 4). Predel statichnosti kasaetsya gorizonta v polyusah vrashayusheisya Ch.d.
Pri padenii tela na vrashayushuyusya Ch.d. ono snachala otklonyaetsya v svoem dvizhenii v storonu vrasheniya Ch.d., peresekaet granicu ergosfery i postepenno priblizhaetsya k gorizontu. Dlya vnesh. nablyudatelya svet, ispuskaemyi padayushim telom, stanovitsya vse bolee krasnym i menee intensivnym, zatem polnost'yu zatuhaet: telo, uidya pod gorizont, stanovitsya nevidimym dlya vnesh. nablyudatelya. Na gorizonte vse tela imeyut odnu tu zhe uglovuyu skorost' obrasheniya, v kakoe by mesto gorizonta ni popadalo padayushee telo.
Obshaya dlya vseh padayushih tel uglovaya skorost' ![]() na gorizonte Ch.d.
i est' skorost' ee vrasheniya:
na gorizonte Ch.d.
i est' skorost' ee vrasheniya: ![]() , gde I
-
moment impul'sa tela, iz k-rogo voznikla Ch.d.,
, gde I
-
moment impul'sa tela, iz k-rogo voznikla Ch.d., ![]() - massa,
S - ploshad' gorizonta Ch.d. Moment impul'sa Ch.d. zadannoi massy ne mozhet byt'
skol'
ugodno bol'shim. Maksimal'no vozmozhnye znacheniya I i
- massa,
S - ploshad' gorizonta Ch.d. Moment impul'sa Ch.d. zadannoi massy ne mozhet byt'
skol'
ugodno bol'shim. Maksimal'no vozmozhnye znacheniya I i ![]() opredelyayutsya tem, chto pri obrazovanii Ch.d. lineinaya skorost' vrasheniya tochek ekvatora
tela
ne prevyshaet skorosti sveta. Po poryadku velichiny
opredelyayutsya tem, chto pri obrazovanii Ch.d. lineinaya skorost' vrasheniya tochek ekvatora
tela
ne prevyshaet skorosti sveta. Po poryadku velichiny ![]() .
Dlya Ch.d. s massoi, ravnoi masse Solnca,
.
Dlya Ch.d. s massoi, ravnoi masse Solnca, ![]() (1/s).
(1/s).
|
| Ris. 4. |
Rassmotrim dlya primera zahvat fotona, dvizhushegosya v ploskosti ekvatora maksimal'no bystro vrashayusheisya Ch.d.
Dlya fotona, dvizhushegosya v napravlenii vrasheniya Ch.d., pricel'nyi parametr lzahv,1=1/2
rg; dlya fotona, dvizhushegosya
protiv vrasheniya, pricel'nyi parametr namnogo bol'she: lzahv,2=4
rg. Izmenyaetsya situaciya i s krugovymi orbitami.
Dlya Ch.d. bez vrasheniya poslednyaya ustoichivaya krugovaya orbita imeet radius 3rg;
chastica, dvizhushayasya po nei, imeet skorost' c/2. I samoe
vazhnoe: chtoby popast' na etu orbitu, chastica s massoi m dolzhna otdat' energiyu
![]() (energiyu svyazi) v vide, napr., gravitacionnogo
izlucheniya.
(energiyu svyazi) v vide, napr., gravitacionnogo
izlucheniya.
V sluchae maksimal'no bystro vrashayusheisya dyry poslednyaya krugovaya orbita lezhit v ekvatorial'noi
ploskosti blizko k gorizontu, gluboko vnutri ergosfery. No zdes' chastica mozhet
dvigat'sya tol'ko v storonu vrasheniya Ch.d. Energiya, k-ruyu vydelyaet chastica, popavshaya
na etu orbitu, gorazdo bol'she i sostavlyaet ![]() .
V to
zhe vremya poslednyaya ustoichivaya orbita chasticy, obrashayusheisya vokrug dyry v protivopolozhnom
napravlenii, lezhit vne ergosfery i chastica, popadayushaya v nee, vydelyaet energiyu
.
V to
zhe vremya poslednyaya ustoichivaya orbita chasticy, obrashayusheisya vokrug dyry v protivopolozhnom
napravlenii, lezhit vne ergosfery i chastica, popadayushaya v nee, vydelyaet energiyu ![]() .
.
Polnaya massa vrashayusheisya Ch.d. opredelyaetsya kak ee razmerami (ploshad'yu S gorizonta),
tak i energiei vrasheniya:
![]() .
.
Esli vrashenie otsutstvuet (I=0), to ![]() opredelyaetsya
tol'ko razmerami Ch.d. Pri maksimal'no vozmozhnoi skorosti vrasheniya Ch.d. vtoroe slagaemoe
pod kornem ravno pervomu.
opredelyaetsya
tol'ko razmerami Ch.d. Pri maksimal'no vozmozhnoi skorosti vrasheniya Ch.d. vtoroe slagaemoe
pod kornem ravno pervomu.
4. Fizicheskie processy v pole tyagoteniya chernoi dyry
V ergosfere Ch.d. vozmozhny processy, privodyashie k umen'sheniyu energii vrasheniya Ch.d.,
t.e., kak okazyvaetsya, Ch.d. mozhet teryat' energiyu. V chastnosti, kogda v ergosferu
vletae
chastica, imevshaya vdali ot Ch.d. energiyu ![]() (vklyuchaya energiyu
pokoya), i raspadaetsya na dve chasticy, to raspad mozhet proizoiti takim obrazom, chto
odna
chastica upadet na Ch.d., a drugaya, sravnitel'no nemnogo uvelichiv svoyu skorost' v moment
raspada, pereidet na takuyu orbitu, chto vyletit iz ergosfery s ogromnoi skorost'yu.
Eta
skorost' mozhet namnogo prevyshat' i pervonachal'nuyu skorost' podleta chasticy k ergosfere,
i velichinu izmeneniya skorosti pri raspade. V rezul'tate polnaya energiya vyletevshei
chasticy
(vklyuchaya energiyu
pokoya), i raspadaetsya na dve chasticy, to raspad mozhet proizoiti takim obrazom, chto
odna
chastica upadet na Ch.d., a drugaya, sravnitel'no nemnogo uvelichiv svoyu skorost' v moment
raspada, pereidet na takuyu orbitu, chto vyletit iz ergosfery s ogromnoi skorost'yu.
Eta
skorost' mozhet namnogo prevyshat' i pervonachal'nuyu skorost' podleta chasticy k ergosfere,
i velichinu izmeneniya skorosti pri raspade. V rezul'tate polnaya energiya vyletevshei
chasticy
![]() okazhetsya bol'she
okazhetsya bol'she ![]() . Izbytok energii
. Izbytok energii
![]() cherpaetsya iz energii vrasheniya Ch.d. Energiya
vrasheniya Ch.d. mozhet umen'shat'sya takzhe pri rasseyanii el.-magn. voln na Ch.d. Rasseyannaya
volna pri opredelennyh usloviyah mozhet okazat'sya intensivnee padayushei. Poterya energii
vrasheniya Ch.d. pri raspade chasticy v ergosfere dostigaet maksimuma, kogda raspad proishodit
na gorizonte. Pri etom ploshad' gorizonta ne menyaetsya. Vo vseh drugih sluchayah ploshad'
gorizonta neskol'ko uvelichivaetsya za schet energii chasticy, upavshei v Ch.d. Okazyvaetsya,
chto ploshad' gorizonta Ch.d. ne umen'shaetsya ni pri kakih processah voobshe (za isklyucheniem
medlennogo samoproizvol'nogo kvantovogo ispareniya Ch.d., o k-rom govoritsya dalee).
Napr., ch.d. mogut stolknut'sya i slit'sya v odnu. Chast' ih energii budet unesena pri
etom za
schet izlucheniya gravitac. voln, no gorizont voznikshei Ch.d. budet po ploshadi bol'she,
chem summa ploshadei gorizontov pervonachal'nyh dyr. Ni pri kakih vozdeistviyah (prilivnyh
i
drugih) Ch.d. ne mozhet razdelit'sya na dve ili bol'shee kolichestvo Ch.d.
cherpaetsya iz energii vrasheniya Ch.d. Energiya
vrasheniya Ch.d. mozhet umen'shat'sya takzhe pri rasseyanii el.-magn. voln na Ch.d. Rasseyannaya
volna pri opredelennyh usloviyah mozhet okazat'sya intensivnee padayushei. Poterya energii
vrasheniya Ch.d. pri raspade chasticy v ergosfere dostigaet maksimuma, kogda raspad proishodit
na gorizonte. Pri etom ploshad' gorizonta ne menyaetsya. Vo vseh drugih sluchayah ploshad'
gorizonta neskol'ko uvelichivaetsya za schet energii chasticy, upavshei v Ch.d. Okazyvaetsya,
chto ploshad' gorizonta Ch.d. ne umen'shaetsya ni pri kakih processah voobshe (za isklyucheniem
medlennogo samoproizvol'nogo kvantovogo ispareniya Ch.d., o k-rom govoritsya dalee).
Napr., ch.d. mogut stolknut'sya i slit'sya v odnu. Chast' ih energii budet unesena pri
etom za
schet izlucheniya gravitac. voln, no gorizont voznikshei Ch.d. budet po ploshadi bol'she,
chem summa ploshadei gorizontov pervonachal'nyh dyr. Ni pri kakih vozdeistviyah (prilivnyh
i
drugih) Ch.d. ne mozhet razdelit'sya na dve ili bol'shee kolichestvo Ch.d.
V ergosfere Ch.d. mogut protekat' kvantovye processy rozhdeniya chastic. V sil'nom pole tyagoteniya Ch.d. vakuum (predstavlyaet soboi fiz. polya v nainizshem energeticheskom sostoyanii) ne ustoichiv i iz nego mogut rozhdat'sya chasticy i antichasticy, v osnovnom bezmassovye: fotony, neitrino, gravitony.
Rozhdennye chasticy, uletaya iz ergesfery na beskonechnost', unosyat energiyu Ch.d. Harakternaya
chastota ![]() rozhdayushihsya fotonov po poryadku velichiny ravna
rozhdayushihsya fotonov po poryadku velichiny ravna ![]() .
Skorost' poteri energii vrasheniya Ch.d. opredelyaetsya sootnosheniem:
.
Skorost' poteri energii vrasheniya Ch.d. opredelyaetsya sootnosheniem:
![]() .
.
Chrezvychaino vazhno, chto vakuum neustoichiv v pole tyagoteniya ne tol'ko vrashayusheisya Ch.d.,
no i nevrashayusheisya. Eto oznachaet, chto za schet kvantovyh processov nevrashayushayasya Ch.d.
takzhe teryaet energiyu, umen'shayutsya ee massa i razmery. Nevrashayushayasya Ch.d. izluchaet
kak absolyutno chernoe telo s temp-roi T=1011(1015/![]() ) K, polnaya moshnost' el.-magn. izlucheniya L=1010(1015/
) K, polnaya moshnost' el.-magn. izlucheniya L=1010(1015/![]() ) erg/s, a vremya sushestvennogo
umen'sheniya massy Ch.d.
) erg/s, a vremya sushestvennogo
umen'sheniya massy Ch.d. ![]() let,
gde
let,
gde ![]() - znachenie massy Ch.d. v g. Privedennye sootnosheniya
pokazyvvayut,
chto kvantovye processy sovershenno nichtozhny dlya Ch.d., voznikshih iz zvezd s massami
- znachenie massy Ch.d. v g. Privedennye sootnosheniya
pokazyvvayut,
chto kvantovye processy sovershenno nichtozhny dlya Ch.d., voznikshih iz zvezd s massami
![]() >1034 g. Odnako oni sushestvenny
dlya
malomassivnyh pervichnyh Ch.d., k-rye mogli voznikat' na rannih etapah rasshireniya Vselennoi.
>1034 g. Odnako oni sushestvenny
dlya
malomassivnyh pervichnyh Ch.d., k-rye mogli voznikat' na rannih etapah rasshireniya Vselennoi.
Po mere umen'sheniya massy Ch.d. moshnost' izlucheniya dolzhna rasti, i v konce koncov malen'kaya Ch.d. porodit moshnuyu vspyshku zhestkogo gamma-izlucheniya (poslednie 109 g Ch.d. izluchaet za 0,1 s, chto podobno vzryvu milliona megatonnyh vodorodnyh bomb).
V real'nyh usloviyah Vselennoi ch.d., k-rye mogli vozniknut' iz zvezd, vse vremya uvelichivayut svoyu massu za schet padeniya na nih gaza i izlucheniya, v t.ch. i reliktovogo izlucheniya Vselennoi. Uvelichenie massy Ch.d. pri etom hotya obychno i malo, no sushestvenno prevyshaet poteri za schet kvantovogo ispareniya.
Ch.d., voznikshie v rezul'tate kollapsa massivnyh zvezd, mogut vyzyvat' svoim sil'nym gravitac. polem burnye processy pri padenii v nih gaza. Takie gazovye potoki mogut byt' osobenno moshnymi, kogda na Ch.d., vhodyashuyu v sostav tesnoi dvoinoi zvezdnoi sistemy, gaz peretekaet ot zvezdy-giganta. Gaz, nagretyi pri padenii v pole tyagoteniya Ch.d., daet rentg. izluchenie, i po etomu izlucheniyu Ch.d. mozhet byt' obnaruzhena. Veroyatno, odna ch.d. uzhe obnaruzhena takim sposobom v rentg. istochnike Lebed' H-1 (sm. Rentgenovskaya astronomiya, Akkrecionnye diski).
Vozmozhno, chto v centre yader galaktik i kvazarov sushestvuyut sverhmassivnye Ch.d., s
massoi do ![]() , v pole tyagoteniya k-ryh protekayut
burnye
processy, yavlyayushiesya prichinoi aktivnosti yader galaktik i kvazarov.
, v pole tyagoteniya k-ryh protekayut
burnye
processy, yavlyayushiesya prichinoi aktivnosti yader galaktik i kvazarov.
Lit.:
Zel'dovich Ya.B., Novikov I.D., Teoriya tyagoteniya i evolyuciya zvezd, M., 1971; Mizner
Ch., Torn K., Uiler Dzh., Gravitaciya, t. 3, per. s angl., M., 1977; Frolov V.P., Chernye
dyry
i kvantovye processy v nih, UFN, 1976, t. 118, v. 3, s. 473; Torn K., Poiski chernyh
dyr, per. s angl., tam zhe, s. 453.
(I.D. Novikov)
|
Publikacii s klyuchevymi slovami:
chernye dyry - black hole
Publikacii so slovami: chernye dyry - black hole | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |