Astronet > Chandrasekara predel

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Na saite

Astrometriya

Astronomicheskie instrumenty

Astronomicheskoe obrazovanie

Astrofizika

Istoriya astronomii

Kosmonavtika, issledovanie kosmosa

Lyubitel'skaya astronomiya

Planety i Solnechnaya sistema

Solnce

Chandrasekara predel

verhnii predel massy ${\mathfrak M}_Ch$ holodnogo nevrashayushegosya belogo karlika. Ustanovlen S. Chandrasekarom (SShA) v 1931 g. Davlenie p vnutri belogo karlika (B.k.) opredelyaetsya elektronnym vyrozhdennym gazom i zavisit tol'ko ot plotnosti veshestva $\rho$ . S uvelicheniem $\rho$ elektronnyi gaz stanovitsya relyativistskim, i eta zavisimost' asimptoticheski priblizhaetsya k zakonu
$p=K\rho^{4/3}$ , (1)
gde
$K={1\over 8} \left({3\over {\pi}} \right)^{1/3} {hc\over {(m_u\mu_e)^{4/3}}} \approx {1,244\cdot 10^{15}\over {\mu_e^{4/3}}} \left[ {sm^3\over {s^2\cdot g^{1/3}}} \right]$ . (2)

Zdes' m_u atomnaya edinica massy, $\mu_e$ - molekulyarnaya massa, prihodyashayasya na odin elektron [chislo elektronov v ed. ob'ema ravno $\rho/(m_u\mu_e)$ ]. Chem bol'she massa ${\mathfrak M}$ B.k., tem tochnee vypolnyaetsya sootnoshenie (1) i tem luchshe stroenie B.k. sootvetstvuet modeli politropnogo shara. Teoriya politropnyh gazovyh sharov - gidrostaticheski ravnovesnyh sfericheski-simmetrichnyh konfiguracii, vnutri k-ryh $p\sim\rho^{1+{1\over n}}$ [sluchayu (1) sootvetstvuet n=3], - byla razvita v konce 19 - nachale 20 vv. Dzh. Leinom (SShA), A. Ritterom (Germaniya) i R. Emdenom (Shveicariya). Soglasno etoi teorii, v sluchae n=3 imeetsya odnoznachnaya svyaz' mezhdu postoyannoi K i massoi ${\mathfrak M}$ politropnogo shara:
$K=0,3639\cdot G{\mathfrak M}^{2/3}$ , (3)
gde 0,3639 - koefficient, opredelyaemyi usloviem gidrostatich. ravnovesiyayu Podstavlyaya znachenie K iz (2) v (3), poluchaem predel'nuyu massu ${\mathfrak M}_Ch$ B.k.
${\mathfrak M}_Ch={0,1967\over {(m_u\mu_e)^2}} \left( {hc\over G} \right)^{3/2} = {5,83\over {\mu_e^2}} {\mathfrak M}_\odot$ . (4)
Kogda massa ${\mathfrak M}$ B.k. priblizhaetsya k ${\mathfrak M}_Ch$ snizu, plotnost' veshestva vnutri B.k. neogranichenno vozrastaet i svyaz' mezhdu davleniem i plotnost'yu vse tochnee opisyvaetsya sootnosheniem (1). Pri etom radius B.k. stremitsya k nulyu. Pri ${\mathfrak M}>{\mathfrak M}_Ch$ gidrostatich. ravnovesie B.k. voobshe nevozmozhno, poskol'ku gradient davleniya nedostatochen dlya kompensacii sily tyazhesti. V tabl. dlya razlichnyh veshestv privedeny okruglennye znacheniya $\mu_e$ i sootvetstvuyushie ${\mathfrak M}_Ch$ :

¹H ⁴He, ¹²C, ¹⁴N, ¹⁶O, ²⁰Ne, ²⁴Mg, ²⁸Si, ⁴⁰Ca,... -
v chistom vide ili smeshannye
v lyuboi proporcii ⁵²Cr ⁵⁶Fe ⁵⁹Co ⁵⁸Ni

$\mu_e$ 1,01 2,00 2,16 2,15 2,18 2,07

${{\mathfrak M}_Ch\over{{\mathfrak M}_\odot}}$ 5,73 1,46 1,24 1,26 1,22 1,36

Pri dostatochno bol'shih plotnostyah na strukturu real'nyh B.k. nachinayut zametno vliyat' processy neitronizacii veshestva i effekty obshei teorii otnositel'nosti. V rezul'tate maks. massa ${\mathfrak M}_{maks}$ B.k. okazyvaetsya neskol'ko men'she ${\mathfrak M}_Ch$ i ei sootvetstvuet uzhe ne beskonechnaya, a konechnaya velichina central'noi plotnosti $\rho_s$ (ris.). Tak, dlya uglerodnyh B.k. s uchetom etih faktorov ${\mathfrak M}_{maks}\approx 1,36 {\mathfrak M}_\odot$ i $\rho_{maks}\approx 5\cdot 10^{10}$ g/sm³, chemu sootvetstvuet minimal'nyi radius B.k. ~ 10⁸ sm, t.e. 1 tys. km.

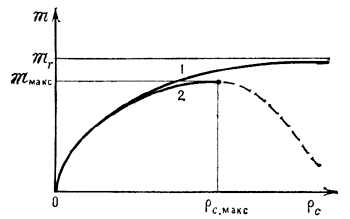
Kachestvennyi vid zavisimosti massy belyh karlikov
ot ih central'noi plotnosti.
1 - ideal'nye belye karliki, dlya k-ryh $\rho_c\to\infty$
pri ${\mathfrak M}\to {\mathfrak M}_Ch$ ;
2 - real'nye belye karliki: maksimal'noi masse ${\mathfrak M}_{maks}$
sootvetstvuet konechnaya
central'naya plotnost' $\rho_{c,maks}$ .
Shtrihovoi otrezok krivoi sootvetstvet neustoichivym konfiguraciyam.

Dostatochno goryachie B.k., elektronnyi gaz vnutri k-ryh vyrozhden ne polnost'yu, a takzhe holodnye, no bystro vrashayushiesya B.k. mogut imet' massy, prevyshayushie ${\mathfrak M}_Ch$ . So vremenem po mere ohlazhdeniya i (ili) poteri momenta kolichestva dvizheniya gidrostatich. ravnovesie takih massivnyh B.k. neminuemo narushaetsya i oni perehodyat v sostoyanie gravitacionnogo kollapsa , v rezul'tate chego voznikaet neitronnaya zvezda.

Ch.p. igraet fundamental'nuyu rol' v teorii stroeniya i evolyucii zvezd. Vnutri massivnyh zvezd na opredelennyh stadiyah evolyucii mogut obrazovyvat'sya chastichno vyrozhdennye central'nye yadra, sostoyashie iz C, O, Ne, Si, Fe. Harakter posleduyushih, zaklyuchitel'nyh stadii evolyucii takih zvezd, a takzhe ih konechnaya sud'ba kriticheski zavisyat ot togo, naskol'ko i v kakuyu storonu otlichayutsya massy ih yader ot ${\mathfrak M}_Ch$ .

(D.K. Nadezhin)

D. K. Nadezhin, "Fizika Kosmosa", 1986
Glossarii Astronet.ru

A | B | V | G | D | Z | I | K | L | M | N | O | P | R | S | T | U | F | H | C | Ch | Sh | E | Ya

Publikacii s klyuchevymi slovami: predel Chandrasekara - Chandrasekarovskaya massa Publikacii so slovami: predel Chandrasekara - Chandrasekarovskaya massa
Sm. takzhe: Rassvet pered vzryvom novoi zvezdy Belye karliki Subrahman'yan Chandrasekar (1910-1995 gg.) Predel, Chandrasekara

Obsudit' etu publikaciyu

Versiya dlya pechati

	¹H	⁴He, ¹²C, ¹⁴N, ¹⁶O, ²⁰Ne, ²⁴Mg, ²⁸Si, ⁴⁰Ca,... - v chistom vide ili smeshannye v lyuboi proporcii	⁵²Cr	⁵⁶Fe	⁵⁹Co	⁵⁸Ni
$\mu_e$	1,01	2,00	2,16	2,15	2,18	2,07
${{\mathfrak M}_Ch\over{{\mathfrak M}_\odot}}$	5,73	1,46	1,24	1,26	1,22	1,36