Astronet > Elementy orbity

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Elementy orbity

- velichiny, harakterizuyushie orbitu nebesnogo tela, a takzhe polozheniya tela na orbite.

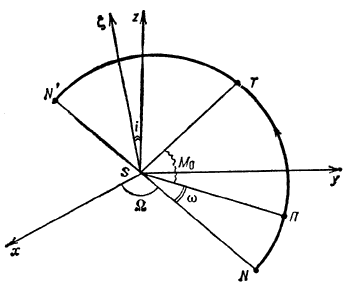
Ris. 1

Orbita nebesnogo tela, dvizhushegosya v pole tyagoteniya dr. tela, predstavlyaet soboi krivuyu vtorogo poryadka (konich. sechenie), v odnom iz fokusov k-roi nahoditsya centr mass dvuh tel (prityagivayushii centr). Dannoe opredelenie otnositsya k sluchayu, kogda vzaimodeistvuyushie tela sfericheski-simmetrichny ili zhe nahodyatsya na stol' bol'shom rasstoyanii, chto otklonenie ih formy ot sfericheskoi ne skazyvaetsya sushestvenno na sile vzaimodeistviya.

Tochka orbity tela, blizhaishaya k prityagivayushemu centru, naz. pericentrom, a naibolee udalennaya - apocentrom. Esli prityagivayushim centrom yavl. Zemlya, to eti tochki naz. perigeem i apogeem; dlya Solnca - perigeliem i afeliem, dlya proizvol'noi zvezdy - periastrom i apoastrom. Pryamaya, soedinyayushaya apocentr i pericentr, nosit nazvanie linii apsid.

Elementy, harakterizuyushie polozhenie ploskosti orbity i orientaciyu orbity v zhtoi ploskosti, vvodyatsya sled. obrazom.

Na ris. 1 S^xy - osn. koordinatnaya ploskost'. Za osn. koordinatnuyu ploskost' v raznyh zadachah vybirayut razlichnye ploskosti: v zvezdnoi astronomii - eto ploskost' Galaktiki, v teorii dvizheniya ISZ - eto ploskost' zemnogo ekvatora.

Os' S^x napravlena v osnovnuyu tochku, za k-ruyu dlya orbit tel v Solnechnoi sisteme chashe vsego prinimayut tochku vesennego ravnodenstviya $\Upsilon$ (odnu iz tochek peresecheniya ekvatora s ekliptikoi). Ploskost' NPN' - ploskost' orbity nebesnogo tela, P - pericentr orbity, $\zeta$ - polyus orbity (on nahoditsya na pryamoi, prohodyashei cherez tyagoteyushii centr i perpendikulyarnoi k ploskosti orbity), T - polozhenie nebesnogo tela na orbite.

Pryamaya NSN', po k-roi ploskost' orbity NPN' peresekaetsya s osn. koordinatnoi ploskost'yu S^xy, naz. liniei uzlov. Polupryamaya SN, k-ruyu nebesnoe telo peresekaet, perehodya iz oblasti z <0 v oblast' z >0, pokazyvaet polozhit. napravlenie linii uzlov. Esli dvizhenie nebesnogo tela proisodit protiv chasovoi strelki dlya nablyudatelya, nahodyashegosya v polyuse orbity $\zeta$ , to tochka N naz. voshodyashim uzlom orbity, a N' - nishodyashim uzlom. Ugol $\Omega$ mezhdu os'yu S^x i polupryamoi SN naz. dolgotoi voshodyashego uzla. Etot ugol otschityvaetsya ot osi S^x v storonu osi S^y ot 0 do 360^o. Ugol i mezhdu ploskost'yu orbity i ploskost'yu S^xy naz. naklonom orbity. Naklon mozhet imet' vse znacheniya ot 0 do 180^o. Esli $0^\circ\le i <90^\circ$ , to dvizhenie naz. pryamym, esli zhe $90^\circ < i \le 180^\circ$ , to obratnym. Uglovoe rasstoyanie $\omega$ linii apsid SP ot linii uzlov SN naz. rasstoyaniem pericentra ot uzla ili argumentom pericentra. Ugol $\omega$ otschityvaetsya v napravlenii dvizheniya tela ot 0 do 360^o. Polozhenie linii apsid inogda opredelyayut otnositel'no napravleniya S^x. Dlya etogo vvodyat ugol $\pi$ - dolgotu pericentra. Ugol $\pi$ otschityvaetsya ot napravleniya S^x v ploskosti xS^y do linii uzolov SN i dalee v ploskosti orbity do linii apsid SP, inache $\pi=\Omega+\omega$ .

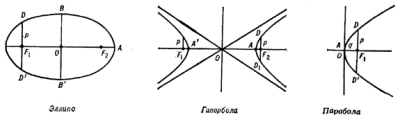
Ris. 2

Velichiny $\Omega, i, \omega$ sostavlyayut pervuyu gruppu elementov orbity, pervye dlya iz nih harakterizuyut polozhenie ploskosti orbity, a tretii - orientaciyu orbity v etoi ploskosti.

Razmer orbity i ee formu harakterizuyut elementy p i e - parametr i ekscetresitet (ris. 2). Ekscetresitetom orbity e naz. otnoshenie rasstoyaniya mezhdu fokusami F¹F²=2c etoi orbity k rasstoyaniyu mezhdu ee vershinami A i A'. Rasstoyanie mezhdu ee vershinami oboznachayut 2a, a velichinu a naz. bol'shoi poluos'yu orbity, tak chto e=c/a. Dlya paraboly c=a, poetomu e=1. Dlya ellipsa e <1, dlya giperboly e >1. Polovina fokal'noi hordy DD' orbity, perpendikulyarnoi k ee osi, nosit nazvanie fokal'nogo parametra i oboznachaetsya bukvoi p. Vmesto dvuh elementov p i e dlya paraboly ispol'zuyut odin element q=p/2 - perigeliinoe rasstoyanie (na ris. 2 otrezok AF¹). Dvizhenie po krugovoi orbite yavl. chastnym sluchaem dvizheniya po ellipsu (e=0). Ekscetresitetom orbity e inogda zamenyayut uglom ekscetresiteta $\varphi$ , opredelyaemym f-loi $e=\sin\varphi$ . Polozhenie nebesnogo tela na orbite v nek-ryi nachal'nyi moment vremeni t⁰ opredelyaetsya ego uglovym rasstoyaniem ot linii apsid. Etot ugol oboznachaetsya cherez M⁰ i naz. srednei anomaliei v epohu. Chasto v kachetve elementa vybirayut moment vremeni $\tau$ prohozhdeniya nebesnogo tela cherez pericentr orbity. Elementy M⁰ i $\tau$ svyazany mezhdu soboi sootnosheniem $M_0=n(t_0-\tau)$ , gde n - srednee dvizhenie nebesnogo tela. Element n inogda upotreblyayut vmesto elementa a.

Elementy $p, e, i, \Omega, \omega, \tau$ naz. keplerovskimi elementami. Oni opredelyayut orbitu nezavisimo ot togo, yavl. li ona ellipticheskoi, giperbolicheskoi ili parabolicheskoi.

Skorost' krugovogo dvizheniya (pervaya kosmicheskaya skorost') opredelyaetsya f-loi $v_K=\sqrt{\mu/r}$ , gde $\mu$ - proizvedenie gravitac. postoyannoi na summu mass prityagivayushih tel, r - rasstoyanie mezhdu ih centrami mass. Pri v^K < v < v^P dvizhenie proishodit po ellipsu. Pri $v=v_P=\sqrt{2\mu/r}$ ellips razryvaetsya i telo dvizhetsya po parabolicheskoi traektorii. Skorost' v^P naz. skorost'yu otryva ot prityagivayushego centra ili vtoroi kosmicheskoi skorost'yu. Pri v > v^P nebesnoe telo dvizhetsya po giperbole.

(S.N. Vashkov'yak)

S. N. Vashkov'yak, "Fizika Kosmosa", 1986
Glossarii Astronet.ru

L | R | A | B | V | G | D | E | Zh | Z | I | ' | K | L | M | N | O | P | R | S | T | U | F | H | C | Ch | Sh | Sh | E | Yu | Ya

Publikacii s klyuchevymi slovami: elementy orbity Publikacii so slovami: elementy orbity
Sm. takzhe: Dvoinaya zvezda Micar

Obsudit' etu publikaciyu

Versiya dlya pechati