Astronet > Komptonovskoe rasseyanie

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Komptonovskoe rasseyanie

- uprugoe rasseyanie fotona na svobodnom elektrone. K. r. opredelyaet neprozrachnost' veshestva dlya zhestkih (vysokoenergichnyh) rentgenovskih i gamma-luchei. Ono igraet vazhnuyu rol' v atmosferah neitronnyh zvezd, v rentg. istochnikah, v nedrah zvezd. Chastnym sluchaem K. r. v predele nizkochastotnyh fotonov i maloenergichnyh elektronov yavl. tomsonovskoe rasseyanie. Rasseyanie fotona na pokoyashemsya elektrone v silu zakonov sohraneniya energii i kolichestva dvizheniya soprovozhdaetsya umen'sheniem energii fotona i peredachei ee elektronu. Eto yavlenie bylo eksperimental'no otkryto v 1922 g. amer. fizikom A. Komptonom, issledovavshim rasseyanie rentg. luchei v grafite, i izvestno kak effekt Komptona (kompton-effekt), ili effekt otdachi. Rasseyanie nizkochastotnyh fotonov na ul'trarelyativistskih elektronah privodit k uvelicheniyu (vo mnogo raz) energii fotonov - t.n. obratnyi kompton-effekt. Obratnyi kompton-effekt yavl. odnim iz vazhneishih mehanizmov formirovaniya spektrov rentgenovskogo i gamma-izlucheniya astronomich. ob'ektov.

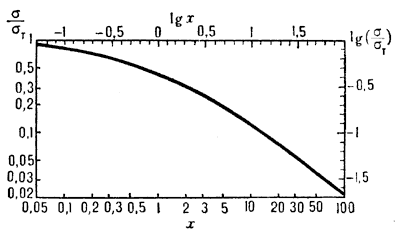
Ris. 1. Zavisimost' secheniya komptonovskogo
rasseyaniya $\sigma$ ot parametra
$x=(2h\nu/m_ec^2)\cdot \gamma(1-\mu v/c)$ .
Sechenie normirovano na $\sigma_T$ .

Sechenie K. r. (sechenie Kleina-Nishiny-Tamma) zavisit ot parametra $x=(2h\nu/m_ec^2)\cdot \gamma(1-\mu v/c)$ , gde $\nu$ - chastota fotona do rasseyaniya, ( $\mu$ - kosinus ugla $\Theta$ mezhdu napravleniyami rasprostraneniya fotona i elektrona do rasseyaniya, v - skorost' elektrona do rasseyaniya, $\gamma=[1-(v/c)^2]^{-1/2}$ - lorenc-faktor elektrona. Eta zavisimost' privedena na ris. 1. V sluchae rasseyaniya na pokoyashemsya elektrone $x=2h\nu/m_ec^2$ . V nerelyativistskom predele (pri $x\ll 1$ ) sechenie $\sigma$ medlenno umen'shaetsya: $\sigma=\sigma_T(1-x)$ . V ul'trarelyativistskom predele ( $x\gg 1$ ) ono bystro ubyvaet s rostom h: $\sigma=(3/4)\sigma_T\cdot x^{-1}(\ln x+1/2)$ . T. o., dlya nizkochastotnyh fotonov sechenie rasseyaniya ravno secheniyu tomsonovskogo rasseyaniya $\sigma_T=(8\pi/3)(e^2/m_ec^2)= 6,65\cdot 10^{-25} \mbox{sm}^2$ . Pri rasseyanii na pokoyashihsya elektronah indikatrisa rasseyaniya nizkochastotnyh fotonov releevskaya (sm. Releevskoe rasseyanie). Pri $h\nu\ge m_ec^2$ uvelichivaetsya veroyatnost' rasseyaniya vpered, t.e. v napravlenii rasprostraneniya fotona (sm. ris. 1 v st. Vzaimodeistvie izlucheniya s veshestvom).

Kak i tomsonovskoe rasseyanie, K. r. mozhet privodit' k zametnym polyarizac. effektam.

V processe K. r. izmenyayutsya chastota fotona i energiya elektrona. Chastota fotona posle rasseyaniya
$\nu'=\nu\;{1-\mu {v\over c}\over {1-\mu'{v\over c} + {h\nu\over {\gamma m_ec^2}}(1-\cos\alpha)}}$ , (1)
gde $\mu'$ - kosinus ugla $\Theta'$ mezhdu napravleniyami rasprostraneniya fotona posle rasseyaniya i elektrona do rasseyaniya, $\alpha$ - ugol rasseyaniya (ugol mezhdu napravleniyami rasprostraneniya fotona do i oposle rasseyaniya, ris. 2). Pri rasseyanii na pokoyashemsya elektrone (effekt Komptona)
$\nu'=\nu\;{1\over {1 + {h\nu\over {m_ec^2}}(1-\cos\alpha)}}$
ili
$\lambda'=\lambda + {h\over {m_ec}}(1-\cos\alpha)$ , (2)
t. e. dlina volny fotona $\lambda$ pri rasseyanii uvelichivaetsya, eto uvelichenie (proporcional'noe h i, sledovatel'no, imeyushee kvantovuyu prirodu) zavisit lish' ot ugla rasseyaniya. Velichina $$\lambda_C=h/m_ec=0,024 $\AA$ naz. komptonovskoi dlinoi volny. Iz (2) vidno, chto izmenenie dliny volny fotona pri rasseyanii na nepodvizhnom elektrone ne prevyshaet $\lambda$ i, t.o., sushestvenno lish' dlya dostatochno korotkovolnovogo izlucheniya.

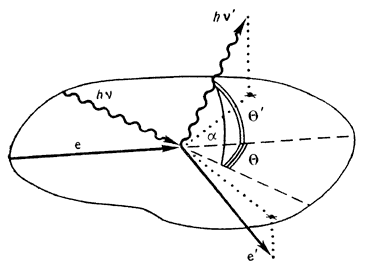
Ris. 2. Geometriya komptonovskogo rasseyaniya.
Sploshnye strelki - napravleniya dvizheniya
elektrona do i posle rasseyaniya,
volnistye - to zhe dlya fotona.

Pri K. r. zhestkogo fotona $\gamma_1$ s energiei $h\nu_1$ na elektrone imeetsya malaya veroyatnost' rozhdeniya nizkochastotnogo fotona $\gamma_2$ s energiei $h\nu_2 < h\nu_1$ : $\gamma_1+{\rm e \to e} +\gamma_1+\gamma_2$ . Etot process naz. dvoinym kompton-effektom. Rozhdenie nizkochastotnyh fotonov vsledstvie dvoinogo kompton-effekta mozhet konkurirovat' s tormoznym processom e+p $\to$ e+p+ $\gamma_t$ (sm. Tormoznoe izluchenie) lish' v ekstremal'no razrezhennoi i goryachei plazme na rannih stadiyah rasshireniya Vselennoi, v rentgenovskih i gamma-istochnikah.

Kompton-effekt ogranichivaet probeg zhestkih fotonov v veshestve. V rezul'tate mnogokratnyh rasseyanii zhestkii foton umen'shaet svoyu energiyu (otdavaya ee elektronam), perehodit v dr. oblast' spektra i pogloshaetsya vsledstvie fotoionizacii atomov. K. r. opredelyaet dlinu probega zhestkih rentg. fotonov (10 keV < $h\nu$ < 3 MeV) v razrezhennoi astrofizich. plazme. Rasseyanie zhestkih fotonov s $h\nu > 3$ keV na elektrone v atome vodoroda (ili dr. atoma) proishodit s tem zhe secheniem, chto i na svobodnom elektrone. Eto svyazano s tem, chto energiya, soobshaemaya elektronu v silu effekta otdachi, prevyshaet energiyu svyazi elektrona v atome vodoroda.

Pri rasseyanii nizkochastotnyh fotonov na ul'trarelyativistskih elektronah (obratnyi kompton-effekt) maksimal'na veroyatnost' rasseyaniya fotonov v napravlenii dvizheniya elektrona ( $\mu'\sim 1$ ). Esli $h\nu/\gamma m_ec^2\ll 1$ to, kak sleduet iz (1), izmenenie chastoty fotona opisyvaetsya f-loi:
$\nu'=\nu\;{1-\mu {v\over c}\over {1-\mu'{v\over c}}}$ . (3)
T. o., pri rasseyanii nizkochastotnyh fotonov na ul'trarelyativistskih elektronah izmenenie chastoty proishodit tol'ko iz-za Doplera effekta (tak zhe, kak pri otrazhenii ot dvizhusheisya stenki), a sechenie rasseyaniya ravno tomsonovskomu (mala velichina h). Eto legko ponyat', poskol'ku v etom sluchae v sisteme pokoya elektrona proishodit klassich. tomsonovskoe rasseyanie. Sledovatel'no, obratnyi kompton-effekt, v otlichie ot kompton-effekta, yavl. chisto klassich. effektom (izmenenie chastoty ne zavisit ot h). Iz (3) takzhe sleduet, chto pri rasseyanii v napravlenii dvizheniya elektrona ( $\mu'\sim 1$ ) proishodit znachit. uvelichenie chastoty fotona $\nu\sim\gamma^2\nu$ . Chastota fotonov pri rasseyanii na izotropno raspredelennyh relyativistskih elektronah v srednem dolzhna uvelichivat'sya v $(4/3)\gamma^2$ raz. Takoe zhe sr. uvelichenie imeet mesto, esli fotony izotropnogo polya izlucheniya rasseivayutsya na puchke ul'trarelyativistskih elektronov. Esli elektrony imeyut stepennoe raspredelenie po energiyam $dN_e=K\varepsilon_e^{-\beta}\;d\varepsilon_e$ (dN_e - koncentraciya relyativistskih elektronov v intervale energii ot $\varepsilon_e$ , do $\varepsilon_e+d\varepsilon_e$ , to spektr zhestkogo izlucheniya, formiruyushegosya v rezul'tate obratnogo kompton-effekta nizkochastotnyh fotonov, takzhe okazyvaetsya stepennym. Ego intensivnost' $I_\nu=B\nu^{-s}$ (K i B - konstanty), gde spektr. indeks $s=(\beta-1)/2$ . Pri ochen' vysokih energiyah elektronov, kogda parametr h stanovitsya bol'shim, umen'shaetsya sechenie rasseyaniya, prirost energii fotonov pri rasseyanii stanovitsya men'she, chem $\sim\gamma^2\nu$ . Eto privodit k otkloneniyu spektra zhestkogo izlucheniya ot stepennogo zakona. Asimptoticheski intensivnost' $I_\nu\sim\nu^{-\beta}\ln(h\nu kT_r/m_e^2c^4)$ , gde T_r - temp-ra nizkochastotnyh fotonov.

Obratnyi kompton-effekt chasto schitayut osn. mehanizmom formirovaniya zhestkih stepennyh spektrov izlucheniya v kvazarah i yadrah galaktik. Etot process yavl. osn. prichinoi poter' energii relyativistskimi elektronami v izotropnom pole nizkochastotnogo izlucheniya (napr., v pole mikrovolnovogo fonovogo izlucheniya, zapolnyayushego Vselennuyu) ili v pole izlucheniya kompaktnyh ob'ektov. Harakternoe vremya poter' energii v takom pole izlucheniya $t\approx (3/4)m_e c/\sigma_T \varepsilon_r \gamma$ , t.e. tem men'she, chem vyshe energiya elektrona ( $\sim\gamma$ ) i plotnost' energii izlucheniya $\varepsilon_r$ . Pri $\varepsilon_r>H^2/8\pi$ , gde N - napryazhennost' magn. polya, poteri energii na obratnyi kompton-effekt prevyshayut poteri na sinhrotronnoe izluchenie.

K. r. mozhet proishodit' ne tol'ko na elektronah, no i na lyubyh dr. zaryazhennyh chasticah (napr., protonah). No poskol'ku sechenie K. r. obratno proporcional'no kvadratu massy, K. r. na tyazhelyh chasticah sushestvenno menee effektivno.

(R.A. Syunyaev)

R. A. Syunyaev, "Fizika Kosmosa", 1986
Glossarii Astronet.ru

L | R | A | B | V | G | D | E | Zh | Z | I | ' | K | L | M | N | O | P | R | S | T | U | F | H | C | Ch | Sh | Sh | E | Yu | Ya

Publikacii s klyuchevymi slovami: komptonovskoe rasseyanie - kompton-effekt Publikacii so slovami: komptonovskoe rasseyanie - kompton-effekt
Sm. takzhe: Novoe otkrytie "Planka". Komptonizaciya

Obsudit' etu publikaciyu

Versiya dlya pechati