Astronet > Keplera zakony

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Keplera zakony

- tri zakona dvizheniya planet otnositel'no Solnca, ustanovlennye empiricheski nem. astronomom I. Keplerom v nachale 17 v.

1-i zakon:
kazhdaya planeta dvizhetsya po ellipsu, v odnom iz fokusov k-rogo nahoditsya Solnce.
2-i zakon:
kazhdaya planeta dvizhetsya v ploskosti, prohodyashei cherez centr Solnca, prichem ploshad' sektora orbity, opisannaya radiusom-vektorom planety, izmenyaetsya proporcional'no vremeni. Chasto 2-i zakon formuliruyut kak zakon ploshadei: radius-vektor planety v ravnye promezhutki vremeni opisyvaet ravnye ploshadi (ris.).
3-i zakon:
kvadraty periodov obrasheniya planet vokrug Solnca otnosyatsya kak kuby ih sr. rasstoyanii ot Solnca. Esli oboznachit' periody obrasheniya dvuh planet cherez T₁ i T₂, a ih sr. rasstoyaniya ot Solnca (bol'shie poluosi ih orbit) cherez a₁ i a₂, to 3-i K. z. mozhno zapisat' v vide: $T_1^2/T_2^2=a_1^3/a_2^3$ . K. z. sygrali bol'shuyu rol' v ustanovlenii I. N'yutonom zakona vsemirnogo tyagoteniya, oni voshli v nebesnuyu mehaniku v obobshennoi i utochnennoi forme, v etoi forme oni primenyayutsya pri issledovanii orbit, opisyvaemyh dvumya gravitacionno svyazannymi nebesnymi telami pri otsutstvii vozmushenii so storony dr. tel (v t.n. zadache dvuh tel). Pod deistviem prityazheniya Solnca razlichnye tela (planety, asteroidy, komety, KA) v zavisimosti ot svoei skorosti (tochnee, polnoi mehanich. energii) mogut dvigat'sya kak po zamknutym traektoriyam (okruzhnostyam i ellipsam), tak i po razomknutym traektoriyam (parabolam i giperbolam). Vse perechislennye vidy traektorii predstavlyayut soboi t.n. konich. secheniya.

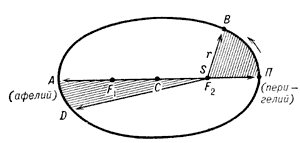
Orbita planety Solnechnoi sistemy PVADP -
ellips; F₁ i F₂ - fokusy ellipsa,
v odnom iz fokusov nahoditsya Solnce S;
SP=SA - bol'shaya poluos' orbity; r -
radius-vektor planety; planeta prohodit
otrezki traektorii PV i AD za odinakovoe
vremya, ploshadi sektorov SPV i SAD ravny.

Obobshennaya formulirovka 1-go K. z. takova: traektoriya tela, dvizhushegosya v pole tyagoteniya Solnca, predstavlyaet soboi konich. sechenie, v odnom iz fokusov k-rogo nahoditsya Solnce. 2-i K. z. yavl. sledstviem central'nogo haraktera sil tyagoteniya, deistvuyushih mezhdu Solncem i dvizhushimsya telom. V differencial'nye ur-niya otnositel'nogo dvizheniya dvuh prityagivayushihsya tel vhodit summa ih mass, i eta summa poyavlyaetsya v utochnennoi N'yutonom formulirovke 2-go K. z.: kvadraty periodov obrasheniya tel vokrug Solnca, umnozhennye na summu mass kazhdogo tela i Solnca, otnosyatsya kak kuby bol'shih poluosei orbit: ${T_1^2({\mathfrak M}_1+{\mathfrak M}_\odot)\over {T_2^2({\mathfrak M}_2+{\mathfrak M}_\odot)}}={a_1^3\over {a_2^3}}$ , gde ${\mathfrak M}_\odot$ - massa Solnca, ${\mathfrak M}_1$ i ${\mathfrak M}_2$ - massy rassmatrivaemyh tel (planet).

V pervom priblizhenii mozhno prenebrech' massami planet (a tem bolee massami malyh tel Solnechnoi sistemy) sravnitel'no s massoi Solnca i togda budet imet' mesto formulirovka 3-go zakona, dannaya Keplerom.

Usloviem dvizheniya tel po zamknutym elliptich. traektoriyam vokrug Solnca yavl. otricat. znachenie polnoi mehanich. energii tela v Solnechnoi sisteme; usloviem dvizheniya po razomknutoi traektorii i, sledovatel'no, razryva dinamich. svyazi tela s Solncem - polozhit. znachenie mehanich. energii tela. Giperbolich. dvizhenie mozhet pereiti v ellipticheskoe tol'ko v sluchae umen'sheniya po k.-l. prichine (napr., vliyaniya tret'ego tela) polnoi energii dvizhushegosya tela do otricatel'nogo znacheniya (zahvat dvizhushegosya tela).

"Fizika Kosmosa", 1986
Glossarii Astronet.ru

L | R | A | B | V | G | D | E | Zh | Z | I | ' | K | L | M | N | O | P | R | S | T | U | F | H | C | Ch | Sh | Sh | E | Yu | Ya

Mneniya chitatelei [4]

Versiya dlya pechati

Publikacii s klyuchevymi slovami: zakony Keplera - pervyi zakon Keplera - vtoroi zakon Keplera - tretii zakon Keplera - Nebesnaya mehanika - zadacha dvuh tel Publikacii so slovami: zakony Keplera - pervyi zakon Keplera - vtoroi zakon Keplera - tretii zakon Keplera - Nebesnaya mehanika - zadacha dvuh tel
Sm. takzhe: Saimon N'yukom (1835 -1909) k 175-letiyu so dnya rozhdeniya. Naum Il'ich Idel'son - 125 let so dnya rozhdeniya Kak Kepler otkryvaet zakony dvizheniya planet Metody teorii special'nyh vozmushenii v nebesnoi mehanike Zadacha N tel i problema integriruemosti K 90-letiyu Aleksandra Aleksandrovicha Orlova Dinamika zvezdnyh skoplenii Vse publikacii na tu zhe temu >>