Astronet > Lineichatoe izluchenie (izluchenie v liniyah)

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Lineichatoe izluchenie (izluchenie v liniyah)

1. Vvedenie
2. Lokal'noe termodinamicheskoe ravnovesie
3. Koronal'nyi predel
4. Promezhutochnyi sluchai
5. Spektral'naya diagnostika
6. Satellity

1. Vvedenie

Lineichatoe izluchenie - izluchenie nagretogo gaza (plazmy) na opredelennyh chastotah, nablyudaemoe v forme diskretnyh spektral'nyh linii. L. i. obrazuetsya vo vnesh. chastyah atmosfer zvezd (hromosfere, korone), mezhzvezdnoi i mezhgalaktich. srede, akkreciruyushem gaze rentgenovskih istochnikov i dr. Fotony L. i. ispuskayutsya otdel'nymi atomami (ionami, molekulami), okazavshimisya v vozbuzhdennom sostoyanii, pri perehodah v nih elektrona na bolee nizkii uroven' energii (v chastnosti, v osn. energetich. sostoyanie). Ispushennyi atomom foton mozhet libo vyiti iz ob'ema plazmy i dostich' nablyudatelya, libo poglotit'sya odnim iz okruzhayushih atomov. V poslednem sluchae atom, poglotivshii foton, okazyvaetsya v vozbuzhdennom sostoyanii i mozhet vnov' ispustit' foton s energiei $\varepsilon=h\nu$ , no, voobshe govorya, uzhe dr. chastoty (sm. Vzaimodeistvie izlucheniya s veshestvom). Esli izluchenie i pogloshenie proishodyat mnogokratno, spektr. liniya sil'no ushiryaetsya. Deistvitel'no, foton s chastotoi, blizkoi k chastote centra linii, s bol'shoi veroyatnost'yu pogloshaetsya vnov', a foton s chastotoi, dalekoi ot centra linii, legko vyhodit iz ob'ema. Poetomu veroyatnost' vyhoda fotona v "kryl'yah" linii effektivno vozrastaet, t.e. liniya ushiryaetsya. V predele liniya ischezaet - slivaetsya s nepreryvnym spektrom. Poetomu L. i. sohranyaetsya lish' v sluchae ne slishkom bol'shoi plotnosti i razmerov izluchayushei sredy.

L. i. neset vazhnuyu informaciyu o sostoyanii i fiz. processah v izluchayushei srede (sm. nizhe razdel Spektral'naya diagnostika). Naibolee prosta spektr. diagnostika plazmy v sluchae, kogda veroyatnost' vtorichnogo poglosheniya ispushennogo v lyuboi tochke fotona mala, t.e. izluchenie svobodno vyhodit iz ob'ema. Takoi sluchai naz. opticheski tonkoi plazmoi. Nizhe rassmatrivaetsya imenno etot sluchai. O formirovanii spektr. linii v usloviyah sushestvennogo poglosheniya fotonov (opticheski tolstaya plazma) sm. v st. Atmosfery zvezd.

Rassmotrim ispuskanie fotona k.-l. spektr. linii pri perehode elektrona v ione X_z s urovnya k (s energiei $\varepsilon_k$ ) na uroven' k' ( $\varepsilon_{k'}$ ). Zdes' H - k.-l. element, a z - spektroskopich. simvol iona, k-ryi na 1 bol'she kratnosti iona, t.e. H_z = H^(z-1)+ (sm. Ionizaciya).

Chastota ispushennogo fotona tex>(\varepsilon_k-\varepsilon_{k'})/h zavisit ot kvantovyh chisel k i k' urovnei energii i, krome togo, bystro rastet (~ z²) s rostom z. Sootvetstvenno foton mozhet okazat'sya v razlichnyh oblastyah spektra - ot radio- do rentgenovskoi. Tak, v hromosferah zvezd, gde T ~ 10⁴ K, obrazuyutsya gl. obr. linii neitral'nyh atomov i pervyh ionov (s z = 2) v UF- i vidimoi oblastyah. Osn. chast' L. i. solnechnoi korony, gde $T\approx 2\cdot 10^6$ K, prihoditsya na rezonansnye linii ionov s z = 8-12, lezhashie v rentg. oblasti (10-40 $\AA$ ) i dal'nei UF-oblasti (100-300 $\AA$ ). Nakonec, horosho izvestny rekombinacionnye radiolinii, svyazannye s perehodami mezhdu vysokovozbuzhdennymi urovnyami s glavnym kvantovym chislom n ~ 100 ili s perehodami mezhdu komponentami sverhtonkoi struktury urovnei energii (napr., radioliniya vodoroda 21 sm).

Svetimost' L_kk' izluchayushego ob'ema V plazmy v spektr. linii $k\to k'$ ravna:
$L_{kk'}=VN_k(X,z) A_{kk'}\varepsilon_{kk'}$ , (1)
gde A_kk' - veroyatnost' perehoda $k\to k'$ (t.e. chislo perehodov v ed. vremeni na odin atom), a N_k(X,z) - koncentraciya ionov H_z, nahodyashihsya na vozbuzhdennom urovne k. Udobno vyrazit' N_k(X,z) cherez otnositel'nuyu koncentraciyu n_z=N_k(X,z)/N(X) ionov H_z i naselennost' urovnya k: n_k=N_k(X,z)/N(X,z). Krome togo, v astrofizike prinyato vyrazhat' kolichestvo atomov v ed. ob'ema, t.e. koncentraciyu atomov N(X) cherez obilie $\alpha$ elementa H otnositel'no vodoroda: $\alpha$ (H)= N(X)/N_H. Poetomu f-lu (1) mozhno predstavit' v vide:
$L_{kk'}=VN_{\rm H}\alpha({\rm X}) n_z n_k A_{kk'}\varepsilon_{kk'}$ . (2)

Otnositel'naya koncentraciya ionov n_k opredelyaetsya ionizacionnym ravnovesiem v plazme, t.e. dinamich. ravnovesiem processov ionizacii i rekombinacii. Ochen' vazhno pri etom, chto pri stolknovenii elektrona s ionom veroyatnost' ionizacii namnogo bol'she, chem veroyatnost' rekombinacii. Poetomu maksimum funkcii n_k(T) dostigaetsya uzhe pri sravnitel'no nizkoi temp-re T, kogda $kT\ll\chi_z$ ( $\chi_z$ - energiya ionizacii iona H_z) i, sledovatel'no, eshe mala dolya elektronov, imeyushih dostatochnuyu energiyu, chtoby ionizovat' atom. Dlya bol'shinstva urovnei energiya vozbuzhdeniya urovnya iz osn. sostoyaniya E_k0 poryadka $\chi_z$ . T.o., v oblasti maksimuma otnositel'noi koncentracii n_k(T)
$\varepsilon_{k0},\chi_z\gg kT$ . (3)
Otmetim, chto s rostom z otnoshenie $\chi_z/kT$ stanovitsya men'she. Neobhodimye dlya podderzhaniya ionizac. ravnovesiya vozbuzhdenie i ionizaciya atomov osushestvlyayutsya elektronami s energiei $\varepsilon>kT$ , t.e. otnositel'no nebol'shim chislom elektronov s vysokoi energiei, obrazuyushih "hvost" Maksvella raspredeleniya.

2. Lokal'noe termodinamicheskoe ravnovesie

Naselennosti urovnei n_k i, sledovatel'no, harakteristiki spektra L. i. okazyvayutsya sushestvenno razlichnymi v sluchayah plotnoi i razrezhennoi plazmy. Fizicheski eto opredelyaetsya konkurenciei processov izluchatel'nogo perehoda (t.e. spontannogo ispuskaniya fotona) i bezyzluchatel'nogo perehoda pri stolknovenii vozbuzhdennogo atoma so svobodnym elektronom (t.n. tushashee stolknovenie s peredachei izbytka energii svobodnomu elektronu). Nizhe budut rassmotreny predel'nye sluchai: lokal'noe termodinamich. ravnovesie (bol'shaya plotnost' plazmy) i koronal'nyi predel (nizkaya plotnost').

Chastota tushashih stolknovenii proporcional'na koncentracii elektronov. Pri dostatochno bol'shoi koncentracii ona namnogo prevyshaet chislo izluchatel'nyh perehodov. Poetomu izluchenie prakticheski ne vliyaet na naselennosti vozbuzhdennyh urovnei, i, sledovatel'no, naselennosti opredelyayutsya zakonami termodinamiki, t.e. dayutsya Bol'cmana raspredeleniem:
$n_k=n_0\;\left({g_k\over {g_0}}\right)\;e^{-\beta_{k0}}$ , gde $\beta_{k0}={\varepsilon_k-\varepsilon_0\over{kT}}$ . (4)
V f-le (4) indeks 0 sootvetstvuet osn. sostoyaniyu, g_k i g₀ - statisticheskie vesa (oni opredelyayut chislo sostoyanii s dannoi energiei - stepen' vyrozhdeniya urovnya), $\varepsilon_k$ i $\varepsilon_0$ - energii urovnei. Sledovatel'no, n_k zavisit tol'ko ot T i $\varepsilon_k$ , a intensivnost' linii, soglasno (2), proporcional'na veroyatnosti perehoda A_kk'.

Soglasno neravenstvu (3), naselennosti vozbuzhdennyh sostoyanii, kak pravilo, maly i pochti vse atomy (iony) nahodyatsya v osn. sostoyanii, t.e. $n_0\approx 1$ .

Veroyatnosti perehodov A_kk' udovletvoryayut opredelennym pravilam otbora, nakladyvayushim ogranicheniya na vozmozhnye izmeneniya kvantovyh chisel pri perehodah. Sostoyanie atoma harakterizuetsya naborom kvantovyh chisel $k=\{\gamma, n, l, L, S, J\}$ , gde n i l - glavnoe i orbital'noe kvantovye chisla elektrona, sovershayushego perehod (t.n. optich. elektrona), $\gamma$ - sovokupnost' kvantovyh chisel, opisyvayushih prochie elektrony atoma, a L, S, J - orbital'nyi, spinovyi i polnyi momenty atoma v celom. Pri perehode $k\to k'$ izmenyaetsya chetnost' sostoyaniya (t.e. $\Delta l=\pm 1$ ), spin ne menyaetsya ( $\Delta S=0$ ), momenty L i J izmenyayutsya ne bolee chem na edinicu. Perehody, ne udovletvoryayushie etim pravilam otbora, naz. zapreshennymi.

V deistvitel'nosti po ryadu prichin veroyatnost' zapreshennyh perehodov $A_{kk'}\ne 0$ , no ona na nesk. poryadkov men'she, chem dlya razreshennyh perehodov. Poskol'ku intensivnost' L. i. proporcional'na A_kk', zapreshennye linii okazyvayutsya chrezvychaino slabymi. S rostom z stepen' zapreta ubyvaet.

Podobnye usloviya chasto naz. lokal'nym termodinamicheskim ravnovesiem (LTR), imeya v vidu termodinamicheskoe ravnovesie po otnosheniyu k naselennosti vozbuzhdennyh sostoyanii i ionizac. sostoyaniyu atomov i ionov. Esli, odnako, izluchayushii ob'em yavl. opticheski tonkim (kak predpolagalos' vyshe), to samo izluchenie daleko ot termodinamicheski ravnovesnogo, k-roe daetsya Planka zakonom izlucheniya.

LTR imeet mesto, napr., v hromosferah Solnca i zvezd, pravda, opticheskaya tolsha tam ne vsegda mala. V usloviyah LTR raspredelenie atomov po vozbuzhdennym urovnyam opredelyaetsya f-loi Bol'cmana (4), raspredelenie po sostoyaniyam ionizacii - Saha formuloi, a raspredelenie svobodnyh chastic po energii - f-loi Maksvella. Pri narushenii termodinamich. ravnovesiya (napr., pri nizkih plotnostyah, sm. nizhe) raspredeleniya Bol'cmana i Saha ne imeyut mesta. Odnako raspredelenie Maksvella imeet gorazdo bolee shirokuyu primenimost' i sohranyaetsya dazhe pri predel'no nizkih plotnostyah.

3. Koronal'nyi predel

Predel, protivopolozhnyi termodinamicheskomu, sootvetstvuet nizkoi plotnosti i chasto naz. koronal'nym predelom (KP), t.k. horosho realizuetsya v usloviyah solnechnoi korony, gde nizka elektronnaya koncentraciya (N_e ~ 10⁸-10⁹ sm^-3). Poskol'ku chastota tushashih stolknovenii proporcional'na N_e, stolknoveniyami mozhno prenebrech'. Poetomu naselennosti urovnei sootvetstvuyut ravnovesiyu mezhdu vozbuzhdeniem elektronnymi udarami i izluchatel'nymi spontannymi perehodami. T.k. eti dva processa raznoi prirody (v otlichie ot processov vozbuzhdeniya i tusheniya elektronami), usloviya daleki ot termodinamicheskih.

Pri nizkih plotnostyah, voobshe govorya, povyshaetsya rol' vozmozhnyh vnesh. istochnikov izlucheniya. Pri etom naselennosti urovnei i sv-va L. i. sushestvenno otlichayutsya ot uslovii KP. Primerom mogut sluzhit' zony NII, kvazary i dr., gde ionizac. ravnovesie opredelyaetsya izlucheniem central'nogo goryachego tela i, sledovatel'no, bol'shuyu rol' igraet rekombinac. zaselenie urovnei.

Pri maksvellovskom raspredelenii elektronov po skorostyam, prinyatom i dlya KP, chislo elektronov s energiei $\varepsilon>\varepsilon_{k0}$ , t.e. dostatochnoi dlya vozbuzhdeniya urovnya k, $\sim \exp(-\varepsilon_{k0}/kT)$ . Poetomu chastotu stolknovenii, privodyashih k vozbuzhdeniyu, mozhno zapisat' v vide: $N_e q_{k0} \exp(-\varepsilon_{k0}/kT)$ , gde koeff. q_k0 opredelyaetsya secheniem vozbuzhdeniya. Naselennost' urovnei n_k v dannom sluchae opredelyaetsya balansom vozbuzhdeniya udarami elektronov i izluchatel'nyh perehodov:
$n_k=N_e\;\left({q_{0k}\over {A_k}}\right)\;e^{-\beta_{k0}}$ , (5)
gde $A_k\sum\limits_{k'}A_{kk'}$ - polnaya veroyatnost' izluchatel'nogo raspada urovnya k (t.e. vseh vozmozhnyh izluchatel'nyh perehodov na nizhelezhashie urovni). Kak vidno, osn. zavisimost' n_k ot temp-ry v KP, kak i v LTR, daetsya eksponencial'nym faktorom $\exp(-\beta_{k0})$ . Odnako, v otlichie ot (4), naselennosti okazyvayutsya teper' proporcional'nymi N_e i zavisyat ot skorostei elementarnyh processov q_k0 i A_k. Poskol'ku N_e predpolagaetsya maloi, $N_e q_{0k}/A_k\ll 1$ , t.e. $n_k (k\ne 0)$ mnogo men'she, chem v usloviyah termodinamich. ravnovesiya, vozbuzhdenie udarami elektronov osushestvlyaetsya tol'ko iz osn. sostoyaniya.

F-la dlya svetimosti v linii L_kk' poluchaetsya pri podstanovke vyrazheniya (5) v f-lu (2):
$L_{kk'}=VN_{\rm H}N_e\alpha({\rm X}) n_z q_{0k} \left({A_{kk'}\over {A_k}} \right) \varepsilon_{kk'}\;e^{-\beta_{k0}}$ . (6)
Otnoshenie A_kk' /A_k naz. faktorom vetvleniya. Dlya pervyh vozbuzhdennyh sostoyanii vozmozhen lish' odin perehod s urovnya k i faktor vetvleniya raven 1. Pri etom L_kk' ne zavisit ot veroyatnosti perehoda, t.e. svetimosti dlya razreshennyh i zapreshennyh perehodov okazyvayutsya odnogo poryadka. Eto legko ponyat': vvidu otsutstviya tushashih stolknovenii atom, vozbuzhdennyi na uroven' k, ostaetsya na nem, poka ne proizoidet izluchatel'nyi perehod. Strogo govorya, ukazannoe sv-vo otnositsya lish' k metastabil'nym urovnyam, dlya k-ryh net konkuriruyushih razreshennyh perehodov na drugoi uroven', t.e. vetvlenie otsutstvuet (A_kk'=A_k). Nalichie v spektre yarkih zapreshennyh linii yavlyaetsya glavnym otlichiem KP ot LTR, gde L_kk'~ A_kk' , t.e. zapreshennye linii chrezvychaino slaby.

V kachestve primera mozhno privesti harakternuyu troiku linii geliepodobnyh ionov v rentg. spektrah solnechnoi korony: rezonansnuyu, interkombinacionnuyu (perehod s izmeneniem spina) i zapreshennuyu. Nablyudaemye intensivnosti etih linii otnosyatsya priblizitel'no kak 1:0, 3:0,8, hotya stepen' zapreta poslednei chrezvychaino velika - dostigaet 10⁹ pri z = 10 (s rostom z stepen' zapreta oslabevaet). Pomimo vozbuzhdeniya udarami elektronov zaselenie urovnya k vozmozhno takzhe za schet izluchatel'nyh kaskadnyh perehodov s bolee vysokih urovnei energii i pri rekombinacii na vozbuzhdennye urovni. Dlya "sil'nyh" linii (napr., rezonansnyh) rol' kaskadnyh processov i rekombinac. zaseleniya urovnei, kak pravilo, mala - ne prevoshodit 20%. Odnako dlya urovnei s maloi veroyatnost'yu pryamogo vozbuzhdeniya rol' etih processov mozhet byt' sushestvennoi. V chastnosti, dielektronnaya rekombinaciya mozhet igrat' opredelyayushuyu rol' dlya zaseleniya vysokih urovnei s glavnym kvantovym chislom $n\gg 1$ .

Drugim vazhnym sv-vom KP yavl. zavisimost' [sm. (6)]:
$L_{kk'}\sim N_{\rm H}N_eV\sim N_e^2 V$ . (7)
Velichina $N_e^2 V=$ ME naz. ob'emnoi meroi emissii. T.o., v KP svetimost' L_kk' ~ ME, v to vremya kak v usloviyah LTR, soglasno (4) i (2), L_kk' ~ N_HV, t.e. proporcional'na chislu izluchayushih atomov.

4. Promezhutochnyi sluchai

V obshem sluchae, kogda fiz. sostoyanie plazmy ne otvechaet ni usloviyam LTR, ni usloviyam KP, naselennosti opredelyayutsya balansom vseh processov zaseleniya i raspada urovnei, vklyuchaya tushashie stolknoveniya i stupenchatoe vozbuzhdenie, k-rye v KP ne igrali roli. Dlya nahozhdeniya n_k (a sledovatel'no, i intensivnostei spektr. linii) prihoditsya reshat' ves'ma gromozdkuyu sistemu algebraich. ur-nii balansa. Reshenie etih ur-nii pozvolyaet sdelat' sleduyushie vyvody. Pri nizkoi plotnosti plazmy (t.e. pri KP) i fiksirovannom chisle atomov N_HV svetimost' L_kk' ~ N_e. S rostom plotnosti "vklyuchayutsya" tushashie stolknoveniya, rost L_kk' zamedlyaetsya i v predele LTR L_kk' uzhe ne zavisit ot koncentracii elektronov N_e. Odnako rost L_kk' s uvelicheniem N_e mozhet prekratit'sya znachitel'no ran'she ustanovleniya LTR. Oboznachim $N_e^*$ elektronnuyu koncentraciyu, pri k-roi tushashie stolknoveniya nachinayut skazyvat'sya na naselennosti urovnya k i, sledovatel'no, narushat' usloviya KP. Priblizhenno
$N^*_e\approx {A_k\over {q_k}}, q_k= \sum\limits_{j\ne k} q_{jk}$ , (8)
gde q_k - summarnaya skorost' tushashih stolknovenii. Dlya zapreshennyh linii A_k malo i usloviya KP narushayutsya pri znachitel'no men'shei koncentracii N_e, chem dlya razreshennyh. Drugimi slovami, rost L_kk' s uvelicheniem koncentracii elektronov dlya zapreshennyh linii prekrashaetsya znachitel'no ran'she, t.e. na bolee nizkom urovne, chem dlya razreshennyh linii.

Skorost' tushashih stolknovenii q_kj rastet s umen'sheniem rasstoyaniya mezhdu urovnyami | $\varepsilon_k-\varepsilon_j$ |. Poetomu oni perevodyat atom s urovnya k ne v osn. sostoyanie, a na blizhaishii uroven', s k-rogo vozmozhen izluchatel'nyi perehod. Eto oznachaet, chto pri $N_e > N_e^*(k)$ svetimost' snachala "perekachivaetsya" iz zapreshennyh linii v razreshennye. Lish' zatem, s rostom N_e, nastupayut usloviya LTR dlya vseh linii.

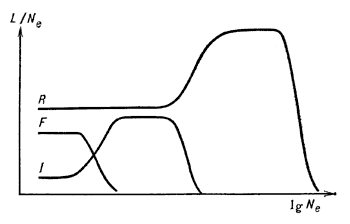
Ris. 1. Zavisimost' ot elektronnoi koncentracii
intensivnosti rezonansnoi (R),
interkombinacionnoi (I) i zapreshennoi (F) linii
geliepodobnogo iona. Masshtab po osi absciss
zavisit ot zaryada iona.

Na ris. 1 pokazano izmenenie s N_e svetimosti treh tipov linii geliepodobnogo iona: zapreshennoi (F), interkombinacionnoi (I) i rezonansnoi (R). Stepen' zapreta linii F na nesk. poryadkov sil'nee, chem linii I. Dlya udobstva po vertikal'noi osi otlozhena velichina L/N_e.

Znachenie q_kj, kak uzhe otmechalos', rastet s umen'sheniem rasstoyaniya mezhdu urovnyami. Veroyatnost' izluchatel'nyh perehodov mezhdu takimi urovnyami, naoborot, ubyvaet. Iz etogo vytekayut dva vazhnyh sledstviya.

1. Dlya vysokih urovnei energii atomov (kogda kvantovoe chislo n veliko) rasstoyanie mezhdu urovnyami umen'shaetsya, i, sledovatel'no, $N_e^*$ umen'shaetsya. Poetomu imeetsya tendenciya k termodinamicheski ravnovesnomu raspredeleniyu naselennostei mezhdu vysokimi urovnyami. Pri etom raspredelenie naselennostei prosto sleduet statistich. vesu (eksponenc. faktor dlya blizkih urovnei odinakov), a intensivnost' linii proporcional'na A_kk'.

2. Dlya ionov energii urovnei rastut ~ Z₂, a $N_e^*$ rastet kak Z₆ ili Z₇ dlya razreshennyh perehodov i eshe bystree dlya zapreshennyh. Poetomu dlya mnogozaryadnyh ionov (t.e. pri vysokih temp-rah) $N_e^*$ veliko, vliyanie tushashih stolknovenii neznachitel'no i KP imeet mesto prakticheski pri vseh plotnostyah, vstrechayushihsya v astrofizich. usloviyah.

5. Spektral'naya diagnostika

L. i. mozhet ispol'zovat'sya dlya opredeleniya temp-ry T i elektronnoi koncentracii N_e plazmy. Kak uzhe otmechalos', temperaturnaya zavisimost' intensivnosti linii v usloviyah LTR i KP analogichna ( $L_{kk'}\sim e^{-\beta_{k0}}$ ). Temp-ra mozhet byt' opredelena po spektr. liniyam kak ionov odnogo tipa, tak i ionov razlichnyh tipov. Ochen' udobny dlya opredeleniya T linii-satellity v spektrah mnogozaryadnyh ionov (sm. nizhe).

Sootnoshenie (8) yavl. osnovoi spektr. diagnostiki plotnosti plazmy (pri malyh i umerennyh plotnostyah). Pri etom naibolee udobno sravnivat' intensivnosti zapreshennoi i razreshennoi linii, polagaya, chto dlya poslednei KP vypolnyaetsya (odnovremenno mozhet vypolnyat'sya KP po odnim liniyam i LTR po drugim). Esli otnoshenie intensivnostei otlichaetsya ot vychislennogo s pomosh'yu f-l (5) ili (7), to $N_e\ge N_e^*(k)$ dlya sootvetstvuyushei zapreshennoi linii. Velichina $N_e^*$ opredelyaetsya po izvestnym znacheniyam A_k i q_k s pomosh'yu (slegka utochnennogo) sootnosheniya (8). Ispol'zuya razlichnye zapreshennye linii, mozhno ocenivat' N_e v razlichnyh diapazonah (sr. ris. 1).

V nek-ryh sluchayah okazyvaetsya udobnym ispol'zovat' dlya opredeleniya N_e abs. svetimosti
$L_{kk'}\sim N^2_e V$ (KP),
$L_{kk'}\sim N_{\rm H} V$ (LTR).(9)

V usloviyah, dalekih ot termodinamich. ravnovesiya, L. i. daet vozmozhnost' opredelit' T, N_e i obilie elementov $\alpha$ (H), a takzhe poluchit' detal'nuyu informaciyu o processah v plazme. S rostom plotnosti plazmy chislo odnovremenno proishodyashih mikroprocessov uvelichivaetsya i poluchit' detal'nuyu informaciyu ob otdel'nyh processah okazyvaetsya uzhe nevozmozhnym. V usloviyah LTR informaciya ob otdel'nyh mikroprocessah polnost'yu utrachivaetsya i okazyvaetsya vozmozhnym opredelyat' lish' makroharakteristiki: $T, N_e, \alpha$ (X); prichem dlya opredeleniya N_e neobhodimy abs. izmereniya libo linii raznyh ionov (pol'zuyutsya f-loi Saha). Nakonec, v opticheski tolstoi plazme pri polnom termodinamich. ravnovesii chastic i izlucheniya poslednee imeet plankovskuyu zavisimost' intensivnosti ot chastoty. Pri etom teryaetsya informaciya kak o N_e, tak i o $\alpha$ (H), t.e. po harakteru raspredeleniya energii v spektre mozhno opredelit' lish' temp-ru plazmy.

6. Satellity

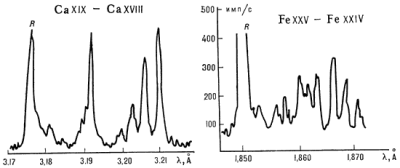
Ris. 2. Satellitnaya struktura okolo rezonansnoi linii (R)
geliepodobnogo iona: sleva - lazernaya plazma; sprava -
solnechnaya korona.

Osobuyu kategoriyu linii v spektre mnogozaryadnyh ionov H_z sostavlyayut satellity rezonansnoi i dr. linii. Satellity voznikayut pri perehodah mezhdu temi zhe urovnyami, chto i osn. liniya, no okazyvayutsya neskol'ko smeshennymi po chastote iz-za prisutstviya odnogo (ili neskol'kih) dopolnitel'nyh elektronov na vozbuzhdennom urovne nl. Nalichie dopolnitel'nogo nl-elektrona obuslovleno, kak pravilo, rekombinac. zahvatom (dielektronnaya rekombinaciya - osn. mehanizm obrazovaniya satellitov). Vozbuzhdennyi ion mozhet ispustit' libo elektron (i vernut'sya v ishodnoe sostoyanie), libo foton s chastotoi, blizkoi k chastote osn. linii (satellit). Pri n = 2 ili 3 satellity horosho razreshayutsya ot osn. linii, a pri $n\ge 4$ obychno slivayutsya s nei.

Otnoshenie intensivnostei satellita i osn. linii malo pri Z < 10 i bystro rastet (~ Z⁴) s rostom Z. Pri $Z\ge 20$ intensivnost' satellitov stanovitsya poryadka intensivnosti osn. linii i dalee pochti ne menyaetsya s uvelicheniem Z. Otnoshenie intensivnostei zavisit ot temp-ry. Deistvitel'no, vozbuzhdenie satellita soprovozhdaetsya zahvatom elektrona na uroven' s otricat. energiei $-\delta\varepsilon$ . Poetomu na vozbuzhdenie satellita trebuetsya men'she energii, chem na vozbuzhdenie osn. linii. Otnoshenie intensivnostei satellita i osn. linii $\sim\delta\beta\exp(\delta\beta)$ , gde $\delta\beta=\delta\varepsilon/kT$ . Iz f-ly vidno, chto s rostom temp-ry satellity stanovyatsya otnositel'no slabee. Poskol'ku satellity raspolozheny ves'ma blizko k osn. linii i vozbuzhdayutsya iz togo zhe osn. sostoyaniya, oni ves'ma udobny dlya opredeleniya temp-ry. Na ris. 2 pokazana satellitnaya struktura v oblasti rezonansnoi linii ionov CaXIX (lazernaya plazma) p FeXXV (solnechnaya korona, vspyshka). V poslednem sluchae struktura otnositel'no slabee vvidu bol'shei temperatury.

Lit.:
Vainshtein L.A., Sobel'man I.I., Yukov E.A., Vozbuzhdenie atomov i ushirenie spektral'nyh linii, M., 1979; Kaplan S.A., Pikel'ner S.B., Fizika mezhzvezdnoi sredy, M., 1979.

(L.A. Vainshtein)

L. A. Vainshtein, "Fizika Kosmosa", 1986
Glossarii Astronet.ru

L | R | A | B | V | G | D | E | Zh | Z | I | ' | K | L | M | N | O | P | R | S | T | U | F | H | C | Ch | Sh | Sh | E | Yu | Ya

Publikacii s klyuchevymi slovami: izluchenie v liniyah - spektral'nye linii - Spektr lineichatyi Publikacii so slovami: izluchenie v liniyah - spektral'nye linii - Spektr lineichatyi
Sm. takzhe: Vse cveta Solnca Solnechnyi spektr Zeemana effekt Laimana seriya Urovni energii (atomnye, molekulyarnye, yadernye) Laboratoriya issledovaniya zvezdnogo magnetizma SAO RAN Potoki iz chernoi dyry Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati