Astronet > Plazmennaya turbulentnost'

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Na saite

Astrometriya

Astronomicheskie instrumenty

Astronomicheskoe obrazovanie

Astrofizika

Istoriya astronomii

Kosmonavtika, issledovanie kosmosa

Lyubitel'skaya astronomiya

Planety i Solnechnaya sistema

Solnce

Plazmennaya turbulentnost'

1. Vvedenie
2. Kvazilineinaya teoriya
3. Inducirovannoe rasseyanie voln
4. Vzaimodeistvie volna-volna
5. Sil'naya lengmyurovskaya turbulentnost'

1. Vvedenie

P. t.- sostoyanie plazmy (P), v k-rom vozbuzhdeny intensivnye kolebaniya, imeyushie neregulyarnyi, shumovoi harakter. Po mere razvitiya fiziki kosmich. P. vse bolee yasnym stanovitsya tot fakt, chto uchet specifich. sv-v P. t., t. e. turbulentnosti razrezhennoi sredy s redkimi stolknoveniyami i dominiruyushim kollektivnym vzaimodeistviem, vazhen dlya pravil'nogo resheniya mnogih astrofizich. problem. V kachestve primera mozhno privesti fiziku magnitosfer planet i takie ee klyuchevye zadachi, kak zahvat i dinamika zaryazhennyh chastic v radiac. poyasah, mehanizmy anomal'no bystroi dissipacii energii solnechnogo vetra na fronte udarnoi volny magnitosfery, problemy peresoedineniya silovyh linii magn. polya i dr. Bez privlecheniya predstavlenii P. t., po-vidimomu, nevozmozhno ob'yasnit', naprimer, radioizluchenie Solnca, planet, vysokochastotnoe izluchenie pul'sarov.

Vo vseh perechislennyh sluchayah vozniknovenie turbulentnosti svyazano s neustoichivost'yu (N) ishodnogo sostoyaniya kosmich. P. Vsledstvie N amplitudy kolebanii P narastayut do nelineinogo urovnya, pri k-rom stanovyatsya sushestvennymi slozhnye processy vzaimodeistviya i vzaimnoi transformacii kolebanii. Zdes' imeetsya opredelennaya analogiya s gidrodinamich. turbulentnost'yu. Kak izvestno, pri bol'shih skorostyah potoka, t.e. pri bol'shih chislah Reinol'dsa, techenie stanovitsya neustoichivym i razbivaetsya na otdel'nye krupnomasshtabnye vihri. Vzaimodeistvie mezhdu vihryami privodit k nepreryvnomu drobleniyu ih masshtabov (t.e. vozniknoveniyu vse bolee melkih vihrei), proishodyashemu vplot' do podklyucheniya malyh masshtabov, dlya k-ryh sushestvenno zatuhanie, obuslovlennoe vyazkost'yu. Droblenie masshtabov vihrei sootvetstvuet perekachke energii turbulentnyh dvizhenii iz dlinnovolnovoi v korotkovolnovuyu oblast' spektra. Dr. primer takoi perekachki energii v gidrodinamich. turbulentnosti - eto ukruchenie (uvelichenie krutizny) i oprokidyvanie volnovogo fronta zvukovyh voln v zhidkosti i gaze.

Mezhdu plazmennoi i gidrodinamich. turbulentnostyami imeyutsya dva sushestvennyh razlichiya. Pervoe svyazano so specifich. sv-vami P, v k-roi dlya bol'shinstva vidov voln sushestvuet dispersiya fazovoi skorosti, t.e. zavisimost' fazovoi skorosti ot dliny volny (sm. Dispersiya voln). Rasplyvanie volnovyh paketov, obuslovlennoe dispersiei, sposobno ogranichivat' effekt ukrucheniya (podrobnee sm. v st. Besstolknovitel'nye udarnye volny). Vsledstvie etogo nepreryvno drobyashiesya vihri v P. t. ne obrazuyutsya, a proizvol'nye dvizheniya P vsegda mozhno predstavit' kak superpoziciyu vzaimodeistvuyushih mezhdu soboi ustanovivshihsya voln.

Vtoroe razlichie svyazano s tem, chto v P vazhnuyu, a inogda i opredelyayushuyu rol' igraet rezonansnoe vzaimodeistvie kolebanii i voln s chasticami, obuslovlennoe inducirovannymi (t.e. proishodyashimi "s pomosh'yu" uzhe imeyushihsya v dannoi spektr, oblasti kolebanii i voln) izlucheniem, poglosheniem i rasseyaniem voln chasticami (sm. nizhe). V ravnovesnoi P takoe vzaimodeistvie privodit k besstolknovitel'noi dissipacii voln (sm. Landau zatuhanie). V neravnovesnoi P mogut preobladat' processy inducirov. izlucheniya voln, privodyashie k razvitiyu mnogochisl. N. Obratnoe vozdeistvie voznikshih pri N kolebanii i voln na funkciyu raspredeleniya neustoichivogo sostoyaniya, stremyas' ustranit' ili, po krainei mere, ogranichit' faktor, vyzyvayushii N, privodit k besstolknovitelyyui relaksacii neustoichivogo raspredeleniya (anomal'no bystroe tormozhenie elektronnogo puchka v P, anomal'no bol'shoe soprotivlenie protekaniyu elektrich. toka, anomal'nye teploprovodnost', vyazkost' i dr.).

V P spektr vozmozhnyh kolebanii i voln (lengmyurovskie, ionno-zvukovye, al'venovskie i dr., sm. Plazma) nesravnenno bogache, chem v zhidkosti. Sootvetstvenno mozhno govorit' o razlichnyh tipah P. t. (lengmyurovskoi, ionno-zvukovoi i dr.). Vozmozhna takzhe smeshannaya turbulentnost', v k-roi prisutstvuet nesk. tipov vzaimodeistvuyushih voln. Po etoi prichine P. t. znachitel'no slozhnee gidrodinamich. turbulentnosti.

Obychnyi put' v izuchenii turbulentnyh processov v P sostoit prezhde vsego v issledovanii razlichnyh N (rassmotreny v st. Neustoichivosti plazmy), privodyashih k vozbuzhdeniyu intensivnyh kolebanii P, zatem issleduyutsya vozmozhnye mehanizmy nelineinogo ogranicheniya N i odnovremennogo razvitiya iz nih turbulentnyh processov v P.

Takoi put' chrezvychaino slozhen i do nastoyashego vremeni polnost'yu realizovan tol'ko dlya t.n. slaboi turbulentnosti P, teoriyu k-roi mozhno schitat' zavershennoi. Hotya ur-niya, opisyvayushie kolebaniya i volny v P, sushestvenno nelineiny, pri malyh amplitudah (malyh otkloneniyah ot ravnovesiya) v etih ur-niyah mozhno prenebrech' chlenami, soderzhashimi vtoroi i bolee vysokie poryadki amplitudy (chem vyshe poryadok, tem men'she velichina effekta, opisyvaemogo dannym chlenom). Dlya poluchayushihsya v takom priblizhenii voln i kolebanii P spravedliv princip superpozicii, t.e. otsutstvuet vzaimodeistvie mezhdu volnami. Sootvetstvuyushaya teoriya voln i kolebanii v P poluchila nazvanie lineinoi teorii. V teorii slaboi turbulentnosti amplitudy voln takzhe schitayutsya malymi - energiya volnovyh dvizhenii sushestvenno men'she teplovoi energii chastic. Poetomu zdes' ispol'zuyutsya te zhe volny i kolebaniya, chto i v lineinoi teorii, a proizvol'nye volnovye dvizheniya P predstavlyayutsya v vide razlozheniya po takim volnam. Odnako v ur-niyah dlya kolebanii i voln v P v etom sluchae sohranyayutsya malye nelineinye chleny, opisyvayushie vzaimodeistvie voln, a takzhe vzaimodeistvie mezhdu volnami i chasticami. Za schet takogo vzaimodeistviya amplitudy razlozhenii, t.e. amplitudy otdel'nyh voln, medlenno (po sravneniyu s periodom kolebanii) izmenyayutsya so vremenem.

2. Kvazilineinaya teoriya

V teorii slaboi turbulentnosti vzaimodeistvie voln i chastic obychno opisyvaetsya v ramkah kvazilineinogo priblizheniya. V takom priblizhenii kolebaniya i volny v P rassmatrivayutsya kak lineinye (prenebregaetsya vzaimodeistviem mezhdu volnami), a edinstvennym uchityvaemym nelineinym effektom yavl. izmenenie funkcii raspredeleniya rezonansnyh chastic (t.e. chastic, skorosti k-ryh udovletvoryayut usloviyu sootvetstvuyushego rezonansa) v rezul'tate inducirov. izlucheniya i poglosheniya voln etimi chasticami.

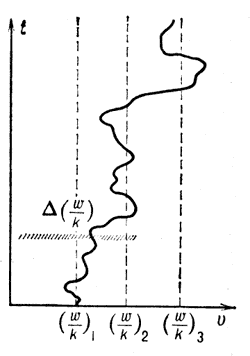
Ris. 1. Traektoriya chasticy v prostranstve
skorostei pri nalichii rezonansa s tremya
volnami. $\Delta(\omega/k)\approx\sqrt{e\varphi_0/m}$ - shirina otdel'nogo
rezonansa volna-chastica. Rezonansy dlya sosednih
voln perekryvayutsya. t - vremya, v - skorost'.

Prosteishii rezonans mezhdu volnami i chasticami - cherenkovskii, kogda proekcii skorosti chastic na napravlenie rasprostraneniya volny v_x, blizki k v_f - fazovoi skorosti volny: $v_x\approx v_{f}=\omega/k$ . V sluchae takogo rezonansa osn. nelineinyi mehanizm pri vzaimodeistvii chastic s otdel'noi (monohromaticheskoi) volnoi - zahvat rezonansnyh chastic v potencial'nuyu yamu, sozdannuyu volnoi, i ih kolebaniya v etoi yame. Sootvetstvenno shirina cherenkovskogo rezonansa poryadka skorosti kolebanii zahvachennyh chastic: $|v_x-\omega_k/k|\le\sqrt{q\varphi_0/m}$ , gde $\varphi_0$ - amplituda elektrich. potenciala v volne, q i m - zaryad i massa chasticy. Pri nalichii 2-3 voln tochnaya zadacha o dvizhenii rezonansnyh chastic stanovitsya chrezvychaino slozhnoi. V kvazilineinoi teorii, odnako, ispol'zuetsya priblizhennyi statistich. podhod, osnovannyi na predpolozhenii o tom, chto v neustoichivoi P vozbuzhdaetsya mnogo voln so sluchainymi fazami i blizkimi znacheniyami fazovoi skorosti, tak chto oblasti rezonansa dlya sosednih voln perekryvayutsya. Pri etom proishodit svoego roda "kollektivizaciya" rezonansnyh chastic mezhdu sosednimi volnami. V rezul'tate sluchainyh tolchkov so storony mnogih voln proishodit diffuziya chastic po skorosti (t.e. rasplyvanie oblasti, zanyatoi chasticami v prostranstve skorostei). Traektorii chastic v prostranstve skorostei predstavlyayut soboi brounovskoe bluzhdanie, nalozhennoe na svobodnoe dvizhenie chastic (ris. 1). S techeniem vremeni traektorii dostatochno plotno zapolnyayut ves' interval skorostei chastic, rezonansnyh s prisutstvuyushimi v P volnami $(\omega/k)_{min} < v < (\omega/k)_{maks}$ - v rezul'tate diffuzii funkciya raspredeleniya budet vyravnivat'sya, t.e. na nei poyavitsya "plato" vo vsem ukazannom intervale skorostei. Takoi process v fizike P obychno naz. kvazilineinoi relaksaciei neustoichivoi funkcii raspredeleniya.

V kachestve primera rassmotrim kvazilineinuyu relaksaciyu elektronnogo puchka v P. V etom sluchae verhnyaya granica "plato" blizka k nachal'noi skorosti puchka u₀, v to vremya kak nizhnyaya granica sravnima s teplovoi skorost'yu elektronov P v_Te (ris. 2). Dostatochno bystryi ( $u_0\gg v_{T_e}$ ) elektronnyi puchok v rezul'tate kvazilineinoi relaksacii teryaet (za vremya $\approx$ 5-10 obratnyh inkrementov puchkovoi N) na vozbuzhdenie kolebanii 2/3 svoei pervonachal'noi energii.

Neskol'ko slozhnee process kvazilineinoi relaksacii pri ciklotronnoi N. Eta N voznikaet v P, pomeshennoi v magn. pole, kogda f-ciya raspredeleniya po skorostyam anizotropna, t.e. sr. energiya vdol' magn. polya otlichna ot sr. energii poperek polya. N takogo raspredeleniya obuslovlena ciklotronnym inducirov. izlucheniem el.-magn. voln rezonansnymi chasticami. Vozbuzhdayutsya svistyashie atmosferiki (svisty), esli rezonansnye chasticy - elektrony, i al'venovskie volny v sluchae rezonansa s protonami. Uslovie ciklotronnogo rezonansa: $\omega-k_{||}/v_{||}=\omega_H$ . Poskol'ku chastota izluchaemoi volny $\omega$ men'she ciklotronnoi chastoty $\omega_H$ , to skorosti rezonansnyh chastic vdol' magn. polya v_|| otricatel'ny, t.e. rezonansnye chasticy dvizhutsya v storonu, obratnuyu napravleniyu rasprostraneniya volny (k_|| - komponent volnovogo vektora, parallel'nyi magn. polyu).

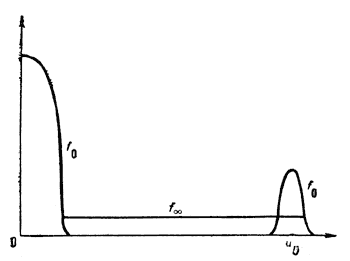
Ris. 2. Kvazilineinaya relaksaciya elektronnogo
puchka v plazme. f₀ - nachal'naya, neustoichivaya funkciya
raspredeleniya (maksimum pri v= 0 sootvetstvuet
ravnovesnoi plazme, maksimum pri v=u₀ - puchku),

Tak zhe kak i v sluchae cherenkovskogo rezonansa, ciklotronnoe izluchenie voln soprovozhdaetsya diffuziei rezonansnyh chastic v prostranstve skorostei. Odnako, v otlichie ot cherenkovskogo rezonansa, eta diffuziya yavl. dvuhmernoi - elektrich. pole el.-magn. volny E vyzyvaet poperechnuyu diffuziyu (t.e. izmenyaetsya perpendikulyarnyi magn. polyu komponent skorosti v_|| vpravo na velichinu fazovoi skorosti volny ubd/2005/01/15/0001201969/tex/formula10.gif" border="0" alt="$f_\infty$" align="absmiddle" width="19" height="16" > -
border="0" alt="$v_\perp$" align="absmiddle" width="17" height="11" >), a za schet sily Lorenca $e[{\bf v}_\perp{\bf H}]/c$ , svyazannoi s magn. polem volny, proishodit diffuziya chastic po prodol'noi border="0" alt="$v_\perp^2+(v_{||}-\omega/k)^2$" align="absmiddle" width="120" height="20" >=const 8%66%00%67%00%6A" >Magnitosfery planet). Dlya magnitosfery border="0" alt="$\sim\omega/\omega_H$" align="absmiddle" width="57" height="18" >) energii rezonansnyh chastic.

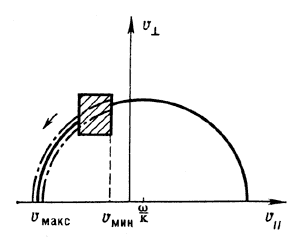
Ris. 3. Diffuziya chastic v prostranstve
skorostei v sluchae ciklotronnogo rezonansa
s volnami. Zashtrihovana oblast', v
kotoroi pervonachal'no nahodyatsya rezonansnye
chasticy, strelka pokazyvaet napravlenie
diffuzii. Diffuziya soprovozhdaetsya
izotropizaciei raspredeleniya rezonansnyh
chastic po skorostyam (shtrihpunktir) i
poterei imi chasti energii, perehodyashei
v kolebaniya. $v_{||}, v_\perp$ - parallel'naya
i perpendikulyarnaya magnitnomu polyu
sostavlyayushie skorosti.

Eshe odna vazhnaya dlya kosmich. fiziki N - t.n. shlangovaya. Ona takzhe razvivaetsya v anizotropnoi P. Dlya ee poyavleniya prodol'naya temp-ra i davlenie P dolzhny sushestvenno prevyshat' poperechnye. Za schet shlangovoi N magn. silovye linii izvivayutsya besporyadochnym obrazom, tak chto magn. pole turbulizuetsya. Obratnoe vliyanie etoi turbulentnosti na neustoichivuyu P mozhno ponyat', esli vospol'zovat'sya usloviyami sohraneniya adiabatich. invariantov: $mv_\perp^2/H={\rm const},\; \int v_{||}\;dl={\rm const}$ (integral vychislyaetsya vdol' silovoi linii magn. polya mezhdu tochkami otrazheniya chastic, dl - dlina elementa silovoi linii). Yasno, chto po mere rosta turbulentnogo magn. polya rastut poperechnye skorosti chastic $v_\perp$ (a sledovatel'no, i poperechnye davleniya) i umen'shayutsya prodol'nye skorosti i davlenie (poskol'ku pri zaputyvanii silovyh linii uvelichivaetsya dlina l). Davlenie izotropizuetsya, t.e. i v etom sluchae pod deistviem P. t. proishodit besstolknovitel'naya relaksaciya anizotropnoi P.

3. Inducirovannoe rasseyanie voln

Kvazilineinaya teoriya opisyvaet tol'ko processy inducirov. izlucheniya i poglosheniya voln rezonansnymi chasticami. Iz bol'shogo chisla, voobshe govorya, bolee slabyh nelineinyh effektov, voznikayushih v vysshih poryadkah po amplitude kolebanii, v teorii P. t. osobo vazhnaya rol' prinadlezhit effektu rezonansnogo vzaimodeistviya chastic s bieniyami raznostnoi chastoty mezhdu dvumya lyubymi kolebaniyami, vozbuzhdennymi v turbulentnoi P. Poskol'ku eti bieniya mozhno rassmatrivat', v opredelennom smysle, kak novye volny, to uslovie cherenkovskogo rezonansa chastic s nimi zapisyvaetsya v vide: $({\bf k-k_1)v}=\omega_k-\omega_{k_1}$ . Esli volny v turbulentnoi P rassmatrivat' kak gaz kvazichastic (elementarnyh volnovyh vozbuzhdenii - volnovyh kvantov) s energiei $\hbar \omega_k$ i impul'som $\hbar {\bf k}$ , to uslovie rezonansnogo vzaimodeistviya s bieniyami okazyvaetsya prostym sledstviem zakonov sohraneniya energii i impul'sa pri rasseyanii chasticei volnovogo kvanta (k, $\omega_k$ ) v volnovoi kvant (k₁, $\omega_{k_1}$ ). Poetomu rassmatrivaemyi nelineinyi process chasto naz. inducirov. rasseyaniem voln. Ego vazhnaya rol' svyazana s tem, chto dlya voln s maloi dispersiei chastoty (napr., dlya lengmyurovskih) fazovaya skorost' bienii $(\omega_k-\omega_{k_1})(k-k_1)$ nastol'ko mala, chto mozhet okazat'sya men'she teplovoi skorosti chastic. V etom sluchae v rezonans s bieniyami vovlekaetsya osn. massa teplovyh chastic P, v to vremya kak uslovie cherenkovskogo rezonansa pri inducirov. izluchenii i pogloshenii voln vypolnyaetsya tol'ko dlya nebol'shoi gruppy nadteplovyh chastic (puchka). Poetomu hotya rezonans na bieniyah nelineinyi, t.e. voznikaet v vysshih poryadkah po amplitude voln, iz-za bol'shego chisla rasseivayushih chastic on mozhet okazat'sya ves'ma sushestvennym v dinamike spektra voln. Pri rasseyanii na teplovyh chasticah P chastota rasseyannogo kvanta vsegda men'she chastoty ishodnogo, poskol'ku chast' energii peredaetsya rasseivayushei chastice (nelineinoe zatuhanie Landau). Dlya lengmyurovskih voln, kak, vprochem, i dlya dr. voln s norm. dispersiei ( $\omega$ rastet s k), takoe umen'shenie chastoty pri rasseyanii oznachaet umen'shenie volnovogo chisla. T.o., pri inducirov. rasseyanii lengmyurovskih voln spektr, perekachka energii proishodit v storonu bol'shih dlin voln, t.e. bol'shih fazovyh skorostei (v otlichie ot privychnoi kartiny - gidrodinamich. turbulentnosti, kogda perekachka energii proishodit ot bol'shih masshtabov k men'shim).

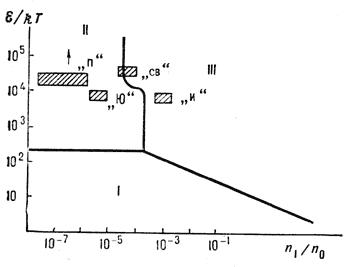
Ris. 4. Granicy deistviya razlichnyh mehanizmov
relaksacii elektronnyh puchkov v plazme: I -
kvazilineinaya teoriya, II - oblast'
inducirovannogo rasseyaniya, III - oblast', gde
sushestvenny effekty sil'noi turbulentnosti.
Otmecheny takzhe parametry razlichnyh
kosmicheskih yavlenii, dlya kotoryh sushestvenny
kollektivnye mehanizmy relaksacii puchkov v
plazme: "i" - potoki bystryh chastic,
pronikayushih v avroral'nyh oblastyah v
ionosferu, "sv" - elektronnye puchki,
voznikayushie pri hromosfernyh vspyshkah v
plazme solnechnogo vetra, "p" - elektronnye
puchki v magnitosferah pul'sarov, "Yu" - puchki,
vzaimodeistvuyushie s plazmoi solnechnogo vetra
v raione magnitopauzy Yupitera.

Odno iz vazhnyh sledstvii effekta inducirov. rasseyaniya voln - nelineinaya stabilizaciya puchkovoi N. V osnove puchkovoi N lezhit effekt inducirov. izlucheniya voln puchkom, kogda vozbuzhdeniyu voln s opredelennoi chastotoi i dlinoi volny "pomogayut" uzhe imeyushiesya v etoi spektral'noi oblasti volny. Esli skorost' spektr. perekachki, obuslovlennoi inducirov. rasseyaniem, dostatochno velika, to volny, uvelichivaya svoyu fazovuyu skorost', pokidayut rezonansnuyu s puchkom oblast' spektra, prezhde chem uspevayut effektivno s nim provzaimodeistvovat'. V rezul'tate dolzhna proishodit' stabilizaciya puchkovoi N. Real'no, odnako, energiya rezonansnyh s puchkom kolebanii vozrastaet do urovnya, pri k-rom skorosti oboih processov (skorost' rosta kolebanii iz-za N i skorost' spektr. perekachki) sravnivayutsya. Poskol'ku energiya rezonansnyh kolebanii pri etom mozhet okazat'sya sushestvenno men'she energii puchka, chasticy puchka budut kraine medlenno rasseivat'sya takimi kolebaniyami, i P stanovitsya kak by prozrachnoi dlya elektronnogo puchka. Na ris. 4 privedeny dlya ploskosti parametrov n₁/n₀, $\varepsilon/kT$ (n₁, n₀ - sootvetstvenno plotnosti puchka i P, $\varepsilon$ - energiya chastic puchka, T - temp-ra P) oblasti deistviya razlichnyh mehanizmov relaksacii puchka v P. Granica mezhdu oblast'yu primenimosti kvazilineinoi teorii i oblast'yu, gde sushestvenna nelineinaya stabilizaciya puchkovoi N iz-za inducirov. rasseyaniya, opredelyaetsya sootnosheniem: $\varepsilon/kT\approx[30 u_0 M/\Delta um_e]^{1/3}$ , gde M - massa iona, $\Delta u$ - razbros po skorostyam v puchke. Iz ris. 4 vidno, chto vo mnogih sluchayah (relyativistskie elektronnye puchki v magnitosferah pul'sarov, elektronnye puchki, vzaimodeistvuyushie s P solnechnogo vetra v raione udarnoi volny yupiterianskoi magnitosfery) dominiruet inducirov. rasseyanie, t.e. sushestven effekt "nelineinogo prosvetleniya" P dlya elektronov puchka.

4. Vzaimodeistvie volna-volna

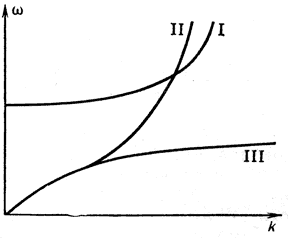
Ris. 5. Raspadnye (II) i neraspadnye (I, III)
spektry voln v plazme.

Do sih por my rassmatrivali effekty v turbulentnoi P, osnovannye na vzaimodeistvii volna-chastica. Odnako esli amplitudy voln ne slishkom maly, v dinamike turbulentnosti mogut stat' sushestvennymi effekty nelineinogo vzaimodeistviya mezhdu volnami. Esli ispol'zovat' analogiyu turbulentnoi P so smes'yu dvuh gazov - gaza chastic (elektronov, ionov) i gaza kvazichastic (elementarnyh volnovyh vozbuzhdenii), to eti novye nelineinye effekty mozhno interpretirovat' kak vzaimodeistviya vnutri gaza kvazichastic. Prosteishie vzaimodeistviya takogo tipa - raspady i sliyaniya v sisteme treh voln. Pri etom dolzhny vypolnyat'sya raspadnye usloviya dlya chastot i volnovyh vektorov vzaimodeistvuyushih voln: $\omega_k=\omega_{k_1}+\omega_{k_2}$ , k = k₁+k₂, yavlyayushiesya sledstviem zakonov sohraneniya energii i impul'sa volnovyh kvantov [privedennye raspadnye usloviya zapisany dlya raspada kvanta (k, $\omega_k$ ) na kvanty (k₁, $\omega_{k_1}$ ), (k₂, $\omega_{k_2}$ )]. Daleko ne vsyakii spektr plazmennyh kolebanii yavl. raspadnym, t.e. ne pri kazhdoi dispersionnoi zavisimosti ( $\omega({\bf k})$ ) mogut byt' vypolneny raspadnye usloviya. Na ris. 5 privedeny primery raspadnyh (II) i neraspadnyh (I, III) spektrov. Poskol'ku plazmennye kolebaniya imeyut mnozhestvo razlichnyh vetvei (vetvei dispersionnoi krivoi), to raspadnye usloviya mogut vypolnyat'sya dlya kolebanii, prinadlezhashih razlichnym vetvyam, esli tol'ko cherez tri tochki na etih vetvyah mozhno provesti krivuyu, analogichnuyu II. Napr., dlya lengmyurovskoi volny (spektr neraspadnyi) raspadnye usloviya vypolnyayutsya pri raspade na lengmyurovskuyu i ionno-zvukovuyu volny. Vozmozhny i dr. varianty konversii (vzaimnogo prevrasheniya) razlichnyh tipov voln v P, napr. rozhdenie lengmyurovskih i ionno-zvukovyh voln pri raspade el.-magn. volny. V teh sluchayah, kogda raspadnye usloviya dlya treh voln ne vypolnyayutsya, v elementarnyi akt vzaimodeistviya vklyuchayutsya srazu chetyre volny i sootvetstvenno etomu vzaimodeistvie mezhdu volnami v slaboi turbulentnosti stanovitsya bolee medlennym (pri trehvolnovyh vzaimodeistviyah obratnoe vremya evolyucii spektr. plotnosti chisla volnovyh kvantov N_k proporcional'no pervoi stepeni etoi plotnosti, v to vremya kak pri chetyrehvolnovyh vzaimodeistviyah eto vremya proporcional'no kvadratu plotnosti).

Evolyuciya spektrov voln, obuslovlennaya nelineinym vzaimodeistviem, opisyvaetsya kinetich. ur-niem dlya velichin N_k. Eto ur-nie krome ochevidnogo ravnovesnogo resheniya: raspredeleniya Releya-Dzhinsa $N_k={\rm const}/\omega_k$ - imeet takzhe stacionarnye resheniya s perenosom energii po spektru, t.e. v prostranstve volnovyh chisel. Eti resheniya sootvetstvuyut takoi situacii, kogda pritok energii v turbulentnye dvizheniya proishodit v oblasti bol'shih masshtabov, nelineinoe vzaimodeistvie sozdaet potok energii k men'shim masshtabam, dlya k-ryh sushestvenna dissipaciya. Zdes' imeetsya polnaya analogiya s gidrodinamich. turbulentnost'yu. Mezhdu krupnymi masshtabami oblasti pritoka energii i melkimi masshtabami oblasti zatuhaniya kolebanii nahoditsya t.n. inercionnyi interval, v k-rom spektr dlya mnogih tipov turbulentnosti imeet universal'nuyu formu, sootvetstvuyushuyu postoyanstvu potoka energii po spektru. V kachestve primera takoi turbulentnosti mozhno privesti ionno-zvukovuyu turbulentnost'. Process korotkovolnovoi perekachki energii v etom sluchae svyazan so sliyaniem ionno-zvukovyh kvantov s pochti kollinearnymi volnovymi vektorami. Kollinearnost' neobhodima dlya vypolneniya raspadnyh uslovii, poskol'ku spektr dlinnovolnovyh ionno-zvukovyh kolebanii blizok k lineinomu. Iz usloviya postoyanstva potoka energii po spektru sleduet, chto dlya kazhdogo masshtaba turbulentnosti r, imeyushego harakternye skorosti kolebanii chastic v, vypolneno sootnoshenie v⁴r= const, chto sootvetstvuet spektr. plotnosti ionno-zvukovyh kvantov: N_k= const /k^3/2.

5. Sil'naya lengmyurovskaya turbulentnost'

Znachitel'no slozhnee reshaetsya zadacha o turbulentnosti lengmyurovskih kolebanii i voln. Delo v tom, chto spektr lengmyurovskih voln - neraspadnyi i osnovnye nelineinye vzaimodeistviya dlya lengmyurovskih voln v slaboi turbulentnosti svyazany s uzhe opisannym vyshe processom inducirov. rasseyaniya voln na chasticah P libo s raspadom lengmyurovskoi volny na lengmyurovskuyu i ionno-zvukovuyu. Pri kazhdom iz etih processov dolzhno proishodit' "pokrasnenie" (uvelichenie dliny volny) lengmyurovskogo kvanta (plazmona), poskol'ku chast' energii plazmona peredaetsya libo rasseivayushei chastice, libo ionno-zvukovomu kvantu. T.o., nelineinoe vzaimodeistvie v lengmyurovskoi turbulentnosti sozdaet potok energii v dlinnovolnovuyu oblast', gde voobshe otsutstvuyut mehanizmy poglosheniya lengmyurovskih kolebanii. V rezul'tate voznikaet paradoks obrazovaniya plazmennogo kondensata: esli v P imeetsya istochnik lengmyurovskih kolebanii (puchok, el.-magn. volna), to v konechnom schete energiya etogo istochnika budet nakaplivat'sya v vide ochen' dlinnovolnovyh ( $k\to 0$ ) lengmyurovskih voln, ne pogloshayushihsya v P i budet neogranichenno narastat' so vremenem, chto v principe nevozmozhno. Reshenie etogo paradoksa nevozmozhno v ramkah slaboi turbulentnosti, ono osnovano (sm. nizhe) na ispol'zovanii modulyac. N lengmyurovskih voln. Eto N plazmennogo kondensata, t.e. dostatochno intensivnogo gaza dlinnovolnovyh plazmonov, otnositel'no processa modulyacii ego plotnosti. N privodit k obrazovaniyu kavern - oblastei povyshennoi koncentracii plazmonov, iz k-ryh pod deistviem sily vysokochastotnogo davleniya, sozdavaemogo plazmonami (analog davleniya izlucheniya), vytesnena P. Harakternyi razmer kavern, obrazuyushihsya v rezul'tate modulyac. N, $L\sim k^{-1}\sim D\sqrt{n_0/|\delta n|}$ obychno poryadka 10-30 debaevskih radiusov D ( $\delta n$ - variacii plotnosti P v kavernah). V laboratornoi P iz-za maloi velichiny D nablyudenie takih struktur kraine zatrudneno. Osn. nablyudeniya modulyac. N lengmyurovskih voln otnosyatsya k kosmich. usloviyam (razrezhennaya P, bol'shie D). Na ris. 6 pokazana prostranstv. struktura intensivnyh lengmyurovskih voln, vozbuzhdaemyh v P solnechnogo vetra v raione udarnoi volny yupiterianskoi magnitosfery, gde $D\approx$ 20 m, chto pozvolyaet otnositel'no legko razreshit' ("uvidet'") mikrostrukturu otdel'nyh kavern. V processe razvitiya modulyac. N plazmony okazyvayutsya zapertymi v kavernah, podobno tomu kak zaryazhennye chasticy zapirayutsya v dostatochno glubokih elektrich. potencial'nyh yamah. Etot nelineinyi effekt uzhe ne mozhet byt' opisan v ramkah slaboi turbulentnosti, t.e. v ramkah slabogo vzaimodeistviya kolebanii i voln lineinoi teorii. Poetomu prinyato schitat', chto modulyac. N privodit k sil'noi lengmyurovskoi turbulentnosti.

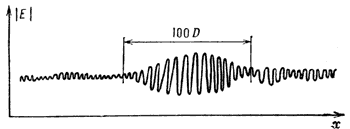
Ris. 6. Lengmyurovskaya kaverna v kosmicheskoi plazme
po dannym nablyudenii v raione magnitopauzy Yupitera.
|E| - modul' napryazhennosti elektricheskogo polya.

V teorii sil'noi lengmyurovskoi turbulentnosti vazhnoe znachenie imeet yavlenie kollapsa lengmyurovskih voln, t.e. samoproizvol'nogo shlopyvaniya kavern s zapertymi v nih plazmonami. Eto shlopyvanie nosit harakter "vzryva", t.e. proishodit s narastayushei skorost'yu vplot' do togo momenta, kogda kaverna dostigaet stol' malyh razmerov, chto dlina volny zapertyh v nei plazmonov sravnivaetsya s D, a fazovaya skorost' sootvetstvenno - s teplovoi skorost'yu. Pri etom vklyuchaetsya zatuhanie Landau lengmyurovskih kolebanii, i dissipaciya ih energii ostanavlivaet kollaps.

Teoriya sil'noi lengmyurovskoi turbulentnosti, baziruyushayasya na yavlenii kollapsa, okazyvaetsya v znachit. stepeni analogichnoi teorii gidrodinamich. turbulentnosti. Istochnik turbulentnosti nahoditsya v oblasti bol'shih masshtabov. Korotkovolnovaya perekachka lengmyurovskih kolebanii osushestvlyaetsya za schet shlopyvaniya kavern s zapertymi v nih plazmonami, v oblasti malyh masshtabov proishodit besstolknovitel'noe pogloshenie plazmonov. S etim i svyazano reshenie voznikayushego v teorii slaboi turbulentnosti paradoksa plazmennogo kondensata. Spektr. plotnost' plazmonov v inercionnom intervale mozhno naiti, ispol'zuya zakony shlopyvaniya kavern: N_k= const /k^5/2

V tom sluchae, kogda lengmyurovskie kolebaniya vozbuzhdayutsya pri vzaimodeistvii s P elektronnogo puchka, korotkovolnovaya spektr. perekachka kolebanii, obuslovlennaya modulyac. N i kollapsom, mozhet privodit' k stabilizacii puchkovoi N. Etot mehanizm stabilizacii puchkovoi N sushestven dlya puchkov vysokih energii i otnositel'no bol'shoi plotnosti (ris. 4): potoki bystryh elektronov, obrazuyushiesya v P solnechnogo vetra pri vspyshkah na Solnce, elektrony s vysokoi energiei, vtorgayushiesya v ionosferu v avroral'nyh oblastyah, i dr. Granica mezhdu oblast'yu III, gde sushestvenny effekty sil'noi turbulentnosti, i oblast'yu I, gde primenima kvazilineinaya teoriya relaksacii, opredelyaetsya sootnosheniem $n_1/n_0=10(kT/\varepsilon)^3 u_0/\Delta u$ . Granica mezhdu oblast'yu III i oblast'yu II, v k-roi sushestvenno inducirov. rasseyanie lengmyurovskih kolebanii chasticami P, opredelyaetsya sootnosheniem $n_1/n_0\approx m/3M$ v tom sluchae, kogda relaksiruyut puchki ne slishkom bol'shoi energii $(\varepsilon/kT\ll 3M/m)$ , i $n_1/n_0\approx(\Delta u/u)^2 m/3M$ v obratnom sluchae $(\varepsilon/kT\gg 3M/m)$ .

Skorost' spektr. perekachki lengmyurovskih kolebanii i ih posleduyushei dissipacii v sil'noi turbulentnosti obychno stol' velika, chto plotnost' energii vozbuzhdaemyh puchkom kolebanii W "zamorozhena" pa poroge modulyac. N: $W\approx 3k_0^2 D^2 n_0 kT, k_0\simeq\omega_{0e}/u_0$ - volnovoe chislo rezonansnyh s puchkom kolebanii. Prevyshenie etogo poroga privodit k tomu, chto process vozbuzhdeniya kolebanii uzhe ne mozhet konkurirovat' s ih dissipaciei i kolebaniya vnov' vozvrashayutsya na porog. Otnositel'no nizkii uroven' rezonansnyh s puchkom lengmyurovskih kolebanii privodit k sushestvennomu zatyagivaniyu processa kollektivnoi relaksacii puchka v P. Etot effekt imeet mesto, napr., dlya obrazuyushihsya pri vspyshkah na Solnce elektronnyh puchkov, vzaimodeistvuyushih s P solnechnogo vetra (ris. 7). Transformaciya lengmyurovskih kolebanii, vozbuzhdaemyh takimi puchkami, v el.-magp. izluchenie privodit k solnechnym radiovspleskam III tipa (sm. Radioizluchenie Solnca).

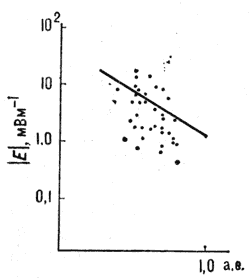
Ris. 7. Prostranstvennoe raspredelenie
energii plazmennyh kolebanii po dannym
nablyudenii v plazme solnechnogo vetra.
Sploshnaya liniya - teoreticheskaya ocenka po
porogu modulyacionnoi neustoichivosti. |E| -
modul' napryazhennosti elektricheskogo polya, po
gorizontal'noi osi - rasstoyanie ot Solnca.

Voobshe, dlya mnogih zadach astrofiziki (napr., radioizluchenie Solnca, planet) ves'ma vazhny mehanizmy transformacii lengmyurovskih kolebanii v el.-magn. volny. Naryadu so vspleskami III tipa effekty transformacii naibolee sushestvenny v solnechnyh radiovspleskah II tipa (prevrashenie v el.-magn. volny plazmennyh voln, generiruemyh na fronte udarnoi volny, obrazovannoi vspyshkoi na Solnce), v kilometrovom izluchenii Zemli (radioizluchenie lengmyurovskoi turbulentnosti, sozdavaemoi bystrymi potokami elektronov v magnitosfere) i vo mnogih dr. podobnyh effektah.

Vyshe bylo pokazano, chto raspad lengmyurovskih kolebanii mozhet idti tol'ko s umen'sheniem chastoty, t.e. ne mozhet neposredstvenno privodit' k transformacii v el.-magn. volny. Vmeste s tem neizbezhnym sputnikom sil'noi lengmyurovskoi turbulentnosti yavl. intensivnye kvazineitral'nye fluktuacii plotnosti P. Konversiya lengmyurovskih kolebanii na etih fluktuaciyah plotnosti dolzhna privodit' k ih transformacii v el.-magn. volny. Etot mehanizm, po-vidimomu, yavl. osnovnym v radiovspleskah III tipa. Vmeste s tem sushestvennym mozhet okazat'sya i dr. mehanizm transformacii v el.-magn. volny - sliyanie dvuh lengmyurovskih kvantov s obrazovaniem el.-magn. kvanta na udvoennoi lengmyurovskoi chastote. Poetomu pri solnechnyh vspleskah II i III tipov izluchenie poyavlyaetsya srazu na dvuh garmonikah, chastoty k-ryh otnosyatsya kak 2:1.

Lit.:
Arcimovich L.L., Sagdeev R.3., Fizika plazmy dlya fizikov, M., 1979; Kadomcev B. V., Kollektivyaye yavleniya v plazme, M., 1976; Vedenov A.A., Ryutov D. D., Kvazilineinye effekty v potokovyh neustoichivostyah, v sb.: Voprosy teorii plazmy, v. 6, M., 1972; Galeev A.A., Sagdeev R.3., Nelineinaya teoriya plazmy, tam zhe, v. 7, M., 1973; Pikel'ner S.B., Osnovy kosmicheskoi elektrodinamiki, 2 izd., M., 1966; Cytovich V.N., Nelineinye effekty v plazme, M., 1967; Gurnett D.A., Anderson R. V., "Science", v. 194, r. 1159.

(V.D. Shapiro)

V. D. Shapiro, "Fizika Kosmosa", 1986
Glossarii Astronet.ru

A | B | V | G | D | Z | I | K | L | M | N | O | P | R | S | T | U | F | H | C | Ch | Sh | E | Ya

Publikacii s klyuchevymi slovami: plazmennaya turbulentnost' - Plazma - turbulentnost' Publikacii so slovami: plazmennaya turbulentnost' - Plazma - turbulentnost'
Sm. takzhe: Odin god na Solnce "Z-mashina" ustanavlivaet neozhidannyi rekord temperatury na Zemle Al'venovskie volny v kollapsiruyushih protozvezdnyh oblakah Ot plazmy solnechnoi korony k plazme na neitronnyh zvezdah Plazma Tanec Solnca Turbulentnaya oblast' vokrug zvezdy Eta Kilya Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati