Rambler's Top100Astronet    
  po tekstam   po klyuchevym slovam   v glossarii   po saitam   perevod   po katalogu 		 

Urovni energii (atomnye, molekulyarnye, yadernye)

1. Harakteristiki sostoyaniya kvantovoi sistemy
2. Energeticheskie urov atomov
3. Energeticheskie urovni molekul
4. Energeticheskie urovni yader

1. Harakteristiki sostoyaniya kvantovoi sistemy

V osnove ob'yasneniya sv-v atomov, molekul i atomnyh yader, t.e. yavlenii, proishodyashih v elementah ob'ema s lineinymi masshtabami 10-6-10-13 sm, lezhit kvantovaya mehanika. Soglasno kvantovoi mehanike, vsyakaya kvantovaya sistema (t.e. sistema mikrochastic, k-raya podchinyaetsya kvantovym zakonam) harakterizuetsya opredelennym naborom sostoyanii. V obshem sluchae etot nabor sostoyanii mozhet byt' kak diskretnym (diskretnyi spektr sostoyanii), tak i nepreryvnym (nepreryvnyi spektr sostoyanii). Harakteristikami sostoyaniya izolirovannoi sistemy yavl. vnutrennyaya energiya sistemy (vsyudu dal'she prosto energiya), polnyi moment kolichestva dvizheniya (MKD) i chetnost'.

Energiya sistemy.
Kvantovaya sistema, nahodyas' v razlichnyh sostoyaniyah, obladaet, voobshe govorya, razlichnoi energiei. Energiya svyazannoi sistemy mozhet prinimat' lyubye znacheniya. Etot nabor vozmozhnyh znachenii energii naz. diskretnym energeticheskim spketrom, a ob energii govoryat, chto ona kvantuetsya. Primerom mozhet sluzhit' energetich. spektr atoma (sm. nizhe). Nesvyazannaya sistema vzaimodeistvuyushih chastic obladaet nepreryvnym energeticheskim spektrom, a energiya mozhet prinimat' proizvol'nye znacheniya. Primerom takoi sistemy yavl. svobodnyi elektron (E) v kulonovskom pole atomnogo yadra. Nepreryvnyi energeticheskii spektr mozhno predstavit' kak nabor beskonechno bol'shogo chisla diskretnyh sostoyanii, mezhdu k-rymi energetich. zazory beskonechno maly.

Sostoyanie, k-romu sootvetstvuet naimen'shaya energiya, vozmozhnaya dlya dannoi sistemy, naz. osnovnym: vse ostal'nye sostoyaniya naz. vozbuzhdennymi. Chasto byvaet udobnym pol'zovat'sya uslovnoi shkaloi energii, v k-roi energiya osn. sostoyaniya schitaetsya nachalom otscheta, t.e. polagaetsya ravnoi nulyu (v etoi uslovnoi shkale vsyudu v dal'neishem energiya oboznachaetsya bukvoi E). Esli sistema, nahodyas' v sostoyanii n (prichem indeks n=1 prisvaivaetsya osn. sostoyaniyu), obladaet energiei En, to govoryat, chto sistema nahoditsya na energeticheskom urovne En. Chislo n, numeruyushee U.e., naz. kvantovym chislom. V obshem sluchae kazhdyi U.e. mozhet harakterizovat'sya ne odnim kvantovym chislom, a ih sovokupnost'yu; togda indeks n oznachaet sovokupnost' etih kvantovyh chisel.

Esli sostoyaniyam n1, n2, n3,..., nk sootvetstvuet odna i ta zhe energiya, t.e. odin U.e., to etot uroven' nazyvaetsya vyrozhdennym, a chislo k - kratnost'yu vyrozhdeniya.

Pri lyubyh prevrasheniyah zamknutoi sistemy (a takzhe sistemy v postoyannom vnesh. pole) ee polnaya energiya energiya sohranyaetsya neizmennoi. Poetomu energiya otnositsya k t.n. sohranyayushimsya velichinam. Zakon sohraneniya energii sleduet iz odnorodnosti vremeni.

Polnyi moment kolichestva dvizheniya.
Eta velichina yavl. vektornoi i poluchaetsya slozheniem MKD vseh chastic, vhodyashih v sistemu. Kazhdaya chastica obladaet kak sobstv. MKD - spinom, tak i orbital'nym momentom, obuslovlennym dvizheniem chasticy otnositel'no obshego centra mass sistemy. Kvantovanie MKD privodit k tomu, chto ego abs. velichina J prinimaet strogo opredelennye znacheniya: $J=\hbar\sqrt{j(j+1)}$, gde j - kvantovoe chislo, k-roe mozhet prinimat' neotricatel'nye celye i polucelye znacheniya (kvantovoe chislo orbital'nogo MKD vsegda celoe). Proekciya MKD na k.-l. os' naz. magn. kvantovym chislom $m_j$ i mozhet prinimat' 2j+1 znachenii: mj=j, j-1,...,-j. Esli k.-l. moment J yavl. summoi dvuh dr. momentov ${\bf J}={\bf J}_1+{\bf J}_2$, to, soglasno pravilam slozheniya momentov v kvantovoi mehanike, kvantovoe chislo j mozhet prinimat' sleduyushie znacheniya: j=|j1-j2|, |j1-j2-1|, ...., |j1+j2-1|, j1+j2, a $m_j=m_{j_1}+m_{j_2}$. Analogichno proizvoditsya summirvoanie bol'shego chisla momentov. Prinyato dlya kratkosti govorit' o MKD sistemy j, podrazumevaya pri etom moment, abs. velichina k-rogo est' $\hbar\sqrt{j(j+1)}$; o magn. kvantovom chisle govoryat prosto kak o proekcii momenta.

Pri razlichnyh prevrasheniyah sistemy, nahodyasheisya v central'no-simmetrichnom pole, polnyi MKD sohranyaetsya, t.e., kak i energiya, on otnositsya k sohranyayushimsya velichinam. Zakon sohraneniya MKD sleduet iz izotropii prostranstva. V aksial'no-simmetrichnom pole sohranyaetsya lish' proekciya polnogo MKD na os' simmetrii.

Chetnost' sostoyaniya.
V kvantovoi mehanike sostoyaniya sistemy opisyvayutsya t.n. volnovymi f-ciyami. Chetnost' harakterizuet izmenenie volnovoi f-cii sistemy pri operacii prostranstvennoi inversii, t.e. zamene znakov koordinat vseh chastic. Pri takoi operacii energiya ne izmenyaetsya, togda kak volnovaya f-ciya mozhet libo ostat'sya neizmennoi (chetnoe sostoyanie), libo izmenit' svoi znak na protivopolozhnyi (nechetnoe sostoyanie). Chetnost' P prinimaet dva znacheniya, sootvetstvenno $P=\pm 1$. Esli v sisteme deistvuyut yadernye ili el.-magn. sily, chetnost' sohranyaetsya v atomnyh, molekulyarnyh i yadernyh prevrasheniyah, t.e. eta velichina takzhe otnositsya k sohranyayushimsya velichinam. Zakon sohraneniya chetnosti yavl. sledstviem simmetrii prostranstva po otnosheniyu k zerkal'nym otrazheniyam i narushaetsya v teh processah, v k-ryh uchastvuyut slabye vzaimodeistviya.

Kvantovye perehody
- perehody sistemy iz odnogo kvantovogo sostoyaniya v drugoe. Takie perehody mogut privodit' kak k izmeneniyu energetich. sostoyaniya sistemy, tak i k ee kachestv. izmeneniya. Eto svyazanno-svyazannye, svobodno-svyazannye, svobodno-svobodnye perehody (sm. Vzaimodeistvie izlucheniya s veshestvom), napr., vozbuzhdenie, deaktivaciya, ionizaciya, dissociaciya, rekombinaciya. Eto takzhe him. i yadernye reakcii. Perehody mogut proishodit' pod deistviem izlucheniya - izluchatel'nye (ili radiaciannye) perehody ili pri stolknovenii dannoi sistemy s k.-l. dr. sistemoi ili chasticei - bezyzluchatel'nye perehody. Vazhnoi harakteristikoi kvantovogo perehoda yavl. ego veroyatnost' v ed. vremeni, pokazyvayushaya, kak chasto budet proishodit' dannyi perehod. Eta velichina izmeryaetsya v s-1. Veroyatnosti radiac. perehodov mezhdu urovnyami m i n (m>n) s izlucheniem ili poglosheniem fotona, energiya k-rogo ravna $h\nu_{mn}=E_m-E_n$, opredelyayutsya koeff. Einshteina Amn, Bmn i Bnm. Perehod s urovnya m na uroven' n mozhet proishodit' spontanno. Veroyatnost' izlucheniya fotona Bmn v etom sluchae ravna Amn. Perehody tipa $m\rightleftharpoons n$ pod deistviem izlucheniya (inducirovannye perehody) harakterizuyutsya veroyatnostyami izlucheniya fotona $R_{mn}=B_{nm} \rho_\nu$ i poglosheniya fotona $R_{nm}=B_{nm} \rho_\nu$, gde $\rho_\nu$ - plotnost' energii izlucheniya s chastotoi $\nu$.

Vozmozhnost' osushestvleniya kvantovogo perehoda s dannogo U.e. na k.-l. drugoi U.e. oznachaet, chto harakternoe sr. vremya $\Delta t$, v techenie k-rogo sistema mozhet nahoditsya na etom U.e., konechno. Ono opredelyaetsya kak velichina, obratnaya summarnoi veroyatnosti raspada dannogo urovnya, t.e. summe veroyatnostei vseh vozmozhnyh perehodov s rassmatrivaemogo urovnya na vse drugie. Dlya radiac. perehodov summarnaya veroyatnost' est' $R_m=\sum\limits_i R_{mi}$, a $\Delta t=R_m^{-1}$. Konechnost' vremeni $\Delta t$, soglasno sootnosheniyu neopredelennostei $\Delta E \cdot \Delta t \ge \hbar$, oznachaet, chto energiya urovnya ne mozhet byt' opredelena absolyutno tochno, t.e. U.e. obladaet nek-roi shirinoi. Poetomu izluchenie ili pogloshenie fotonov pri kvantovom perehode $m\to n$ proishodit ne na strogo opredelennoi chastote $\nu_{mn}$, a vnutri nek-rogo chastotnogo intervala, lezhashego v okrestnosti znacheniya $\nu_{mn}$. Rapredelenie intensivnosti vnutri etogo intervala zadaetsya profilem spektral'noi linii $\varphi(\nu)$, opredelyayushim veroyatnost' togo, chto chastota fotona, ispushennogo ili pogloshennogo pri dannom perehode, ravna $\nu$:
$\varphi(\nu)={\Delta \nu\over {\pi}}\cdot {1 \over {(\nu-\nu_{mn})^2+(\Delta \nu)^2}}$ (1)
gde $\Delta \nu=(R_m-R_n)/4\pi$ - polushirina profilya linii. Esli ushirenie U.e. i spektral'nyh linii vyzvano tol'ko spontannymi perehodami, to takoe ushirenie naz. estestvennym. Esli v ushirenii opredelennuyu rol' igrayut stolknoveniya sistemy s dr. chasticami, to ushirenie imeet kombinirvoannyi harakter i velichina $\Delta \nu$ dolzhna byt' zamenena summoi $\Delta \nu + (\Delta \nu)_C$, gde $(\Delta \nu)_C$ vychislyaetsya podobno $\Delta \nu$, no radiac. veroyatnosti perehodov dolzhny byt' zameneny stolknovitel'nymi veroyatnostyami.

Perehody v kvantovyh sistemah podchinyayutsya opredelennym pravilam otbora, t.e. pravilam, ustanavlivayushim, kak mogut menyat'sya pri perehode kvantovye chisla, harakterizuyushie sostoyanie sistemy (MKD, chetnost' i t.p.). Naibolee prosto pravila otbora formuliruyutsya dlya radiac. perehodov. V etom sluchae oni opredelyayutsya sv-vami nachal'nogo i konechnogo sostoyanii, a takzhe kvantovymi harakteristikami izluchaemogo ili pogloshaemogo fotona, v chastnosti ego MKD i chetnost'yu. Naibol'shei veroyatnost'yu obladayut t.n. elektricheskie dipol'nye perehody. Eti perehody osushestvlyayutsya mezhdu urovnyami protivopolozhnoi chetnosti, polnye MKD k-ryh otlichayutsya na velichinu $\Delta J =0, \pm 1$ (perehod $J=0 \to 0$ nevozmozhen). V ramkah slozhivsheisya terminologii eti perehody naz. razreshennymi. Vse ostal'nye tipy perehodov (magnitnyi dipol'nyi, elektricheskii kvadrupol'nyi i t.p.) naz. zapreshennymi. Smysl etogo termina sostoit lish' v tom, chto ih veroyatnosti okazyvayutsya mnogo men'she veroyatnostei dipol'nyh elektricheskih perehodov. Odnako oni ne yavl. zapreshennymi absolyutno.

2. Energeticheskie urovni atomov

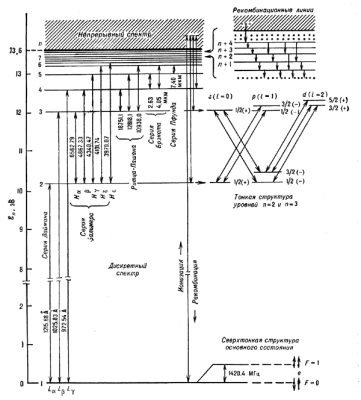
Atom vodoroda.
Prosteishim atomom (A) yavl. A vodoroda, sostoyashii iz protona i E, svyazannyh gl. obr. elektrostaticheskim kulonovskim vzaimodeistviem. Kachestvenno podoben A vodoroda vodorodopodobnyi ion, t.e. sistema, sostoyashaya iz yadra s zaryadom Z i odnogo E. Shema U.e. A vodoroda pokazana na ris. 1. Energiya urovnei v nerelyativistskom priblizhenii daetsya vyrazheniem:
$E_n=R_H \left( 1- {1 \over {n^2}} \right)$ , (2)
gde $R_H=13,6058$ eV - Ridberga postoyannaya dlya A vodoroda, velichina n naz. glavnym kvantovym chislom i mozhet prinimat' znacheniya n=1, 2, 3, ...., $\infty$. U.e., sootvetstvuyushie razlichnym n, pokazany v levoi chasti risunka; pri uvelichenii n oni sgushayutsya k granice ionizacii 13,6 eV. Perehody mezhdu U.e. s razlichnymi znacheniyami n privodyat k obrazovaniyu spketra, sostoyashego iz otchetlivo vyrazhennyh spektral'nyh serii (dlya serii Breketa i Pfunda dliny voln na ris. dany v mikrometrah, dlya ostal'nyh - v angstremah). Nablyudenie i izluchenie etih linii igraet vazhnuyu rol' v issledovanii atmosfer zvezd. V rezul'tate sushestvennogo uluchsheniya chuvstvitel'nosti astronomich. priemnikov IK-izlucheniya udalos' nablyudat' linii, prinadlezhashie seriyam Breketa i Pfunda, k-rye obrazuyutsya v kompaktnyh zonah HII, okruzhayushih ochen' molodye zvezdy.
Ris. 1. Shema energeticheskih urovnei atoma vodoroda.
Dliny voln dany v \AA. Dlya serii Breketa i Pfunda v mkm.

Na ris. 1 pokazany takzhe perehody mezhdu urovnyami, lezhashimi v diskretnom i nepreryvnom spektre: svobodno-svyazannye perehody - rekombinaciya i obratnye svyazanno-svobodnye perehody - ionizaciya.

Rekombinaciya atomov na U.e. s bol'shmim znacheniyami n i posleduyushie kaskadnye perehody na nizhelezhashie urovni privodyat k obrazovaniyu linii, poluchivshih nazvanie rekombinacionnyh (sm. Rekombinacionnye radiolinii). Nek-rye iz takih perehodov pokazany v verhnei pravoi chasti ris. 1.

Elektron v A v obshem sluchae obladaet orbital'nym MKD l, k-ryi mozhet prinimat' celochislennye znacheniya v intervale $0 \le l \le n-1$. V atomnoi spektroskopii prinyato oboznachat' sostoyaniya, sootvetstvuyushie razlichnym znacheniyam l=0, 1, 2, ..., bukvami latinskogo alfavita s, p, d, f, g (i dalee v poryadke bukv latinskogo alfavita). Naprimer, sostoyanie n=1, l=0 oboznachaetsya kak 1s, sostoyanie n=3, l=2 - 3d. Tak, k U.e. n=1 otnositsya odno sostoyanie 1s, k U.e. n=2 - sostoyaniya 2s, 2p, k U.e. n=3 - sostoyaniya 3s, 3p, 3d, i t.d.

Soglasno (2), v nerelyativistskom priblizhenii energiya urovnya s kvantovym chislom n ne zavisit ot l i ml (ml - proekciya orbital'nogo MKD na k.-l. os'). T.o., v etom priblizhenii uroven' n okazyvaetsya vyrozhdennym. Kratnost' etogo vyrozhdeniya est' n2. Nezavisimost' energii ot ml legko ob'yasnyaetsya tem, chto v pole, obladayushim sferich. simmetriei (takovo kulonovskoe pole yadra), vse napravleniya v prostranstve ravnopravny, i poetomu energiya ne mozhet zaviset' ot orientacii MKD v prostranstve. Chto kasaetsya nezavisimosti energii ot l, to ona svyazana tol'ko so specifikoi kulonovskogo vzaimodeistviya mezhdu yadrom i E. Vyrozhdenie po l snimaetsya, kogda pri raschete energii atomnogo U.e. uchityvayutsya takie relyativistskie popravki, kak zavisimost' massy E ot skorosti (sm. Relyativistskie chasticy) i spin-orbital'noe vzaimodeistvie, t.e. vzaimodeistvie, zavisyashee ot velichin i vzaimnoi orientacii orbital'nogo i spinovogo MKD E. Uchet etih popravok daet sleduyushuyu f-lu dlya energii urovnya:
$E_{nlj}=R_H\left(1- {1\over {n^2}} \left[1- {\alpha^2 \over n} \left( {3\over {4n}} - {1\over {j+1/2}}\right) \right] \right)$ , (3)
gde $\alpha=e^2/\hbar c$=1/137 - postoyannaya tonkoi struktury, j - polnyi MKD, slagayushiisya iz orbital'nogo i spinovogo MKD. Soglasno pravilam slozheniya MKD, j mozhet prinimat' dva znacheniya: $j=l\pm 1/2$. T.o., kazhdoe sostoyanie s $l \ne 0$ rassheplyaetsya na dva urovnya s razlichnymi energiyami. Eti rasshepleniya mnogo men'she, chem rasstoyaniya mezhdu U.e. s razlichnymi znacheniyami n, i naz. tonkimi rasshepleniyami (tonkaya struktura). Tonkaya struktura U.e. s n=2 i n=3 v A vodoroda pokazana na ris. 1. Sprava ot kazhdogo U.e. ukazany znacheniya j i chetnost' urovnya, a strelkami pokazany perehody, otvetstvennye za liniyu H$_\alpha$ (samaya dlinnovolnovaya liniya v serii Bal'mera). Analogichnaya struktura imeetsya u vseh urovnei n >0, l >0. Velichina tonkogo rasshepleniya ubyvaet s rostom n kak 1/n3. Poetomu ono osobenno vazhno dlya nizhnih sostoyanii.

Rassheplenie eshe men'shei velichiny (sverhtonkoe rassheplenie) obyazano vzaimodeistviyu magn. momentov yadra i E. Eto rassheplenie pokazano na ris. 1 dlya osn. sostoyaniya A vodoroda. Magn. momenty E i yadra (v dannom sluchae protona) proporcional'ny ih spinam. Poskol'ku spin protona I=1/2, to polnyi MKD A v osn. sostoyanii (pri uchete yadernogo spina on obychno oboznachaetsya bukvoi F) mozhet prinimat' dva znacheniya: F=1 (spiny e i p parallel'ny) i F=0 (spiny e i p antiparallel'ny). Energii etih sverhtonkih podurovnei razlichny, a perehody mezhdu nimi privodyat k obrazovaniyu radiolinii vodoroda 21 sm.

Mnogoelektronnye atomy.
V mnogoelektronnyh atomah pomimo kulonovskogo vzaimodeistviya kazhdogo E s yadrom imeyutsya takzhe vzaimodeistviya E drug s drugom i obmennoe vzaimodeistvie, svyazannoe s nerazlichimost'yu E pri ih kvantovomehanicheskom opisanii. Dvizhenie kazhdogo iz E mozhno rassmatrivat' proishodyashim v nek-rom usrednennom pole, sozdavaemom yadrom i vsemi dr. E. Dlya priblizhennogo opisaniya mozhno ispol'zovat' kvantovye chisla n i l, odnako v dannom sluchae vyrozhdenie po l otsutstvuet dazhe v nerelyativistskom priblizhenii. Tem ne menee kazhdyi U.e. s dannymi n i l eshe ostaetsya vyrozhdennym po proekcii orbital'nogo i spinovogo MKD. Kratnost' etogo vyrozhdeniya ravna (2s+1)(2l+1)=2(2l+1), t.k. dlya elektrona s=1/2. Soglasno principu Pauli, v kazhdom iz etih sostoyanii mozhet nahoditsya tol'ko po odnomu E. Poetomu maksimal'no vozmozhnoe chislo sostoyanii v A s dannymi n i l ravno 2(2l+1) i eti sostoyaniya, nazyvaemye ekvivalentnymi, obrazuyut elektronnuyu obolochku. Elektronnaya obolochka naz. zamknutoi, esli vse vozmozhnye sostoyaniya v nei zapolneny. Sovokupnost' 2n2 sostoyanii s odnim i tem zhe n, no raznymi l naz. elektronnym sloem (napr., K-sloi, soderzhashii 2 E pri n=1, L-sloi, soderzhashii 8 E pri n=2, M-sloi, soderzhashii 18 E pri n=3). zakonomernostyami v posledovatel'nom zapolnenii elektronnyh obolochek ob'yasnyaetsya periodichnost' izmeneniya sv-v elementov. Posledovatel'nost', v k-roi vozrastayut energii E s zadannymi n i l, sleduyushaya: 1s, 2s, 2p, 3s, 3p, 3d, ... i t.d. (zdes' bukvy lat. alfavita, kak i ranee, otnosyatsya k znacheniyam orbital'nogo MKD l=0, 1, 2, ...). Sovokupnost' vseh atomnyh E, nahodyashihsya v opredelennyh energetich. sostoyaniyah, naz. elektronnoi konfiguraciei A. Dlya ee opisaniya ukazyvayut, kakim obrazom pri vozrastanii n E rapredelyayutsya po obolochkam. Dlya etogo perechislyayut vse elektronnye obolochki, v k-ryh est' E, a imenno: ukazyvayut glavnoe kvantovoe chislo n, lat. bukvuYu sootvetstvuyushuyu znacheniyu orbital'nogo MKD l, i (sverhu sprava ot etoi bukvy) chislo E v dannoi obolochke. Napr., konfiguraciya 1s2 2s2 2p2 osn. sostoyaniya A ugleroda oznachaet, chto v pervom elektronnom sloe nahoditsya dva s-elektrona, vo vtorom sloe nahoditsya dva E v s-obolochke i dva E v p-obolochke.

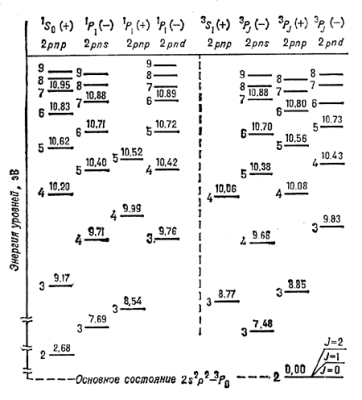
Elektronnaya konfiguraciya opredelyaet energiyu A lish' priblizhenno. Dlya dal'neishego utochneniya etoi velichiny neobhodimo znat', kakoi tip svyazi MKD E realizuetsya v A. Opyt pokazyvaet, chto v legkih A, gde relyativistskie effekty sravnitel'no maly, realizuetsya t.n. LS-tip svyazi (chasto ee nazyvayut takzhe normal'noi ili svyaz'yu Rassela-Saundersa). V etom sluchae vse orbital'nye MKD E skladyvayutsya v orbital'nyi MKD L , a vse elektronnye spiny summiruyutsya v moment S. Momenty L i S skladyvayutsya v polnyi MKD elektronnoi obolochki J. V tyazhelyh A, gde relyativistskie effekty sushestvenny (spin-orbital'noe i spin-spinovoe vzaimodeistviya), realizuetsya t.n. jj-svyaz', a imenno: orbital'nyi j i spinovoi s MKD kazhdogo E skladyvayutsya v polnyi MKD elektronnoi obolochki A J. Sleduet otmetit', chto, voobshe govorya, chistyh tipov svyazi v real'nyh A ne byvaet i ukazannye tipy - eto predel'nye sluchai, s horoshei tochnost'yu realizuemye dlya legkih (LS) i tyazhelyh (jj) A. V astrofizich. prilozheniyah naibol'shii interes predstavlyaet rassmotrenie U.e. v A s LS-svyaz'yu momentov v elektronnyh obolochkah. Poetomu ona opisana zdes' bolee podrobno (o jj-svyazi sm. razdel 4 i lit. pri stat'e).

Ris. 2. Uchastok energeticheskogo spektra
atoma ugleroda. Chisla, stoyashie nad chertoi,
k-raya oboznachaet uroven', dayut ego energiyu v eV.
Glavnye kvantovye chisla n ukazany sleva ot
oboznacheniya urovnei.
Esli v elektronnoi obolochke A realizuetsya LS-svyaz', to U.e., sootvetstvuyushii dannoi elektronnoi konfiguracii, rassheplyaetsya na celyi ryad urovnei, harakterizuemyh znacheniyami L i S, naz. spektral'nymi termami. Dlya oboznacheniya termov obychno ispol'zuyutsya zaglavnye bukvy lat. alfavita. Znacheniya L=0, 1, 2, ... sootvetstvuyut termy S, P, D, F, G i t.d. Vmesto znacheniya spina S ukazyvayut mul'tipletnost' terma, ravnuyu 2S+1, k-raya stavitsya sleva vverhu u znaka terma. Esli mul'tipletnost' ravna 1, term naz. singletnym, 2 - dubletnym, 3 - tripletnym i t.d. Empiricheski ustanovlenoYu chto naimen'shei energiei obladaet term s naibol'shim vozmozhnym dlya dannoi elektronnoi konfiguracii znacheniem S i naibol'shim (vozmozhnym pri etom S) znacheniem L (pravilo Hunda). Relyativistskie effekty, i prezhde vsego spin-oryuital'noe vzaimodeistvie, privodyat k rasshepleniyu terma s dannymi L i S na ryad urovnei, sootvetstvuyushih razlichnym vozmozhnym znacheniyam J polnogo MKD ($|L-S| \le J \le L+S$). Eto rassheplenie naz. tonkim ili mul'tipletnym. Dlya harakteristiki sostoyaniya pri nalichii tonkoi struktury naryadu s elektronnoi konfiguraciei, termom i mul'tipletnost'yu ukazyvayut takzhe znachenie polnogo MKD J, k-roe stavitsya sprava vnizu u oboznacheniya terma. Napr., osn. sostoyanie A ugleroda est' 1s2 2s2 2p2 - 3P0, t.e. elektronnaya konfiguraciya osn. sostoyaniya A ugleroda est' 1s2 2s2 2p2, polnyi orbital'nyi MKD L=1, polnyi spinovyi MKD S=1, polnyi MKD elektronnoi obolochki J=0. Na ris. 2 priveden uchastok energetich. spektra A ugleroda. V verhnei chasti ris. termy, mul'tipletnosti, znacheniya polnyh momentov J, chetnosti i elektronnye konfiguracii. Vse urovni razbivayutsya na dve gruppy s razlichnymi mul'tipletnostyami: singlety (S=0) i triplety (S=1). Radiac. perehody mezhdu etimi dvumya gruppami urovnei (interkombinacionnye perehody) yavl. zapreshennymi. Dlya terma 3P0 pokazana tonkaya struktura.

V mezhzvezdnoi srede nablyudaetsya bol'shoe kolichestvo UF- i optich. linii, sootvetstsvuyushih razlichnym perehodam v mnogoelektronnyh A i ionah. Ryad perehodov iz vozbuzhdennyh sostoyanii v nizhnie elektronnye sloi (K-, L-sloi) v tyazhelyh A privodit k izlucheniyu v rentg. oblasti spektra.

Nalichie tonkoi struktury u mnogih A igraet bol'shuyu rol' v astrofizich. yavleniyah. Napr., v A ugleroda i kisloroda urovni tonkoi struktury legko vozbuzhdayutsya pri stolknoveniyah etih A s dr. chasticami v oblakah mezhzvezdnogo gaza. Izluchatel'naya deaktivaciya urovnei tonkoi struktury, soprovozhdayushayasya izlucheniem fotonov, sposobstvuet vyvodu teplovoi energii iz gazovo-pylevyh oblakov. Etot process mozhet okazat'sya osobenno vazhnym na nachal'nom etape zvezdoobrazovaniya pri uplotnenii gazovyh kondensacii, v k-ryh nachinaetsya gravitac. szhatie protozvezd. Perehody mezhdu urovnyami tonkoi struktcry A i ionov kisloroda, ugleroda, sery, argona, neona i dr. nablyudayutsya v mezhzvezdnoi srede v IK-diapazone.

Kak i v A vodoroda, v mnogoelektronnyh A imeyutsya sverhtonkie rasshepleniya U.e. Perehody mezhdu urovnyami sverhtonkoi struktury popadayut v radiodiapazon. Napr., dlina volny takogo perehoda v A azota ravna 11,5 m. Predprinimayutsya poiski etoi linii v mezhzvezdnoi srede.

Rekombinaciya mnogoelektronnyh A na U.e. s bol'shimi znacheniyami n i posleduyushie izluchatel'nye perehody mezhdu etimi urovnyami privodyat k obrazovaniyu rekombinac. linii. Iz-za togo chto massy yader slozhnyh A bol'she, chem massa yadra A vodoroda, rekombinac. linii etih A slegka sdvinuty otnositel'no sootvetstsvuyushih vodorodnyh linii v korotkovolnovuyu oblast' spektra.

3. Energeticheskie urovni molekul

Osnovnye tipy dvizhenii v molekulah.
V obshem sluchae v molekule (M) imeetsya tri tipa dvizhenii: elektronnoe, kolebatel'noe i vrashatel'noe. Dvizhenie kazhdogo E v M proishodit v elektricheskom pole atomnyh yader i v pole vseh drugih E. Tak zhe kak i v atomah v M elektrony obrazuyut vpolne opredelennye konfiguracii, a elektronnaya energiya $E_{el}$ kvantuetsya. Sostoyanie M, sootvetstvuyushee opredelennomu znacheniyu $E_{el}$, naz. elektronnym sostoyaniem. V otlichie ot atomov, v M $E_{el}$ v kazhdom elektronnom sostoyanii ne yavl. opredelennoi postoyannoi velichinoi, no zavisit ot mezh'yadernyh rasstoyanii (dlin svyazi) i uglov mezhdu nimi (valentnyh uglov). Eta funkcional'naya zavisimost' naz. poverhnost'yu potencial'noi energii (ili krivoi potencial'noi energii dlya dvuh atomnoi M). Poverhnost' potencial'noi energii, sootvetstvuyushaya svyazannomu sostoyaniyu M, imeet minimum pri nekotoryh znacheniyah dlin svyazi i valentnyh uglov - eti znacheniya naz. ravnovesnymi. Klassifikaciya elektronnyh sostoyanii mnogoatomnyh M provoditsya metodami teorii grupp.

Naibolee prostymi sistemami s tochki zreniya klassifikacii energeticheskih sostoyanii yavl. lineinye, ili dvuhatomnye M. V lineinoi M elektricheskoe pole, deistvuyushee na E, obladaet aksial'noi simmetriei. Poetomu kazhdoe elektronnoe sostoyanie harakterizuetsya opredelennym znacheniem proekcii summarnogo orbital'nogo MKD vseh E na os' M. Eta velichina oboznachaetsya $\Lambda$. Razlichnym znacheniyam abs. velichiny $\Lambda$ sootvetstvuyut razlichnye elektronnye sostoyaniya, ili termy, k-rye oboznachayutsya bol'shimi bukvami grech. alfavita: $\Lambda=0 - \Sigma$-sostoyanie, $\Lambda=1 - \Pi$-sostoyanie, $\Lambda=2 - \Delta$-sostoyanie i t.d. Elektronnye sostoyaniya harakterizuyutsya takzhe summarnym spinom vseh elektronov S. Spin-orbital'noe vzaimodeistvie privodit k rasshepleniyu elektronnogo terma s dannym S na 2S+1 blizko lezhashih U.e. (tonkaya struktura). Chislo 2S+1 naz. mul'tipletnost'yu elektronnogo terma i stavitsya sleva vverhu u grech. bukvy, ukazyvayushei znachenie $\Lambda$, napr., $^2\Pi$, $^3\Sigma$. Opyt pokazyvaet, chto osn. elektronnoe sostoyanie bol'shinstva M est' $^1\Sigma$-sostoyanie. Sushestvuet, odnako, ryad M, v t.ch. takie mezhzvezdnye M kak OH, NO, CH, osn. sostoyanie k-ryh harakterizuetsya otlichnymi ot nulya znacheniyami L ili/i S.

Pri $\Lambda\ne 0$ vozmozhny dva sostoyaniya s odinakovoi energiei, otlichayushiesya znakom proekcii orbial'nogo MKD na os' M ($\pm\Lambda$). T.o., vse sostoyaniya s $\Lambda\ne 0$ dvuhkratno vyrozhdeny. $\Sigma$-sostoyaniya ne vyrozhdeny. Razlichayut $\Sigma^+$- i $\Sigma^-$-sostoyaniya. Znaki $\pm$ oboznachayut chetnost' sostoyaniya po otnosheniyu k operacii otrazheniya v ploskosti, soderzhashei os' M. Esli M obladaet centrom simmetrii (napr., H2, O2, CO2, H2C2), to poyavlyaetsya dopolnit. kvantovoe chislo - chetnost' po otnosheniyu k inversii prostranstva. Chetnye sostoyaniya oboznachayut indeksom $g (\Sigma_g, \Pi_g,...)$, a nechetnye - indeskom $u (\Sigma_u, \Pi_u,...)$.

Osn. sv-va krivyh potencial'noi energii illyustriruyutsya ris. 3, gde pokazany takie krivye dlya treh elektronnyh sostoyanii molekuly H2 - $^1\Sigma^+_g, ^3\Sigma^+_u, ^1\Sigma^+_u$ (dlya naglyadnosti masshtaby po osyam energii i mezh'yadernyh rasstoyanii ne vyderzhany tochno). Krivye dlya $^1\Sigma^+_g-, ^1\Sigma^+_u-$sostoyanii imeyut minimumy pri ravnovesnyh mezh'yadernyh rasstoyaniyah R=Re i sootvetstvuyut svyazannym sostoyaniyam M. Pri $R\to \infty$ oba atoma vodoroda svobodny i Eel ravna summe energii oboih atomov. Velichina $E_{\mbox{el}}(\infty)$ naz. granicei dissociacii. Pri sblizhenii atomov obrazuetsya ustoichivaya M. Kogda R < Re, potencial'naya energiya rastet, t.k. nachinaet skazyvat'sya kulonovskoe ottalkivanie yader. Raznost' energii $D_c=E_{el}(\infty)-E_{el}(R_e)$ naz. energiei dissociacii. Krivaya potencial'noi energii dlya sostoyaniya $^3\Sigma^+_u$ ne imeet minimuma, t.e. eto sostoyanie ne yavl. svyazannym. Sblizhayushiesya atomy s takim naborom kvantovyh chisel posle stolknoveniya rashodyatsya, i M ne obrazuetsya.

Kolebaniya molekuly.
Iz vida potencial'noi krivoi dlya svyazannogo sostoyaniya M yasno, chto pri umen'shenii ili uvelichenii mezh'yadernogo rasstoyaniya otnositel'no ravnovesnogo poyavlyaetsya sila, stremyashayasya vernut' yadra v polozhenie ravnovesiya, R=Re. Eta sila privodit k vozniknoveniyu kolebatel'nogo dvizheniya yader.

V mnogoatomnyh M kolebatel'nye dvizheniya yader zaklyuchayutsya v periodicheskom izmenenii dlin svyazei i valentnyh uglov otnositel'no ih ravnovesnyh znachenii. Kolebatel'noe dvizhenie kvantuetsya, chto privodit k vozniknoveniyu diskretnogo kolebatel'nogo energeticheskogo spektra. Kazhdyi kolebatel'nyi U.e. dvuhatomnoi M (chislo kolebatel'nyh stepenei svobody i=1 - odnomernoe dvizhenie) harakterizuetsya kvantovym chislom v, a energiya urovnya ravna:
$E_{\mbox{kol}}=h\nu \left(v+{1\over 2} \right) \left[1-x \left(v+{1\over 2} \right) \right]$ , v=0, 1, 2, ..., (4)
gde $\nu$ i x - osn. chastota i postoyannaya angarmonizma; eti konstanty otlichayutsya dlya razlichnyh elektronnyh sostoyanii. Mnogoatomnye M, sostoyashie iz N atomov imeyut chislo kolebatel'nyh stepenei svobody $i\ge 3$ i=3N-5 dlya lineinyh M i i=3N-6 dlya nelineinyh). Kazhdyi kolebatel'nyi U.e. v etom sluchae harakterizuetsya naborom kolebatel'nyh kvantovyh chisel (v1, v2,..., vi), a energiya Ekol opredelyaetsya priblizhennym vyrazheniem:
$E_{\mbox{kol}}\approx \Sigma^i_{\mu=1} h\nu_\mu \left(v_\mu+{1\over 2} \right),\quad v_\mu=0, 1, 2, ..., $ (5)
gde $\nu_\mu$ - osn. chastoty (inogda ih naz. chastotami normal'nyh kolebanii). Urovni kolebatel'noi energii dlya M vysokoi stepeni simmterii mogut byt' dvazhdy i trizhdy vyrozhennymi.

Polozhenie kolebatel'nyh U.e. dvuhatomnoi M pokazany na ris. 3 gorizontal'nymi liniyami u pravyh vetvei krivyh potencial'noi energii Ekol(R). Kolebatel'nye U.e. sgushayutsya k granice dissociacii $E_{\mbox{el}}(\infty)$, no ih chislo konechno v otlichie ot atomnyh urovnei, dlya k-ryh glavnoe kvantovoe chislo n mozhet prinimat' kakie ugodno bol'shie znacheniya. Vyshe granicy dissociacii lezhit nepreryvnyi energeticheskii spektr, sootvetstvuyushii dissociirovannomu sostoyaniyu: polnaya energiya svobodnyh atomov mozhet prinimat' proizvol'nye znacheniya.

Vrashenie molekul.
Vrashatel'noe dvizhenie M kak celogo mozhno priblizhenno rassmatrivat' kak povoroty tvordogo tela vokrug nek-roi osi. Vrashat. dvizhenie kvantuetsya, chto privodit k vozniknoveniyu diskretnogo vrashatel'nogo energeticheskogo spektra. Kazhdyi vrashat. U.e. harakterizuetsya vrashat. energiei Evr, vrashat. MKD J, chetnost'yu P i nekotorymi dopolnitel'nymi kvantovymi chislami, k-rye chasto okazyvayutsya neobhodimymi dlya opisaniya vrasheniya nelineinyh M.

V obshem sluchae mnogoatomnaya M imeet tri glavnyh momenta inercii I1, I2, I3, otnositel'no treh vzaimno perpendikulyarnyh osei, svyazannyh s M. Dlya lineinoi M $I_1=I_2, I_3=0$ (os' 3 v dannom sluchae sovpadaet s os'yu M). Vrashenie takoi M proishodit vokrug osi, perpendikulyarnoi osi M. Vrashat. energiya priblizhenno opredelyaetsya f-loi:
$E_{\mbox{vr}} \approx {\hbar^2\over {2I_1}}\; J(J+1), \quad J=0, 1, 2,...$ (6)
Etoi zhe f-loi opredelyaetsya energiya urovnei M tipa sferich. volchka, u k-roi I1=I2=I3 (napr., CH4, CF4). Esli $I_1=I_2\ne I_3$, to M otnositsya k tipu simmetrichnyh volchkov (napr., NH3, CH3CN). Ee U.e. harakterizuyutsya ne tol'ko znacheniyami vrashat. MKD J, no i dopolnitel'nym kvantovym chislom - proekciei J na os' simmetrii M. Eta velichina obychno oboznachaetsya bukvoi K. Energiya vrashat. U.e. v etom sluchae:
$E_{\mbox{vr}} \approx {\hbar^2\over {2I_1}}\; J(J+1) + {\hbar^2\over 2} \left( {1\over{I_3}} - {1\over{I_1}}\right) K^2 , \quad K=0, 1, 2,..., J$ . (7)
Esli zhe vse tri momenta inercii razlichny, M otnositsya k tipu asimmetrichnyh volchkov (napr., H2O, H2CO). Dlya harakteristiki ee vrashat. U.e. trebuetsya zadanie dvuh dopolnitel'nyh kvantovyh chisel, energiya vrashat. urovnei ne mozhet byt' vyrazhena prostymi f-lami tipa (6) ili (7) i rasschityvaetsya spec. metodami.

Vrashat. U.e. dvuhatomnoi M v $^1\Sigma^+$-sostoyaniyah pokazany na ris. 3 dlya dvuh kolebatel'nyh sostoyanii terma $^1\Sigma^+_g$ i treh kolebatel'nyh sostoyanii terma $^1\Sigma^+_u$. Analogichnaya vrashat. struktura (ili polosa) imeetsya u vseh h kolebatel'nyh sostoyanii. Energiya vrashat. urovnei otschityvaetsya ot polozheniya h kolebatel'nogo urovnya, k-romu prinadlezhit dannaya vrashat. polosa. Esli M imeet tozhdestvennye yadra (kak, napr., H2), eto privodit k opredelennym ogranicheniyam na sushestvovaniya vrashat. U.e. s razlichnymi znacheniyami J. V M vodoroda oba yadra (protony) imeyut spiny 1/2. Polnyi yadernyi spin mozhet prinimat' dva znacheniya: I=0 (paravodorod) i I=1 (ortovodorod). V etom sluchae, kak sleduet iz kvantovomehanich. rassmotreniya, vse vrashat. U.e. s chetnymi J v $^1\Sigma^+_g$-sostoyanii otnosyatsya k paravodorodu, a v $^1\Sigma^+_u$-sostoyanii - k ortovodorodu. Naoborot, urovni s nechetnymi J v $^1\Sigma^+_g$-sostoyanii otnosyatsya k ortovodorodu, a v $^1\Sigma^+_u$-sostoyanii - k paravodorodu. Chetnosti vrashat. sostoyanii na ris. 3 ukazany ryadom so znacheniyami J.

Polnaya energiya molekuly opredelyaetsya priblizhenno kak summa vseh vidov energii:
$E_{\mbox{mol}}\approx E_{\mbox{el}} + E_{\mbox{kol}} + E_{\mbox{vr}}$ . (8)
Prichem, kak pravilo, vypolnyayutsya neravenstva
$E_{\mbox{el}} \gg E_{\mbox{kol}} \gg E_{\mbox{vr}}$ , i
$E_{\mbox{el}}/E_{\mbox{kol}} \approx E_{\mbox{kol}} /E_{\mbox{vr}} \approx \sqrt{m_e/m_p}$ , (9)
gde mp - massa protona.

Tipy perehodov v molekulah.
V sootvetstvii so strukturoi energetich. sostoyanii v M razlichayut tri osn. tipa kvantovyh perehodov (zdes' kosnemsya tol'ko radiac. perehodov).

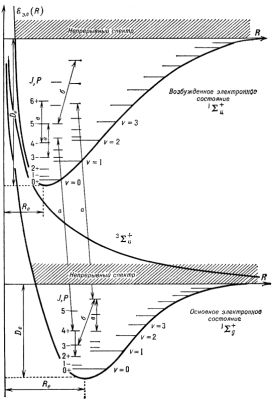
Ris. 3. Shematicheskoe izobrazhenie struktury treh elektronnyh
sostoyanii orto- i paramolekul H2. Dlya svyazannyh elektronnyh
sostoyanii $^1\Sigma^+_g$ i $^1\Sigma^+_u$ oboznacheny polozheniya
kolebatel'nyh (v=0, 1, 2, ...) i vrashatel'nyh (J=0, 1, 2, ...) urovnei
energii, a takzhe ih chetnosti P. Linii so strelkami pokazyvayut
vozmozhnye tipy perehodov: a - elektronno-kolebatel'no-vrashatel'nye,
b - kolebatel'no-vrashatel'nye, v - vrashatel'nye.
Elektronno-kolebatel'no-vrashatel'nye perehody (perehody tipa a na ris. 3).
Dliny voln etih perehodov obychno lezhat v UF- i optich. oblastyah spektra. Dlya H2 perehody tipa a otnosyatsya k serii Laimana i imeyut dliny voln ok. 1000-1100 angstrem. Oni nablyudayutsya kak v mezhzvezdnoi srede nashei Galaktiki, tak i v dr. galaktikah i, v chastnosti, v oblakah gaza, imeyushih bol'shie krasnye smesheniya. V poslednem sluchae oni mogut nablyudat'sya metodami optich. astronomii.

Kolebatel'no-vrashatel'nye perehody (perehody tipa b na ris. 3).
Ih dliny voln popadayut, kak pravilo, v IK-oblast' spektra. Napr., kolebatel'nyi perehod $v=1 \to v=0$ v H2 v osn. elektronnom sostoyanii imeet dlinu volny $\lambda\approx$2,28 mkm i nablyudaetsya v plotnyh i goryachih istochnikah svyazannyh s oblastyami zvezdoobrazovaniya.

Vrashatel'nye perehody (perehody tipa v na ris. 3).
Ih dliny voln popadayut v IK-, submillimetrovuyu i mikrovolnovuyu oblast' spektra. Napr., v mezhzvezdnoi srede nablyudayutsya vrashat. perehody H2 s dlinoi volny $\lambda\approx$28 mkm (perehod $J=2 \to J=0$), submillimetrovye perehody CO na volne $\lambda\approx$0,87 mm (perehod $J=3 \to J=2$). Radioastronomich. metodami obnaruzheno bolee 600 vrashat. linii razlichnyh mezhzvezdnyh M (sm. Molekuly v mezhzvezdnoi srede).

Nekotorye vazhnye tipy rassheplenii molekulyarnyh sostoyanii.
Pomimo osn. elektronno-kolebatel'no-vrashatel. struktury U.e. molekuly imeetsya ryad dopolnit. rassheplenii, igrayushih vazhnuyu rol' v interpretacii spektrov mezhzvezdnyh M. Kratko rassmotrim lish' nek-rye iz nih.

$\Lambda$-rassheplenie ($\Lambda$-udvoenie) obyazano vzaimodeistviyu mezhdu vrashatel'nym i elektronnym dvizheniyami v M, nahodyashihsya v $\Pi,\;\Lambda$ i t.p. sostoyaniyah, t.e. kogda proekciya orbital'nogo MKD elektronov na os' M otlichna ot nulya. Vazhnyi primer etogo tipa rasshepleniya priveden na ris. 4, gde pokazana struktura nizhnih vrashatel. U.e. mezhzvezdnoi molekuly OH. Vo vnesh. elektronnoi obolochke molekuly OH nahoditsya odin elektronYu tak chto polnyi elektronnyi spin S=1/2. Poetomu osn. sostoyanie $^2\Pi$ rasshepleno spin-orbital'nym vzaimodeistviem na dve vrashatel. polosy: $^2\Pi_{3/2}$ i $^2\Pi_{1/2}$. Nizhnii indeks u znaka terma oboznachaet summarnuyu proekciyu $\Omega$ orbital'nogo i spinovogo MKD na os' M. V dannom sluchae ($\Lambda=1, \;S=1/2$) $\Omega$ mozhet prinimat' dva znacheniya: $\Omega$=1/2 i $\Omega$=3/2.
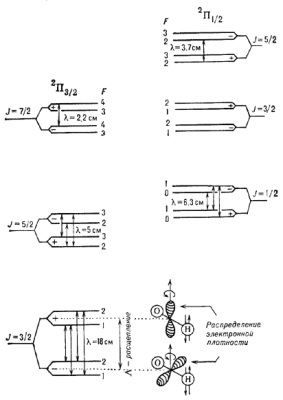
Ris. 4. Nizhnie urovni molekuly OH, $\Lambda$-rassheplenie
i sverhtonkoe rassheplenie. Sprava vnizu privedeno
raspredelenie elektronnoi plotnosti, poyasnyayushee
obrazovanie $\Lambda$-dubleta. Strelkami ukazany perehody,
k-rye nablyudayutsya v mezhzvezdnoi srede.
T.k. dlya dvuhatomnoi M vrashatel. moment perpendikulyaren molekulyarnoi osi, to polni MKD, slagayushiisya iz elektronnogo i vrashatel. MKD, ne mozhet byt' men'she $\Omega$. Poetomu dlya J vozmozhny sleduyushie nabory znachenii: J=1/2, 3/2, ... dlya polosy $^2\Pi_{1/2}$ i J=3/2, 5/2, ... dlya polosy $^2\Pi_{3/2}$. V kazhdoi vrashatel. polose vse vrashatel. U.e. udvoeny. Prichinu etogo udvoeniya kachestvenno mozhno ponyat', rassmatrivaya raspredelenie elektronnoi plotnosti v molekule OH otnositel'no osi vrasheniya. Vzaimodeistvie mezhdu vrashatel'nymi i elektronnymi dvizheniyami privodit k dvum vozmozhnym raspredeleniyam elektronnoi plotnosti, pokazannym v nizhnei chasti ris. 4. Momenty inercii, a sledovatel'no, i vrashatel. energii v etih dvuh sostoyaniyah neskol'ko otlichayutsya. Poetomu kazhdyi vrashatel. U.e. okazyvaetsya rassheplennym na dva podurovnya ($\Lambda$-udvoenie), chetnosti k-ryh protivopolozhny.

Sverhtonkoe rassheplenie.
Esli odno ili nesk. yader v M imeyut otlichnye ot nulya spiny, to kazhdyi vrashatel. U.e. rassheplyaetsya na sistemu sverhtonkih podurovnei (sverhtonkaya struktura). V etom sluchae kazhdyi U.e. harakterizuetsya polnym MKD molekuly (F). Napr., v molekule OH yadro atoma vodoroda imeet spin I=1/2, k-ryi mozhet byt' napravlen parallel'no ili antiparallel'no momentu J (strelki u atoma H na ris. 4). V sootvetstvii s pravilami slozheniya momentov F mozhet prinimat' znacheniya $J\pm$1/2, k-rye ukazany na ris. 4. Na etom ris. ukazany takezhe perehody, k-rym sootvetstvuyut radiolinii molekuly OH, nablyudaemye v mezhzvezdnoi srede.

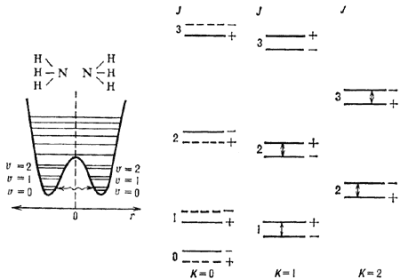
Inversionnoe rassheplenie obyazano t.n. zatormozhennym dvizheniyam v M. Eti dvizheniya svyazany s kvantovomehanicheskim tunnel'nym effektom. Na ris. 5 pokazano osn. elektronnoe sostoyanie M ammiaka NH3. Krivaya potencial'noi energii imeet dva minimuma, chto sootvetstvuet dvum vozmozhnym polozheniyam atoma azota otnositel'no ploskosti, v k-roi lezhat atomy vodoroda (r- rasstoyanie ot atoma azota do etoi ploskosti). Esli atom N nahoditsya v odnom iz minimumov krivoi potencial'noi energii , to perehod v dr. minimum v klassi. mehanike energeticheski nevozmozhen. V kvantovoi mehanike takoi perehod vozmozhen za schet tunnel'nogo effekta - chastica tunneliruet pod energetich. bar'erom, chto izobrazheno volnistoi liniei. T.o., dva minimuma potencial'noi energii okazyvayutsya svyazannymi mezhdu soboi. Soglasno kvantovoi mehanike, takaya svyaz' privodit k rasshepleniyu kazhdogo kolebatel'nogo urovnya energii, lezhashego nizhe central'nogo maksimuma, na dva podurovnya. Eto rassheplenie naz. inversionnym. Poskol'ku kazhdomu kolebatel'nomu U.e. sootvetstvuet svoya vrashatel. polosa, to dvum inversionnym podurovnyam budut sootvetstvovat' dve slegka smeshennye (na velichinu rasshepleniya) polosy, kak eto pokazano na ris. 5 sprava, gde izobrazhen uchastok vrashatel. spektra osn. kolebatel'nogo sostoyaniya ammiaka. T.k. NH3 otnositsya k M tipa simmetrichnogo volchka, to energii vrashatel. urovnei mozhno priblizhenno opredelit' po f-le (7) dlya lyubyh J i K. M ammiaka imeet tri tozhdestvennyh yadra. V silu principa Pauli nek-rye vrashatel. U.e. okazyvayutsya zapreshennymi (podobno tomu, chto imeet mesto dlya orto- i paravodoroda). Eti U.e. oboznacheny shtrihovymi liniyami. Linii, sootvetstvuyushie perehodam mezhdu inversionnymi podurovnyami (oni oboznacheny strelkami na ris. 5), popadayut v radiodiapazon vblizi chastoty 23 GGc i nablyudayutsya v mezhzvezdnoi srede.
Ris. 5. Struktura vrashatel'nyh urovnei i inversionnoe
rassheplenie v molekule ammiaka. Strelkami pokazany
perehody, nablyudaemye v mezhzvezdnoi srede.
Ih izuchenie igraet vazhnuyu rol' v issledovaniyah plotnyh i holodnyh oblakov mezhzvezdnogo gaza.

4. Energeticheskie urovni yader

Izotopicheskii spin
Pri opisanii sostoyaniya atomnyh yader, v dopolnenie k kvantovym harakteristikam, ispol'zuemym v atomnoi i molekulyarnoi spektroskopii, vvodyat ponyatie polnogo izotopicheskogo spina (izospina) T i ego proekcii MT. Eti velichiny dlya otdel'nogo nuklona (t, mt) opredelyayut ego zaryadovoe sostoyanie. Po opredeleniyu, t=1/2, a mt mozhet prinimat' dva znacheniya: mt=1/2 sootvetstvuet protonu, mt=-1/2 sootvetstvuet neitronu. Polnyi izospin yadra (Ya) T opredelyaetsya kak vektornaya summa izospinov otdel'nyh nuklonov, a ego proekciya MT=(Z-N)/2, gde Z - zaryad Ya, N - chislo neitronov v Ya. Napr., dlya pary nuklonov summarnyi izospin mozhet prinimat' dva znacheniya: T=0 i T=1. Sostoyaniya s T=0, MT=0 i T=1, MT=0 sootvetstvuyut pare np (neitron-proton). Sostoyaniya s T=1, MT=1 i T=1 MT=-1 sootvetstvuyut param pp i nn. Ot velichiny izospina v obshem sluchae zavisyat energiya svyazi i energii urovnei Ya. Kak pravilo, osn. sostoyanie Ya imeet naimen'shee iz dopustimyh znachenie izospina, t.e. Tmin =|MT|=(N-Z)/2.

Obolochechnaya model' yadra
Dlya priblizhennogo opisaniya diskretnogo energetich. spektra atomnogo Ya okazyvayutsya udobnym, tak zhe kak i dlya haraktiristiki molekulyarnyh sostoyanii, razdelit' dvizheniya v Ya na vnutrennie i kollektivnye, prichem poslednie mogut byt' dvuh tipov: kolebatel'nye, sootvetstvuyushie kolebaniyam yadernoi plotnosti ili poverhnosti Ya, i vrashatel'nye, sootvetstvuyushie vrasheniyu deformirovannomu Ya kak celogo vokrug osi, perpendikulyarnoi osi deformacii.

Vnutrennee dvizhenie nuklonov v Ya mozhet byt' priblizhenno opisano v ramkah obolochechnoi modeli, po svoim osn. predstavleniyam analogichnoi toi modeli, k-raya daet opisanie stroenie elektronnoi obolochki atoma. Obolochechnaya model' ishodit iz dopusheniya, chto v atomnom Ya kazhdyi nuklon dvizhetsya do nek-roi stepeni nezavisimo v usrednennom pole yadernyh sil, obrazovannom drugimi nuklonami. Poskol'ku radius deistviya yadernyh sil mal, eto pole ogranicheno rasstoyaniyami poryadka radiusa Ya $R\approx 1,1\cdot 10^{-13} A^{1/3}$ sm, gde A - chislo chastic v Ya (massovoe chislo). T.o., v obolochechnoi modeli sostoyanie Ya v celom opisyvaetsya perechisleniem sostoyanii otdel'nyh nuklonov. Dlya mnogih Ya sr. yadernoe pole obladaet sferich. simmetriei. Poetomu sostoyanie otdel'nogo nuklona v Ya mozhno harakterizovat' orbital'nym MKD l. Spin-orbital'noe vzaimodeistvie dlya takogo nuklona v Ya znachitel'no bol'she, chem dlya E v atome. Poetomu dlya opisaniya yadernyh sostoyanii ispol'zuetsya jj-tip svyazi MKD. Sostoyaniya nuklonov s odinakovymi l i j numeruyut v poryadke uvelicheniya energii chislom n=1, 2,... . Razlichnye sostoyaniya oboznachayut simvolami 1s1/2, 1p1/2, 1p3/2..., gde cifra pered bukvoi est' chislo n, bukvy s, p, d, f, g i t.d. imeyut tot zhe smysl, chto i v atomnoi spektroskopii, t.e. sootvestvuyut znacheniyam l=0, 1, 2, 3..., a indeks u bukvy opredelyaet velichinu polnogo MKD nuklona j.

V sostoyanii s zadannymi znacheniyami n, l, j mozhet nahodit'sya ne bolee 2j+1 nuklonov kazhdogo tipa - protonov i neitronov. T.o., nuklonnye sostoyaniya raspredelyayutsya po sleduyushim gruppam:
1s1/22 nuklona
1p3/2, 1p1/26 nuklonov
1d5/2, 1d3/2, 1d1/212 nuklonov
1f7/2, 2p3/2, 1f5/2, 2p1/2, 1g9/230 nuklonov
2d5/2, 1g7/2, 1h11/2, 2d3/2, 3s1/232 nuklona
2f7/2, 1h9/2, 1i13/2, 2f5/2, 3p3/2, 3p1/244 nuklona

Sostoyaniya v kazhdoi gruppe malo otlichayutsya po energiyam. Takie gruppy naz. nuklonnymi obolochkami. Sootvetstvenno velichinam, ukazyvayushim vozmozhnoe chislo nuklonov v kazhdoi gruppe, zaponenie k.-l. obolochki zakanchivaetsya, kogda chislo protonov ili neitronov v Ya ravno odnomu iz sleduyushih chisel: 2, 8, 20, 50, 82, 126. Eti chisla prinyat' naz. magicheskimi. Ya, soderzhashie lish' zapolnennye protonami (ili neitronami) obolochki, naz. magicheskimi yadrami. Ya magicheskie i po protonam i po neitronam naz. dvazhdy magicheskimi. Dvazhdy magicheskie Ya obladayut osoboi ustoichivost'yu po otnosheniyu k prisoedineniyu nuklona (analogichno atomam inertnyh gazov s celikom zapolnennymi elektronnymi obolochkami), a ih pervye vozbuzhdennye U.e. lezhat vyshe, chem u ostal'nyh Ya.

Bol'shaya ustoichivost' Ya s zapolnennymi protonnymi i neitronnymi obolochkami otnositel'no vozbuzhdeniya chastichno svyazana s effektom sparivaniya nuklonov.

V chetno-chetnyh Ya (t.e. v Ya s chetnym chislom proton-neitronov) pary protonov i neitronov s ravnymi, no protivopolozhno napravlennymi spinami obrazuyut v Ya sostoyaniya tipa svyazannyh. Chtoby vozbudit' Ya, t.e. perevesti odin iz nuklonov pary v bolee vysokuyu nezapolnennuyu obolochku, neobhodimo razorvat' nuklonnuyu paru, chto trebuet znachitel'noi energii. Polnyi MKD chetno-chetnogo Ya v osn. sostoyanii raven nulyu, t.k. MKD vseh nuklonov poparno kompensiruyutsya.

V naibolee prostom variante obolochechnoi modeli nechetnyh Ya predpolagaetsya, chto vse nuklony Ya za isklyucheniem nechetnogo soedinyayutsya parami i obrazuyut chetno-chetnyi ostov. Ostavshiisya nechetnyi nuklon dvizhetsya v pole etogo ostova. MKD takogo Ya raven MKD nechetnogo nuklona, a ego energetich. sostoyanie opredelyaet strukturu nizhnih U.e. Ya. Etot variant obolochechnoi modeli naz. odnochastichnoi model'yu Ya.

S rostom energii vozbuzhdeniya rasstoyaniya mezhdu U.e. bystro umen'shayutsya. Energii urovnei vozrastayut s uvelicheniem orbital'nogo MKD l. Pri zadannom l uroven' s j=l+1/2 lezhit glubzhe, chem uroven' s j=l-1/2.

Dlya harakteristiki energeticheskogo urovnya Ya obychno ukazyvayut ego energiyu, polnyi MKD J i chetnost' P. Inogda, esli eto neobhodimo, k etim kvantovym harakteristikam dobavlyayut znachenie izotopich. spina.

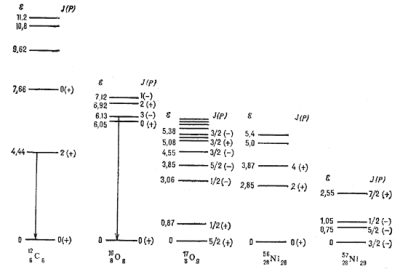
Ris. 6. Shema energeticheskih urovnei vnutrennih vozbuzhdenii yader
ugleroda, kisloroda i nikelya. Energiya E dana v MeV. Ukazany znacheniya
polnogo momenta yadra J i chetnosti sostoyaniya P. Liniyami so strelkami
pokazany perehody, k-rye nablyudalis' v solnechnyh vspyshkah.
Na ris. 6 privedeny shemy U.e. vnutr. vozbuzhdeniya yader 126C6, 168O8, 178O9, 5628Ni28, 5728Ni29. Sravnenie shem urovnei dlya izotopov 168O8, 178O9, a takzhe dlya 5628Ni28 i 5728Ni29 pokazyvaet razlichiya v energetich. strukture chetno-chetnyh i chetno-nechetnyh Ya. Linii, sootvetstvuyushie perehodam, oboznachennym strelkami dlya Ya 126C6 (4,44 MeV) i 168O8 (6,13 MeV), nablyudalis' vo vspyshkah na Solnce. Pervaya iz nih nablyudalas' takzhe v central'noi oblasti Galaktiki.

Kollektivnye dvizheniya v yadre
Dlya opisaniya etih tipov dvizhenii (oni stanovyatsya osobenno sushestvennymi dlya tyazhelyh yader) obolochechnaya model' okazyvaetsya nedostatochnoi. Poetomu byla razvita obobshennaya model' Ya, rassmatrivayushaya dvizheniya nuklonov v nezapolnennyh obolochkah v pole ostova, sostoyashego iz nuklonov, polnost'yu zapolnyayushih obolochki. Spin ostova raven nulyu. Vnesh. nuklony pri svoem dvizhenii vliyayut na formu ostova i mogut deformirovat' ego; on priobretaet formu vytyanutogo ili splyusnutogo ellipsoida vrasheniya i mozhet kolebats'ya i vrashat'sya. Eti kollektivnye dvizheniya nuklonov ostova opisyvayutsya v ramkah gidrodinamicheskoi modeli Ya.

Energiya sostoyaniya v obobshennoi modeli predstavlyaetsya summoi energii vnutrennego i kollektivnyh dvizhenii. Pod vnutrennim ponimaetsya dvizhenie nuklonov v nezapolnennyh obolochkah. V aksial'no-simmetrichnom pole deformirovannogo yadra horoshei kvantovoi harakteristikoi sostoyaniya (t.e. sohranyayusheisya velichinoi) yavlyaetsya proekciya $\Omega$ polnogo MKD etih nuklonov na os' deformacii. Polnyi MKD vrashayushegosya yadra J skladyvaetsya iz MKD nuklonov nezapolnennyh obolochek i MKD vrashayushegosya ostova, k-ryi perpendikulyaren osi deformacii. Sledovatel'no, pri zadannom $\Omega$ moment J mozhet prinimat' znacheniya $J=\Omega, \Omega+1, \Omega+1, ...$, a velichina vrashatel. energii opredelyaetsya f-loi (6). Odnako moment inercii, figuriruyushii v etoi f-le, v sluchae Ya mozhet schitat'sya nezavisimym ot J lish' pri nebol'shih znacheniyah etoi velichiny. Kogda J prevyshaet nek-ryi predel, moment inercii bystro narastaet, t.k. ravnovesnaya deformaciya uvelichivaetsya, chto privodit k perestroike struktury U.e. Intervaly mezhdu U.e. perestayut rasti v sootvetstvii s f-loi (6), i U.e. raspolagayutsya priblizitel'no ekvidistantno. Nakonec, esli Ya soobshit' ochen' bol'shoi vrashatel. MKD, ono mozhet pereiti v t.n. sverhvrashatel. sostoyanie, k-roe yavl. nestabil'nym. Iz etogo sostoyaniya Ya raspadaetsya s udaleniem neskol'kih neitronov.

Ris. 7. a - struktura vrashatel'nyh urovnei yadra 168Er,
b - struktura kolebatel'nyh urovnei yadra 188Os.
Energiya urovnei dana v keV.
Energetich. spektr Ya., opisyvaemyi f-loi (6), predstavlyaet soboi primer prosteishego spektra. Struktura vrashatel. U.e. bol'shinstva Ya imeet bolee slozhnyi harakter. Vrashatel'nye i kolebatel'nye perehody v Ya nablyudayutsya v laboratornyh eksperimentah. Nizhnie vrashatel. U.e. otstoyat ot osnovnogo na desyatki i sotni keV. Energiya kolebatel'nyh vozbuzhdenii, kak pravilo, prinimaet promezhutochnye znacheniya mezhdu energiyami vrashatel'nyh i vnutrennih vozbuzhdenii. Na ris. 7 pokazany primery vrashatel. energetich. spektra dlya yadra 168Er (etot spektr kachestvenno podoben tomu, k-ryi imeet mesto v molekulah tipa simmetrichnogo volchka) i kolebatel'nogo energetich. spektra dlya yadra 18876Os.

Vozbuzhdenie i deaktivaciya yadernyh urovnei

Vozbuzhdennoe sotstoyanie dannogo Ya chasto voznikaet v rezul'tate yadernoi reakcii k.-l. drugogo Ya s $\gamma$-fotonami, E, nuklonami, mezonami, neitrino i dr. Ya. Drugoi put' obrazovaniya vozbuzhdennogo sostoyaniya - eto pogloshenie $\gamma$-fotona ili stolknoveniya Ya s k.-l. chasticei bez posleduyushei yadernoi rekcii (napr., kulonovskoe vozbuzhdenie vrashatel'nyh urovnei Ya pri stolknovenii s zaryazhennoi chasticei). Analogichnym obrazom mozhet proishodit' deaktivaciya (raspad) vozbuzhdennyh sostoyanii. Primerom izluchatel'noi deaktivacii yavl. raspad vozbuzhdennyh sostoyanii 126C6 i 168O8 (ris. 6). Vozbuzhdenie etih U.e. v solnechnyh vspyshkah osushestvlyaetsya energichnymi protonami. Drugim primerom vozbuzhdeniya i deaktivacii yadernyh U.e. yavl. reakciya neitronnogo zahvata 11H1(n, $\gamma$)21H1, proishodyashaya pri stolknovenii neitrona i protona. Pri etom obrazuetsya Ya leiteriya ne v osnovnom, a v kvazisvyazannom sostoyanii na virtual'nom U.e., k-ryi raspolozhen v nepreryvnom spektre vblizi granicy dissociacii Ya (na 0,067 MeV vyshe ee). Pomsleduyushaya izluchatel'naya deaktivaciya etogo urovnya privodit k obrazovaniyu stabil'nogo Ya deiteriya, a izluchennyi $\gamma$-foton imeet energiyu 2,22 MeV. Gamma-fotony s takoi energiei takzhe nablyudayutsya v solnechnyh vspyshkah. Otmechennaya reakciya neitronnogo zahvata igraet bol'shuyu rol' v pervichnom kosmologich. nukleosinteze, t.k. s nee nachinaetsya cep' termoyadernyh reakcii, privodyashih k obrazovaniyu Ya geliya.

Lit.:
Bor O., Mottel'son B., Struktura atomnogo yadra, per. s angl., t. 1-2, M., 1971-77; Born M., Atomnaya fizika, per. s angl., 3 izd., M., 1970; El'yashevich M.A., Atomnaya i molekulyarnaya spektroskopiya, M., 1962; Muhin K.N., Eksperimental'naya yadernaya fizika, 3 izd., t. 1-2, M., 1974; Sobel'man I.I., Vvedenie v teoriyu atomnyh spektrov, M., 1977; Tatevskii V.M., Stroenie molekul, M., 1977.

(V.K. Hersonskii)


Glossarii Astronet.ru

L | R | A | B | V | G | D | E | Zh | Z | I | ' | K | L | M | N | O | P | R | S | T | U | F | H | C | Ch | Sh | Sh | E | Yu | Ya 
Publikacii s klyuchevymi slovami: urovni energii - Spektr lineichatyi
Publikacii so slovami: urovni energii - Spektr lineichatyi 		Karta smyslovyh svyazei dlya termina UROVNI ENERGII
Sm. takzhe:

Mneniya chitatelei [2]
Ocenka: 2.9 [golosov: 183]
 
O reitinge
Versiya dlya pechati Raspechatat'
Astronet | Nauchnaya set' | GAISh MGU | Poisk po MGU | O proekte | Avtoram

Kommentarii, voprosy? Pishite: info@astronet.ru ili syuda

Rambler's Top100 Yandeks citirovaniya