Rambler's Top100Astronet    
  po tekstam   po klyuchevym slovam   v glossarii   po saitam   perevod   po katalogu 		 

Zeemana effekt

 - rassheplenie spektral'nyh linii pod deistviem na izluchayushee veshestvo vnesh. magn. polya. 3. e., nablyudaemyi v spektrah poglosheniya, poluchil nazvanie obratnogo, vse ego zakonomernosti analogichny zakonomernostyam pryamogo 3. e. (nablyudaemogo v liniyah izlucheniya). 3. e. byl otkryt niderlandskim fizikom P. Zeemanom v 1896 g. pri laboratornyh issledovaniyah svecheniya parov natriya.
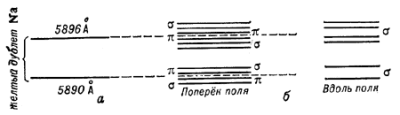
Ris. 1. Kartina rasshepleniya dvuh blizkih
spektral'nyh linii atoma natriya (zheltogo
dubleta Na) v magnitnom pole pri nablyudenii
poperek i vdol' polya; $\pi$- i $\sigma$-komponenty
polyarizovany razlichno.
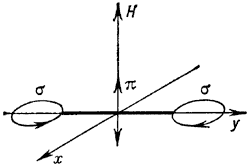
Ris. 1 illyustriruet zeemanovskoe rassheplenie dvuh blizkih spektr. linii atoma natriya, raspolozhennyh v zheltoi oblasti vidimogo spektra (t.n. zheltogo dubleta 5890 \AA i 5896 \AA). Kartina rasshepleniya sushestvenno zavisit ot napravleniya nablyudeniya po otnosheniyu k napravleniyu magn. polya. V svyazi s etim razlichayut prodol'nyi i poperechnyi 3. e. Pri nablyudenii perpendikulyarno magn. polyu (poperechnyi 3. e.) vse komponenty spektr. linii polyarizovany lineino (sm. Polyarizaciya elektromagnitnyh voln), chast' - parallel'no polyu H ($\pi$-komponenty), chast' - perpendikulyarno ($\sigma$-komponenty).
Ris. 2. Polyarizaciya $\pi$-komponentov
(poperechnyi effekt Zeemana) i
$\sigma$-komponentov (prodol'nyi effekt); H
- napravlenie magnitnogo polya, ploskost'
x, y - ploskost' polyarizacii
$\sigma$-komponentov.
Pri nablyudenii vdol' polya (prodol'nyi 3. e.) ostayutsya vidimymi lish' $\sigma$-komponenty, odnako lineinaya polyarizaciya ih smenyaetsya krugovoi (ris. 2). Raspredelenie intensivnosti v nablyudaemoi sisteme komponentov okazyvaetsya slozhnym.

Pervoe ob'yasnenie 3. e. bylo dano niderl. fizikom H. Lorencem v 1897 g. v ramkah klassich. teorii, soglasno k-roi dvizhenie elektrona v atome rassmatrivaetsya kak garmoniya, kolebaniya lineinogo oscillyatora. Po etoi teorii spektr. liniya pri poperechnom 3. e. rassheplyaetsya na tri komponenta. Takoe yavlenie poluchilo nazvanie normal'nogo 3. e., a rassheplenie linii na bol'shee chislo komponentov - anomal'nogo Z.e. Odnako obychno nablyudaetsya imenno anomal'nyi effekt. Isklyuchenie sostavlyayut perehody mezhdu singletnymi urovnyami, a takzhe sluchai sil'nogo magn. polya (sm. nizhe).

Polnoe ob'yasnenie 3. e. poluchil na osnove kvantovoi teorii. Urovni energii atoma rassheplyayutsya v magn. pole na podurovni. Kvantovye perehody mezhdu podurovnyami dvuh urovnei porozhdayut komponenty spektr. linii. Kazhdyi energetich. uroven' atoma harakterizuetsya mehanich. momentom kolichestva dvizheniya J. Rassheplenie urovnei obuslovleno tem, chto s mehanich. momentom svyazan magn. moment
$\mu=-\mu_B g$J, $\mu_B=e\hbar/2mc$ , (1)
gde e, m - zaryad i massa elektrona, ($\mu$ - magneton Bora, a g - t.n. faktor Lande. Smysl razdeleniya koeff. na dva mnozhitelya poyasnyaetsya nizhe. Znak minus obuslovlen otricat. zaryadom elektrona. Vzaimodeistvie magnitnogo momenta $\mu$ s polem H izmenyaet energiyu urovnya. Velichina etogo vzaimodeistviya zavisit ot vzaimnoi orientacii $\mu$ i H. Vektor J v magn. pole mozhet imet' 2J+1 orientacii, pri k-ryh ego proekciya JH=M, gde M - magnitnoe kvantovoe chislo. Ono prinimaet znacheniya 0, $\pm 1,..., \pm J$. Stol'ko zhe znachenii mozhet imet' proekciya $\mu_H$ magn. momenta $\mu$ na napravlenie H. Poetomu uroven' rassheplyaetsya na 2J+1 komponentov. Izmenenie energii $\delta\varepsilon$ kazhdogo komponenta (po otnosheniyu k energii urovnya v otsutstvie polya) s uchetom f-ly (1) ravno:
$\delta\varepsilon=-\mu_H H=\mu_B g M H$. (2)
Mehanich. moment atoma skladyvaetsya iz orbital'nogo momenta L i spinovogo momenta S: J=L+S. Analogichno magn. moment $\mu=\mu_L+\mu_S$. Velichina $\mu_L$ podobna magn. momentu toka, obrazovannogo orbital'nym dvizheniem elektronov v atome, i ravna $-\mu_B$L. S velichinoi $\mu_S$ delo obstoit slozhnee, t.k. spinovyi moment S svyazan s vnutr. harakteristikoi elektronov, a ne s ih dvizheniem. Kak sleduet iz eksperimenta (a takzhe iz relyativistskoi kvantovoi teorii Diraka), $\mu_S=-2\mu_B$S, t.e. na edinicu spinovogo momenta prihoditsya vdvoe bol'shii magn. moment. T.o., polnyi magn. moment
$\mu=-\mu_B$(L+2S)=$-\mu_B$(J+S). (3)
Vektor $\mu$ precessiruet vokrug vektora J, tak chto v srednem on napravlen vdol' J, a ego velichina opredelyaetsya po f-le (1). Soglasno raschetam na osnove kvantovoi mehaniki, faktor Lande
g=1+[J(J+1)-L(L+1)+S(S+1)]/2J(J+1). (4)
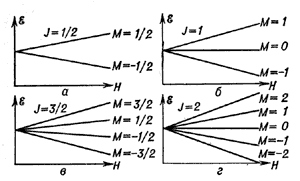
Ris. 3. Zavisimost' rasshepleniya urovnei
energii ot napryazhennosti magnitnogo polya:
a - pri J=1/2, b - pri J= 1, v - pri J=3/2,
g - pri J= 2, M - magnitnoe kvantovoe chislo.
Na ris. 3 pokazany primery zeemanovskogo rasshepleniya nek-ryh urovnei. V sootvetstvii s f-loi (2) smeshenie chastot komponentov linii ravno:
$\delta\nu={\mu_B H\over {h}}\;[g_2M_2-g_1M_1]$ . (5)
Izmenenie kvantovogo chisla M opredelyaetsya pravilom otbora $\Delta M=M_2-M_1=0,\pm 1$. Vsevozmozhnye perehody, udovletvoryayushie etomu pravilu, dayut zeemanovskuyu strukturu linii. V obshem sluchae znacheniya faktora Lande razlichny dlya verhnego i nizhnego urovnei, perehod mezhdu k-rymi obrazuet spektr. liniyu. T.o., perehody s razlichnymi M1 dayut raznye $\delta\nu$ dazhe pri odinakovom $\Delta M$. V rezul'tate poluchaetsya slozhnaya kartina - anomal'nyi 3. e. Esli u verhnego i nizhnego urovnei S=0, to J=L, g= 1, $\delta\nu=\mu_B H\Delta M/h$, t.e. okazyvayutsya vozmozhnymi vsego tri raznyh $\delta\nu$ (tri linii). Perehody mezhdu urovnyami s $\Delta M$= 0 dayut central'nyi $\pi$-komponent, a s $\Delta M=\pm 1$ - smeshennye $\sigma$-komponenty. Voznikaet norm. 3. e. (ris. 4). Shodnaya kartina poluchaetsya v chastnom sluchae, kogda g1=g2.

V ochen' sil'nom pole H svyaz' L i S narushaetsya, oba vektora nachinayut nezavisimo drug ot druga precessirovat' vokrug napravleniya J s proekciyami ML i MS. Narushenie svyazi imeet mesto v sluchae, kogda zeemanovskoe rassheplenie stanovitsya bol'she tonkoi struktury, t.e. J-struktury urovnya LS. Pri etom $\mu_H=(M_L+2M_S)\mu_B$. Pravilo otbora dlya $\Delta M_L$ takoe zhe, kak dlya $\Delta M$, a $\Delta M_S$= 0. Poetomu $\delta\nu=\mu_B H\Delta M_L/h$ i opyat' proyavlyaetsya norm. 3. e. V dannyh usloviyah kazhdyi zeemanovskii komponent imeet tonkuyu strukturu (podobno J-strukture urovnya LS). Komponenty etoi struktury harakterizuyutsya znacheniem velichiny $M_L\cdot M_S$. Perehod ot anomal'nogo k normal'nomu 3. e. v sil'nom pole naz. effektom Pashena-Baka. Pri perehode narushaetsya lineinaya zavisimost' smesheniya ot polya. Dlya razlichnyh linii effekt voznikaet pri raznyh velichinah magn. polya.

V astrofizike 3. e. ispol'zuetsya dlya opredeleniya magn. polei kosmich. ob'ektov.
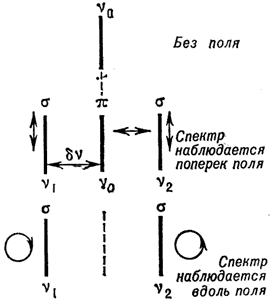
Ris. 4. Normal'nyi effekt Zeemana;
strelkami oboznachena polyarizaciya
komponentov, $\nu_0$ - chastota ishodnoi
linii, $\nu_1=\nu_0-\delta\nu$ i $\nu_2=\nu_0+\delta\nu$ -
chastoty $\sigma$-komponentov.

Pri izmereniyah magn. polei zvezd zeemanovskoe rassheplenie spektr. linii obychno nablyudaetsya v pogloshenii. Prodol'nyi komponent magn. polya izmeren u nesk. soten zvezd razlichnyh spektral'nyh klassov. Vyyasneno, chto indukciya magn. polya na poverhnosti t.n. magnitnyh zvezd dostigaet nesk. tysyach Gs, a u zvezdy HD 215441 nablyudaetsya sil'noe pole $\approx 3,4\cdot 10^4$ Gs. Ochen' sil'nye magn. polya, prevoshodyashie 10 Gs, obnaruzheny po 3. e. u neskol'kih vyrozhdennyh zvezd - belyh karlikov.

Magn. polya Galaktiki mozhno izmerit' po zeemanovskomu rasshepleniyu radiolinii vodoroda 21 sm. Vybor linii poglosheniya dlya takih izmerenii pozvolyaet nablyudat' na fone yarkogo radioistochnika rezkuyu liniyu i znachitel'no umen'shit' rol' shumov i vozmozhnyh oshibok. Takim metodom byli izmereny magn. polya v plotnyh i holodnyh oblakah mezhzvezdnogo gaza, proeciruyushihsya na yarkie galaktich. radioistochniki: Kassiopeya A, Telec A i dr. Okazalos', chto v oblake, raspolozhennom v napravlenii istochnika Kassiopeya A, magn. pole dostigaet $(18\pm 2)\cdot 10^{-6}$ Gs. Srednee krupnomasshtabnoe pole Galaktiki imeet velichinu $\approx 2\cdot 10^{-6}$ Gs, a v oblakah gaza magn. pole v 5-10 raz bol'she. Takim putem opredelyaetsya tol'ko prodol'nyi (vdol' lucha zreniya) komponent magn. polya.

Izuchenie magn. polei aktivnyh oblastei, pyaten i dr. obrazovanii na Solnce proizvoditsya s pomosh'yu osobyh chuvstvitel'nyh priborov - fotoelektrich. magnitografov, pozvolyayushih izmeryat' polya do 1 Gs i men'she (sostavlyayushuyu polya po luchu zreniya). Pri takih izmereniyah takzhe ispol'zuetsya obratnyi 3. e. V bol'shinstve sluchaev zeemanovskie komponenty linii slivayutsya mezhdu soboi - nalichie magn. polya vyzyvaet obshee rasshirenie spektr. linii. Magn. pole opredelyaetsya v etih sluchayah polyarizac. metodami. Pri nablyudeniyah anomal'nogo 3. e., kogda liniya rassheplyaetsya na ryad $\pi$- i $\sigma$-komponentov, dlya opredeleniya velichiny rasshepleniya ($\delta\lambda_H$) $\sigma$-komponentov astrofiziki ispol'zuyut f-lu: $\delta\lambda_H\pm 4,67\cdot 10^{-13} g\lambda^2 H$, gde N vyrazheno v E, dlina volny $\lambda$ v \AA. Obychno dlya izmerenii solnechnyh magn. polei ispol'zuyut spektr. liniyu zheleza $\lambda= 5250,4$ \AA (FeI) s faktorom g= 3 i ryad dr. linii. Poskol'ku zeemanovskie komponenty linii polyarizovany razlichno (v prodol'nom 3. e. linii imeyut pravuyu i levuyu krugovuyu polyarizaciyu, v obshem sluchae - ellipticheskuyu), izmenenie znaka nablyudaemoi polyarizacii smeshaet liniyu. Velichina smesheniya, fiksiruemaya fotoelektrich. magnitografom, opredelyaet prodol'nuyu sostavlyayushuyu napryazhennosti polya. Dlya polucheniya informacii o velichine i napravlenii polnogo vektora magn. polya na Solnce neobhodimo izmerit' parametry polyarizacii v nek-rom uchastke spektr. linii i ispol'zovat' rezul'taty teorii obrazovaniya linii v magn. pole. Dlya etoi celi obychno prinimaetsya nek-raya model' atmosfery i predpolagaetsya odnorodnost' magn. polya v sloe obrazovaniya spektr. linii. Polnyi vektor indukcii magn. polya izmeryaetsya s gorazdo men'shei tochnost'yu (50-100 Gs). Obshee magn. pole Solnca kak zvezdy sostavlyaet v srednem ok. 1 Gs, odnako v solnechnyh pyatnah velichina polya znachitel'no vyshe i dostigaet nesk. tysyach Gs.

Osobyi interes predstavlyayut sverhsil'nye magn. polya ~ 106-109 Gs u poverhnosti nek-ryh belyh karlikov i ~ 1011-1013 Gs (a mozhet byt', i vyshe) u poverhnosti ryada neitronnyh zvezd. V sverhsil'nyh polyah razrushaetsya svyaz' orbital'nyh i spinovyh momentov (li i si), k-rye v otsutstvie polya obrazuyut momenty L i S: L=$\sum\limits_i {\bf l}_i$, S=$\sum\limits_i {\bf s}_i$. V rezul'tate imeet mesto 3. e. otdel'nyh kvazinezavisimyh elektronov. V ochen' sil'nyh polyah narushaetsya central'naya simmetriya atoma, i atom (ili ion) priobritaet formu veretena. Takaya situaciya imeet mesto na poverhnosti neitronnyh zvezd

(L.A. Vainshtein, V.M. Tomozov)


Glossarii Astronet.ru

L | R | A | B | V | G | D | E | Zh | Z | I | ' | K | L | M | N | O | P | R | S | T | U | F | H | C | Ch | Sh | Sh | E | Yu | Ya 
Publikacii s klyuchevymi slovami: effekt Zeemana - magnitnoe pole - spektral'nye linii - rassheplenie spektral'nyh linii
Publikacii so slovami: effekt Zeemana - magnitnoe pole - spektral'nye linii - rassheplenie spektral'nyh linii 		Karta smyslovyh svyazei dlya termina ZEEMANA EFFEKT
Sm. takzhe:
Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu
Ocenka: 3.2 [golosov: 89]
 
O reitinge
Versiya dlya pechati Raspechatat'
Astronet | Nauchnaya set' | GAISh MGU | Poisk po MGU | O proekte | Avtoram

Kommentarii, voprosy? Pishite: info@astronet.ru ili syuda

Rambler's Top100 Yandeks citirovaniya