- zavisimost' ekvivalentnoi shiriny 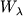 spektral'noi linii poglosheniya, ot chisla pogloshayushih atomov, formiruyushih
etu liniyu. Inogda ispol'zuyutsya K. r. dlya linii izlucheniya (esli raspredelenie atomov
po urovnyam energii sootvetstvuet raspredeleniyu Bol'cmana), opredelyayushie polnuyu intensivnost'
linii izlucheniya v zavisimosti ot chisla izluchayushih atomov. K. r. primenyayutsya dlya opredeleniya
him. sostava zvezdnyh i planetnyh atmosfer, obolochek novyh i sverhnovyh zvezd,
mezhzvezdnyh oblakov i dr. ob'ektov s lineichatym spektrom. S pomosh'yu K. r. nahodyat
takzhe temp-ru T i skorost' mikroturbulentnyh dvizhenii gaza vturb.
Analiz proizvoditsya putem sravneniya teoreticheskih i poluchennyh iz nablyudenii K. r.
spektral'noi linii poglosheniya, ot chisla pogloshayushih atomov, formiruyushih
etu liniyu. Inogda ispol'zuyutsya K. r. dlya linii izlucheniya (esli raspredelenie atomov
po urovnyam energii sootvetstvuet raspredeleniyu Bol'cmana), opredelyayushie polnuyu intensivnost'
linii izlucheniya v zavisimosti ot chisla izluchayushih atomov. K. r. primenyayutsya dlya opredeleniya
him. sostava zvezdnyh i planetnyh atmosfer, obolochek novyh i sverhnovyh zvezd,
mezhzvezdnyh oblakov i dr. ob'ektov s lineichatym spektrom. S pomosh'yu K. r. nahodyat
takzhe temp-ru T i skorost' mikroturbulentnyh dvizhenii gaza vturb.
Analiz proizvoditsya putem sravneniya teoreticheskih i poluchennyh iz nablyudenii K. r.
Liniya poglosheniya formiruetsya v verhnei chasti fotosfery
zvezdy, gde koeff. selektivnogo (v chastotah linii) poglosheniya zametno prevoshodit
koeff. nepreryvnogo poglosheniya. Profil' (chastotnaya zavisimost') koeff. poglosheniya
v predelah spektral'noi linii obychno yavl. svertkoi dvuh profilei: uzkogo gaussovogo
profilya,
polushirina k-rogo (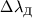 ) opredelyaetsya skorostyami teplovogo
i mikroturbulentnogo dvizhenii (t.n. doplerovskaya polushirina
) opredelyaetsya skorostyami teplovogo
i mikroturbulentnogo dvizhenii (t.n. doplerovskaya polushirina
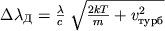
gde m - massa atoma), i shirokogo lorencevskogo profilya, polushirina k-rogo
GL obuslovlena radiacionnym i stolknovitel'nym zatuhaniem
izlucheniya
(sm. ris. 4 i 3 v st. Spektral'nye linii).
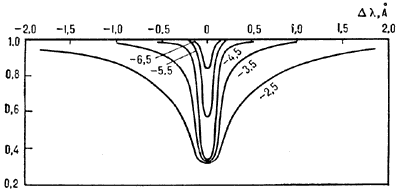
K. r. stroyat obychno v shkale 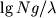 po osi absciss i
po osi absciss i 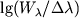 po osi ordinat, gde g - statistich. ves nizhnego
urovnya
dlya rassmatrivaemogo perehoda, N - chislo pogloshayushih atomov na luche zreniya
(v stolbike edinichnogo secheniya) v oblasti obrazovaniya linii, f - sila oscillyatora
linii. Bezrazmernaya velichina f predstavlyaet soboi effektivnoe chislo klassich.
oscillyatorov, kotorye po pogloshatel'nomu deistviyu v dannoi linii zamenyayut odin atom.
Dlya
rezonansnyh linii f ~ 1.
po osi ordinat, gde g - statistich. ves nizhnego
urovnya
dlya rassmatrivaemogo perehoda, N - chislo pogloshayushih atomov na luche zreniya
(v stolbike edinichnogo secheniya) v oblasti obrazovaniya linii, f - sila oscillyatora
linii. Bezrazmernaya velichina f predstavlyaet soboi effektivnoe chislo klassich.
oscillyatorov, kotorye po pogloshatel'nomu deistviyu v dannoi linii zamenyayut odin atom.
Dlya
rezonansnyh linii f ~ 1.
|
Ris. 1. Izmenenie teoreticheskogo profilya
linii Si II (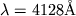 ) v spektre ) v spektre
zvezdy spektral'nogo klassa AO V s
izmeneniem obiliya kremniya
lg(NSi/NH) (cifry
u krivyh),
NSi, NH -
koncentracii atomov kremniya i vodoroda.
|
Kachestvenno hod K. r. vyglyadit sled. obr. Pri malom N liniya slaba i zavisimost'
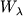 ot N prakticheski lineinaya (ris. 1, 2). Po mere uvelicheniya
N opticheskaya tolsha v centre linii,
gde koeff. poglosheniya maksimalen, stanovitsya bol'she edinicy i (vsledstvie eksponencial'nogo
haraktera poglosheniya) nastupaet nasyshenie central'noi chasti linii (central'naya glubina
linii poglosheniya perestaet rasti). Rost
ot N prakticheski lineinaya (ris. 1, 2). Po mere uvelicheniya
N opticheskaya tolsha v centre linii,
gde koeff. poglosheniya maksimalen, stanovitsya bol'she edinicy i (vsledstvie eksponencial'nogo
haraktera poglosheniya) nastupaet nasyshenie central'noi chasti linii (central'naya glubina
linii poglosheniya perestaet rasti). Rost 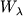 zamedlyaetsya i v dal'neishem
proishodit uzhe za schet bolee dalekih ot centra eshe ne nasyshennyh chastei linii (gde
koeff. poglosheniya ne slishkom mal), prichem
zamedlyaetsya i v dal'neishem
proishodit uzhe za schet bolee dalekih ot centra eshe ne nasyshennyh chastei linii (gde
koeff. poglosheniya ne slishkom mal), prichem 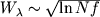 .
Pri dal'neishem
uvelichenii N eti chasti linii takzhe nasyshayutsya i rost proishodit za schet shirokih
nenasyshennyh lorencevskih kryl'ev linii, pri etom
.
Pri dal'neishem
uvelichenii N eti chasti linii takzhe nasyshayutsya i rost proishodit za schet shirokih
nenasyshennyh lorencevskih kryl'ev linii, pri etom 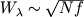 .
Pervaya chast' K. r. naz. lineinoi, vtoraya - pologoi ili perehodnoi, a tret'ya - oblast'yu
zatuhaniya izlucheniya. T.k. harakter nasysheniya v linii zavisit ot profilya koeff. poglosheniya,
forma K. r. zavisit ot parametrov
.
Pervaya chast' K. r. naz. lineinoi, vtoraya - pologoi ili perehodnoi, a tret'ya - oblast'yu
zatuhaniya izlucheniya. T.k. harakter nasysheniya v linii zavisit ot profilya koeff. poglosheniya,
forma K. r. zavisit ot parametrov 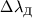 i GL.
i GL.
|
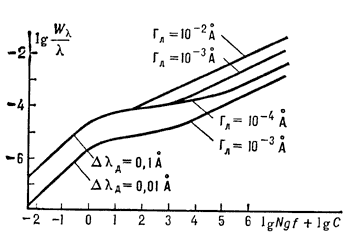
Ris. 2. Shematicheskie krivye rosta dlya
razlichnyh znachenii parametrov 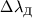 i GL.
i GL.
Velichina S ne zavisit ot N, g i f;
ee znachenie opredelyaetsya prinyatoi
model'yu formirovaniya linii i
fizicheskimi konstantami.
|
Dlya postroeniya K. r. po nablyudeniyam ispol'zuyutsya linii poglosheniya atomov ili ionov,
vhodyashie v mul'tiplety, t.e. imeyushie obshii nizhnii uroven' energii i razlichayushiesya
velichinoi
gf. Dlya linii odnogo mul'tipleta,
nachinayushegosya s i-go urovnya, chisla pogloshayushih atomov Ni
odinakovy. V usloviyah termodinamicheskogo
ravnovesiya chislo atomov na i-m urovne
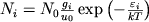 ili
ili
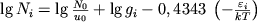
gde 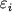 - potencial vozbuzhdeniya i-go urovnya, u0
- summa po sostoyaniyam (obychno
- potencial vozbuzhdeniya i-go urovnya, u0
- summa po sostoyaniyam (obychno 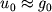 ),
N0 - chislo atomov na osn. urovne
),
N0 - chislo atomov na osn. urovne 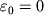 (sm. Bol'cmana raspredelenie).
Znacheniya gi i fi
izvestny zaranee, oni vychislyayutsya s pomosh'yu teorii atomnyh spektrov. Velichiny fi
mogut byt' takzhe polucheny putem laboratornyh izmerenii. Dlya kazhdoi linii odnogo mul'tipleta
opredelennoe po spektru znachenie
(sm. Bol'cmana raspredelenie).
Znacheniya gi i fi
izvestny zaranee, oni vychislyayutsya s pomosh'yu teorii atomnyh spektrov. Velichiny fi
mogut byt' takzhe polucheny putem laboratornyh izmerenii. Dlya kazhdoi linii odnogo mul'tipleta
opredelennoe po spektru znachenie 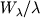 nanositsya na grafik
v zavisimosti ot
nanositsya na grafik
v zavisimosti ot 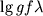 . T.o., po raznym mul'tipletam poluchayutsya
otrezki K. r., sdvinutye drug otnositel'no druga po osi absciss na rasstoyanie
. T.o., po raznym mul'tipletam poluchayutsya
otrezki K. r., sdvinutye drug otnositel'no druga po osi absciss na rasstoyanie 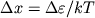 (ris. 3), gde
(ris. 3), gde 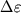 - raznost'
potencialov vozbuzhdeniya nizhnih urovnei mul'tipletov. Izmeriv eti rasstoyaniya, mozhno
opredelit'
temp-ru T teh sloev, gde obrazuyutsya linii. Sovmestiv vse otrezki K. r., postroennye
po mul'tipletam, v odnu krivuyu tak, chtoby razbros tochek byl minimal'nym, poluchayut
nablyudaemuyu K. r. Peremesheniem vdol' osi ordinat i osi absciss ee sovmeshayut s odnoi
iz teoretich. K. r. Neobhodimyi dlya sovmesheniya sdvig po osi ordinat pozvolyaet naiti
- raznost'
potencialov vozbuzhdeniya nizhnih urovnei mul'tipletov. Izmeriv eti rasstoyaniya, mozhno
opredelit'
temp-ru T teh sloev, gde obrazuyutsya linii. Sovmestiv vse otrezki K. r., postroennye
po mul'tipletam, v odnu krivuyu tak, chtoby razbros tochek byl minimal'nym, poluchayut
nablyudaemuyu K. r. Peremesheniem vdol' osi ordinat i osi absciss ee sovmeshayut s odnoi
iz teoretich. K. r. Neobhodimyi dlya sovmesheniya sdvig po osi ordinat pozvolyaet naiti
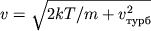 ,
a sdvig po osi absciss opredelyaet chislo pogloshayushih atomov Ni
(esli pri postroenii vse otrezki sdvigalis' k mul'tipletu s potencialom vozbuzhdeniya
nizhnego urovnya
,
a sdvig po osi absciss opredelyaet chislo pogloshayushih atomov Ni
(esli pri postroenii vse otrezki sdvigalis' k mul'tipletu s potencialom vozbuzhdeniya
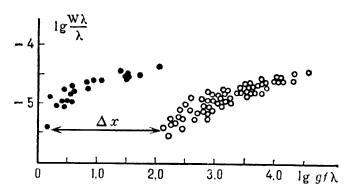
nizhnego urovnya 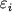 ). Opredeliv T i Ni
po f-le Bol'cmana vychislyayut N0. Postroiv
K. r. dlya vseh stadii ionizacii elementa i prosummirovav chisla atomov (ionov), na
etih stadiyah mozhno naiti polnoe chislo atomov dannogo elementa. Odnako, kak pravilo,
ne udaetsya
postroit' K. r. dlya vseh stadii ionizacii elementa, t.k. obychno v spektrah zvezd
odnovremenno nablyudayutsya linii ne bolee dvuh sosednih stadii ionizacii (napr., Fe
I i Fe II
ili Fe II i Fe III). Dlya opredeleniya chisla atomov elementa v nedostayushih stadiyah
ionizacii ispol'zuyut Saha formulu, v k-ruyu
v kachestve
neobhodimogo parametra krome temp-ry vhodit elektronnaya koncentraciya ne.
Etot parametr mozhet byt' naiden nezavisimo libo po nomeru poslednei
razlichimoi linii bal'merovskoi serii vodoroda (f-la Inglisa-Tellera), libo po chislu
ionov v dvuh stadiyah ionizacii (esli dlya etih stadii ionizacii mozhno postroit' K.
r. po
nablyudeniyam) i f-le Saha, polagaya T uzhe izvestnoi.
). Opredeliv T i Ni
po f-le Bol'cmana vychislyayut N0. Postroiv
K. r. dlya vseh stadii ionizacii elementa i prosummirovav chisla atomov (ionov), na
etih stadiyah mozhno naiti polnoe chislo atomov dannogo elementa. Odnako, kak pravilo,
ne udaetsya
postroit' K. r. dlya vseh stadii ionizacii elementa, t.k. obychno v spektrah zvezd
odnovremenno nablyudayutsya linii ne bolee dvuh sosednih stadii ionizacii (napr., Fe
I i Fe II
ili Fe II i Fe III). Dlya opredeleniya chisla atomov elementa v nedostayushih stadiyah
ionizacii ispol'zuyut Saha formulu, v k-ruyu
v kachestve
neobhodimogo parametra krome temp-ry vhodit elektronnaya koncentraciya ne.
Etot parametr mozhet byt' naiden nezavisimo libo po nomeru poslednei
razlichimoi linii bal'merovskoi serii vodoroda (f-la Inglisa-Tellera), libo po chislu
ionov v dvuh stadiyah ionizacii (esli dlya etih stadii ionizacii mozhno postroit' K.
r. po
nablyudeniyam) i f-le Saha, polagaya T uzhe izvestnoi.
|
Ris. 3. Uchastki krivyh rosta,
postroennye po liniyam mul'tipletov
Fe I s potencialami vozbuzhdeniya
0-1 eV (tochki) i 3-4 eV (kruzhki)
v spektre Prociona (spektral'nyi
klass F5 IV).
|
Teoreticheski K. r. mogut byt' rasschitany pri razlichnyh predpolozheniyah o processah
obrazovaniya linii poglosheniya. V modeli formirovaniya linii Shustera-Shvarcshil'da atmosfera
razdelena
na fotosferu, gde obrazuetsya tol'ko nepreryvnyi spektr, i obrashayushii sloi, gde obrazuyutsya
tol'ko linii poglosheniya (K. r. Unzol'da). Odnako v real'nyh atmosferah zvezd linii (za isklyucheniem samyh sil'nyh) obychno formiruyutsya
v usloviyah, kogda koeff. nepreryvnogo poglosheniya 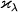 (v
raschete
na 1 g veshestva) ne yavl. ischezayushe malym po sravneniyu s koeff. selektivnogo poglosheniya
(v
raschete
na 1 g veshestva) ne yavl. ischezayushe malym po sravneniyu s koeff. selektivnogo poglosheniya
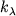 , i intensivnost' linii poglosheniya zavisit ot otnosheniya
, i intensivnost' linii poglosheniya zavisit ot otnosheniya 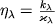 (model' Milna-Eddingtona, dlya k-roi K. r. byli rasschitany
Vrubelem). I te i dr. K. r. rasschitany v predpolozhenii nezavisimosti ot glubiny temp-ry
T, vturb i
(model' Milna-Eddingtona, dlya k-roi K. r. byli rasschitany
Vrubelem). I te i dr. K. r. rasschitany v predpolozhenii nezavisimosti ot glubiny temp-ry
T, vturb i 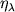 v sloe,
gde obrazuyutsya linii. K. r., vychislennye putem resheniya ur-niya perenosa izlucheniya
s ispol'zovaniem
chislennyh modelei atmosfer, uchityvayut izmenenie fiz. uslovii (temp-ry, plotnosti,
ionizacii) s glubinoi i dayut neposredstvenno zavisimost'
v sloe,
gde obrazuyutsya linii. K. r., vychislennye putem resheniya ur-niya perenosa izlucheniya
s ispol'zovaniem
chislennyh modelei atmosfer, uchityvayut izmenenie fiz. uslovii (temp-ry, plotnosti,
ionizacii) s glubinoi i dayut neposredstvenno zavisimost' 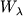 ot
obiliya
elementa. V metode modelei atmosfer dlya analiza him. sostava mogut byt' ispol'zovany
nablyudeniya malogo chisla linii ili dazhe tol'ko odnoi linii bez postroeniya K. r. po
nablyudeniyam,
esli parametry modeli atmosfery (effektivnaya
temperatura i uskorenie sily tyazhesti), a sledovatel'no, i teoretich. K. r. vybrany
na osnove nezavisimyh kriteriev (spektral'nogo
klassa, profilei vodorodnyh linii, raspredeleniya energii v nepreryvnom spektre).
Mnogochisl. issledovaniya pokazyvayut, chto dannye ob obilii him. elementov, poluchaemye
pri ispol'zovanii vseh treh vidov K. r., razlichayutsya ne sil'no. Osn. pogreshnost'
v rezul'taty
vnosyat pogreshnosti izmereniya
ot
obiliya
elementa. V metode modelei atmosfer dlya analiza him. sostava mogut byt' ispol'zovany
nablyudeniya malogo chisla linii ili dazhe tol'ko odnoi linii bez postroeniya K. r. po
nablyudeniyam,
esli parametry modeli atmosfery (effektivnaya
temperatura i uskorenie sily tyazhesti), a sledovatel'no, i teoretich. K. r. vybrany
na osnove nezavisimyh kriteriev (spektral'nogo
klassa, profilei vodorodnyh linii, raspredeleniya energii v nepreryvnom spektre).
Mnogochisl. issledovaniya pokazyvayut, chto dannye ob obilii him. elementov, poluchaemye
pri ispol'zovanii vseh treh vidov K. r., razlichayutsya ne sil'no. Osn. pogreshnost'
v rezul'taty
vnosyat pogreshnosti izmereniya 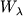 po nablyudaemym spektram i pogreshnosti
v ispol'zuemyh znacheniyah sil oscillyatorov f.
po nablyudaemym spektram i pogreshnosti
v ispol'zuemyh znacheniyah sil oscillyatorov f.
S pomosh'yu K. r. vypolneny obshirnye issledovaniya him. sostava zvezd nashei Galaktiki
i yarkih zvezd dr. galaktik, a takzhe issledovan harakter dvizhenii v atmosferah zvezd
razlichnogo
tipa. Udalos' vyyasnit', napr., chto mikroturbulentnaya skorost' dlya zvezd-karlikov
sostavlyaet 1-3 km/s, a dlya sverhgigantov ona v 10 raz bol'she; ustanovleno, chto obilie
zheleza
v zvezdah starogo naseleniya Galaktiki v 1000 raz
men'she, chem na Solnce.
Lit.:
Unzol'd A., Fizika zvezdnyh atmosfer, per. s nem., M., 1949; Mustel' E.R., Zvezdnye
atmosfery, M., 1960; Kauli Ch., Teoriya zvezdnyh spektrov, per. s angl., M., 1974.
(V.L. Hohlova)
![]() ) opredelyaetsya skorostyami teplovogo
i mikroturbulentnogo dvizhenii (t.n. doplerovskaya polushirina
) opredelyaetsya skorostyami teplovogo
i mikroturbulentnogo dvizhenii (t.n. doplerovskaya polushirina
![]()
![]() po osi absciss i
po osi absciss i ![]() po osi ordinat, gde g - statistich. ves nizhnego
urovnya
dlya rassmatrivaemogo perehoda, N - chislo pogloshayushih atomov na luche zreniya
(v stolbike edinichnogo secheniya) v oblasti obrazovaniya linii, f - sila oscillyatora
linii. Bezrazmernaya velichina f predstavlyaet soboi effektivnoe chislo klassich.
oscillyatorov, kotorye po pogloshatel'nomu deistviyu v dannoi linii zamenyayut odin atom.
Dlya
rezonansnyh linii f ~ 1.
po osi ordinat, gde g - statistich. ves nizhnego
urovnya
dlya rassmatrivaemogo perehoda, N - chislo pogloshayushih atomov na luche zreniya
(v stolbike edinichnogo secheniya) v oblasti obrazovaniya linii, f - sila oscillyatora
linii. Bezrazmernaya velichina f predstavlyaet soboi effektivnoe chislo klassich.
oscillyatorov, kotorye po pogloshatel'nomu deistviyu v dannoi linii zamenyayut odin atom.
Dlya
rezonansnyh linii f ~ 1.



