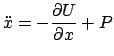Sovremennoe sostoyanie teorii dvizheniya iskusstvennyh sputnikov Zemli
T.V.Bordovicyna
Tomskii Gosudarstvennyi Universitet
Daetsya kratkoe opisanie sovremennogo sostoyaniya teorii dvizheniya iskusstvennyh sputnikov Zemli (ISZ). Rassmatrivayutsya analiticheskie i chislennye metody modelirovaniya dvizheniya ISZ. Sopostavlyayutsya vozmozhnosti sushestvuyushih teorii dvizheniya i potrebnostei ih prakticheskogo primeneniya.
|
Nastoyashaya lekciya yavlyaetsya svoeobraznym predstavleniem uchebnogo posobiya avtora na temu "Teoriya dvizheniya iskusstvennyh sputnikov Zemli. Analiticheskie i chislennye metody". Eta kniga napisana dlya togo, chtoby dat' studentam, specializiruyushimsya v oblasti nebesnoi mehaniki i kosmicheskoi geodezii, uchebnoe posobie, ohvatyvayushee esli ne vse, to hotya by bol'shinstvo metodov i podhodov, ispol'zuemyh dlya postroeniya analiticheskih i chislennyh modelei dvizheniya ISZ.
Za 45 let sushestvovaniya razdela nauki, imenuemogo dinamikoi ISZ, sozdano mnogo novyh metodov i algoritmov, prednaznachennyh kak dlya priblizhennogo, tak i dlya vysokotochnogo modelirovaniya dvizheniya, napisany podrobnye monografii i analiticheskie obzory, no uchebnikov prakticheski net. Vyshedshaya v 1965 g. kniga P. E. El'yasberga "Vvedenie v teoriyu poleta iskusstvennyh sputnikov Zemli", kotoruyu mozhno bylo by porekomendovat' studentam dlya pervonachal'nogo oznakomleniya s problemoi, davno stala bibliograficheskoi redkost'yu. A po sovremennym rezul'tatam net dazhe skol'ko-nibud' podrobnyh obzorov. Podgotovkoi nastoyashego posobiya my popytalis' likvidirovat' etot probel.
S matematicheskoi tochki zreniya zadacha o dvizhenii iskusstvennogo sputnika Zemli, kak i zadacha o dvizhenii lyubogo estestvennogo ob'ekta Solnechnoi sistemy, yavlyaetsya zadachei Koshi. Dvizhenie opisyvaetsya obyknovennymi differencial'nymi uravneniyami s nachal'nymi usloviyami.
Obychno dvizhenie iskusstvennogo sputnika Zemli predstavlyaetsya kak
dvizhenie material'noi chasticy beskonechno maloi massy v pole
tyagoteniya central'nogo tela s massoi 
pod deistviem sil,
opredelennyh potencial'noi funkciei 
, i sovokupnosti
nepotencial'nyh sil 
. V etom sluchae differencial'nye
uravneniya dvizheniya chasticy v pryamougol'noi inercial'noi sisteme
koordinat, svyazannoi s central'nym telom , mozhno zapisat'
sleduyushim obrazom:
s nachal'nymi usloviyami
 |
(2) |
gde
vektor polozheniya; 
fizicheskoe vremya; 
modul' vektora polozheniya;
, 
universal'naya
gravitacionnaya postoyannaya;
gradient; 
potencial vozmushayushih sil; 
sily, ne imeyushie
potenciala. Kolichestvo deistvuyushih na dvizhenie ISZ vozmushayushih sil
ves'ma veliko. K silam, imeyushim potencial, otnosyatsya vse sily
gravitacionnoi prirody. Eto vliyanie nesferichnosti Zemli,
vozmusheniya, svyazannye s prilivnymi deformaciyami Zemli, a takzhe
vliyanie Luny i Solnca. K silam, ne imeyushim potenciala, otnositsya
sila soprotivleniya atmosfery. Sila svetovogo davleniya na
iskusstvennyi sputnik Zemli dlya bol'shinstva ob'ektov yavlyaetsya
razryvnoi funkciei vremeni. Ee nepreryvnaya approksimaciya,
soderzhashaya funkciyu teni, takzhe yavlyaetsya nepotencial'noi, hotya sama
po sebe sila radiacionnogo davleniya imeet potencial.
Kak analiticheskii, tak i chislennyi podhody k resheniyu uravnenii nebesnoi mehaniki osnovany na priblizhenii reshenii otrezkami kakih-libo ryadov, odnako v postroenii etih reshenii est' principial'naya raznica.
Analiticheskii podhod pozvolyaet stroit' ryady, approksimiruyushie reshenie na znachitel'nyh intervalah vremeni ot odnogo do neskol'kih tysyach oborotov ob'ekta. Krome togo, ochen' sushestvenno, chto analiticheskaya approksimaciya hotya i mozhet zaviset' ot tipa orbity, no nikogda napryamuyu ne svyazana s nachal'nymi usloviyami uravnenii dvizheniya. V svyazi s etim analiticheskuyu approksimaciyu mozhno schitat' obshim resheniem. I imenno poetomu analiticheskie metody inogda nazyvayut metodami obshih vozmushenii.
Glavnaya trudnost' pri analiticheskom podhode sostoit v predstavlenii pravyh chastei uravnenii dvizheniya v vide yavnyh funkcii vremeni. Eto dostigaetsya putem razlozheniya vozmushayushei funkcii v ryad puassonovskogo tipa. Slozhnost' postroeniya tochnyh analiticheskih approksimacii resheniya uravnenii (1) privodit k tomu, chto bolee ili menee obshee reshenie, priemlemoe dlya razlichnyh tipov orbit, postroit' prakticheski nevozmozhno i primenenie kazhdoi otdel'noi teorii dvizheniya ogranicheno konkretnym klassom orbit.
Pri chislennom podhode k resheniyu uravnenii dvizheniya approksimaciya ishetsya v vide razlichnyh modifikacii otrezka ryada Teilora na intervale vremeni, sushestvenno men'shem odnogo oborota. Koefficienty razlozheniya, chto ochen' vazhno, vychislyayutsya, ishodya iz nachal'nyh uslovii uravnenii dvizheniya; i poluchennoe reshenie yavlyaetsya chastnym. Poetomu chislennye metody nazyvayut inogda metodami special'nyh ili chastnyh vozmushenii. V to zhe vremya sposob postroeniya chislennyh reshenii ochen' malo zavisit ot osobennostei rassmatrivaemoi orbity, i chislennye modeli dvizheniya stroyatsya obychno dlya vsego diapazona tipov orbit ISZ.
Pri chislennom podhode k resheniyu uravnenii (1) sushestvennymi stanovyatsya nekotorye obshie svoistva etih uravnenii. Tak, singulyarnost' uravnenii (1) v okrestnosti nachala koordinat dlya orbit, imeyushih bol'shie ekscentrisitety, privodit k sil'nym i neravnomernym izmeneniyam funkcii pravyh chastei uravnenii dvizheniya, chto pri primenenii chislennogo metoda trebuet postoyannogo izmeneniya shaga integrirovaniya i, kak sledstvie, vedet k neproizvoditel'nym zatratam komp'yuternogo vremeni. Krome togo, resheniya uravnenii (1) neustoichivy po Lyapunovu dazhe v nevozmushennom sluchae. Eta osobennost', sovershenno nesushestvennaya s tochki zreniya postroeniya analiticheskogo resheniya, v chislennom integrirovanii privodit k usileniyu oshibki usecheniya approksimiruyushei formuly metoda.
V doklade my rassmotrim oba podhoda k zadache modelirovaniya dvizheniya ISZ, obsudim specificheskie osobennosti kazhdogo podhoda i privedem prostye primery. Krome togo, my dadim obzor sovremennyh vysokotochnyh analiticheskih i chislennyh modelei dvizheniya ISZ i obsudim vozmozhnosti ih prakticheskogo primeneniya.
|
Publikacii s klyuchevymi slovami:
sputnik
Publikacii so slovami: sputnik | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |
