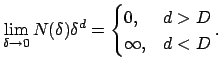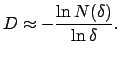<< Vvedenie Metody obnaruzheniya fraktal'nyh struktur >>
Fraktaly v matematike i fizike
Formal'noe opredelenie fraktal'nogo mnozhestva, predlozhennoe Benua
Mandel'brotom, vyglyadit sleduyushim obrazom:
Fraktal - mnozhestvo, razmernost' Hausdorfa-Bezikovicha kotorogo strogo
bol'she topologicheskoi.
Dlya opredeleniya ponyatiya razmernosti Hausdorfa-Bezikovicha (ona
zhe - "Hausdorfova razmernost'") vvedem neskol'ko oboznachenii.
Pust' est' mnozhestvo 
v prostranstve
.
Razob'em prostranstvo
na n-mernye kuby s dlinoi
rebra 
i oboznachim chislo kubov, neobhodimyh dlya pokrytiya
imi mnozhestva , cherez 
. Togda velichina razmernosti
Hausdorfa-Bezikovicha (nazyvaemoi takzhe fraktal'noi razmernost'yu)
dolzhna udovletvoryat' sleduyushemu usloviyu:
Dannoe opredelenie mozhno uprostit', sdelav ego bolee udobnym dlya
prakticheskogo primeneniya. Vidno, chto pri
iz (1) sleduet
Esli chislo
ne yavlyaetsya celym, to mnozhestvo - fraktal'no,
prichem ego fraktal'naya razmernost' ravna . Inogda o fraktal'noi
razmernosti govoryat i v tom sluchae, kogda mnozhestvo fraktal'nym ne
yavlyaetsya, v takom sluchae - celoe i sovpadaet s
topologicheskoi razmernost'yu mnozhestva.
Odnim iz osnovnyh priznakov fraktalov yavlyaetsya samopodobie.
Mnozhestvo nazyvaetsya samopodobnym, esli ono sovpadaet s
ob'edineniem 
neperesekayushihsya mnozhestv
,
kazhdoe iz kotoryh poluchaetsya iz szhatiem (izmeneniem vseh
masshtabov v 
raz, gde 
); velichina nazyvaetsya
koefficientom podobiya. Ochevidno, chto sushestvovanie hotya by odnogo
znacheniya dlya mnozhestva vlechet sushestvovanie
posledovatel'nosti 
s tochkoi sgusheniya
.
Dlya samopodobnyh mnozhestv vvoditsya ponyatie "razmernosti podobiya"
, opredelyaemoe iz
Sravnivaya (3) i (2), mozhno videt', chto dlya samopodobnogo mnozhestva (pri
fraktal'naya razmernost' i razmernost'
samopodobiya sovpadayut. Takie fraktaly (nazyvaemye samopodobnymi) obladayut
takzhe svoistvom skeilinga - masshtabnoi invariantnost'yu i invariantnost'yu
otnositel'no parallel'nogo perenosa (inogda v eto opredelenie vklyuchayut takzhe
trebovanie invariantnosti otnositel'no povorota).
Krome samopodobnyh fraktalov vydelyayutsya takzhe bolee slozhnye tipy fraktal'nyh mnozhestv. K nim mozhno otnesti samoafinnye fraktaly - s razlichnymi po razlichnym napravleniyam koefficientami podobiya (ili dazhe s otsutstviem podobiya v kakom-libo napravlenii), a takzhe mul'tifraktaly - s koefficientami podobiya, razlichnymi na razlichnyh prostranstvennyh masshtabah ili v razlichnyh oblastyah.
Pri opisanii fizicheskih ob'ektov neposredstvennoe ispol'zovanie ponyatiya mnozhestva daleko ne vsegda udobno. Chashe raspredelenie veshestva luchshe opisyvaetsya funkciei, zadayushei plotnost' veshestva v zavisimosti ot koordinat. Takie fraktal'nye funkcii, yavlyayushiesya v nekotorom smysle obobsheniyami ponyatiya fraktal'nogo mnozhestva, vpervye poyavilis' v XIX veke v rabotah nemeckogo matematika Karla Veiershtrassa, postroivshego pervyi primer nepreryvnoi funkcii, nigde ne imeyushei proizvodnoi.
Odnako vse vidy matematicheskih fraktalov yavlyayutsya abstrakciyami, neposredstvennoe primenenie kotoryh dlya opisaniya real'nyh fizicheskih ob'ektov vozmozhno tol'ko s nekotorymi ogovorkami. Matematicheskoe fraktal'noe mnozhestvo, kak eto sleduet iz ego opredeleniya, dolzhno obladat' nekotorymi "neestestvennymi" svoistvami. U nego dolzhny otsutstvovat' naibol'shii i naimen'shii masshtaby samopodobiya. Eto, v chastnosti, oznachaet, chto razmery minimal'nyh elementov mnozhestva stremyatsya k nulyu, v to vremya kak razmery vsego mnozhestva v celom dolzhny byt' beskonechno bol'shimi.
S drugoi storony, v lyuboi fizicheskoi strukture dolzhen sushestvovat' konechnyi naimen'shii masshtab. Krome togo, takaya struktura vsegda ogranichena v zanimaemom eyu prostranstve, chto privodit k narusheniyu samopodobiya vblizi granicy. Dostatochno malaya oblast', soderzhashaya granicu mnozhestva, ne podobna oblasti togo zhe razmera, nahodyasheisya vdali ot granicy. Poetomu lyubaya estestvennaya fraktal'naya struktura mozhet byt' lish' nekotorym priblizheniem k matematicheskomu fraktalu, prichem ee opisanie v ramkah fraktal'nyh mnozhestv mozhet byt' dostatochno korrektnym tol'ko pri rassmotrenii prostranstvennyh masshtabov, v dostatochnoi stepeni udalennyh kak ot minimal'nogo, tak i ot maksimal'nogo masshtabov sushestvovaniya struktury.
Poetomu Mandel'brotom bylo predlozheno drugoe opredelenie fraktala: Fraktalom nazyvaetsya struktura, sostoyashaya iz chastei, kotorye v kakom-to smysle podobny celomu. Eto opredelenie, dazhe pri ego nepolnote, vpolne sootvetstvuet osnovnomu svoistvu fraktalov - nablyudaemoi i poluchaemoi pri raschetah tozhdestvennosti struktury fraktala kak v celom, tak i dlya lyuboi ego oblasti.
Zametim, chto nikakaya fizicheskaya struktura ne mozhet, dazhe na dalekih ot granic fraktal'nosti masshtabah, absolyutno tochno vosproizvodit' matematicheskii fraktal, poskol'ku vsegda sushestvuyut razlichnye faktory, iskazhayushie strukturu. V kachestve takih faktorov mogut vystupat', naprimer, teplovye dvizheniya chastic, obrazuyushih strukturu, ili makroskopicheskie dvizheniya elementov struktury. Po etoi prichine fizicheskii fraktal obladaet tol'ko "statisticheskimi" fraktal'nymi svoistvami, v srednem sohranyaya fraktal'nuyu strukturu, no, vozmozhno, otklonyayas' ot nee v razlichnyh oblastyah v razlichnye momenty vremeni. Takie fpaktaly umestno nazyvat' "dinamicheskimi".
<< Vvedenie Metody obnaruzheniya fraktal'nyh struktur >>
