<< Fraktaly v matematike i Formirovanie struktur >>
Metody obnaruzheniya fraktal'nyh struktur
v astrofizicheskih ob'ektah
Dlya issledovaniya svoistv fraktal'noi struktury kakogo-libo fizicheskogo fraktala neobhodimo imet' kakoi-libo algoritm opredeleniya fraktal'noi razmernosti ob'ekta po dannym nablyudenii. Sushestvuet ves'ma bol'shoe kolichestvo razlichnyh metodov opredeleniya fraktal'noi razmernosti ili zamenyayushih ee velichin, odnako vse oni baziruyutsya na klassicheskom opredelenii fraktal'noi razmernosti, dannom Hausdorfom. Nekotorye iz etih algoritmov yavlyayutsya dostatochno prostymi i mogut byt' realizovany programmno; nekotorye predstavlyayut tol'ko matematicheskii interes, poskol'ku yavlyayutsya neprivodimymi i trebuyut beskonechnogo vremeni vychislenii. Ostanovimsya na nekotoryh metodah, primenenie kotoryh kak k astrofizicheskim ob'ektam predstavlyaetsya dostatochno opravdannym.
Odna iz vozmozhnyh harakteristik fraktal'noi struktury - korrelyacionnyi
pokazatel'. Pust' dlya ![]() tochek
tochek ![]() izuchaemogo mnozhestva
izuchaemogo mnozhestva ![]() v
prostranstve
v
prostranstve
![]() funkciya
funkciya
![]() - rasstoyanie mezhdu
tochkami. Vvedem funkciyu
- rasstoyanie mezhdu
tochkami. Vvedem funkciyu
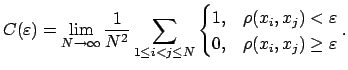 |
(4) |
Togda korrelyacionnym pokazatelem
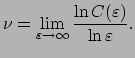 |
(5) |
Dlya samopodobnoi fraktal'noi struktury korrelyacionnyi pokazatel'
Tem ne menee v astrofizicheskih prilozheniyah chashe ispol'zuyutsya bolee prostye metody, osnovannye na podschetah kolichestva elementov struktury, soderzhashihsya v opredelennom ob'eme.
Pust' ob'ekt obladaet samopodobnoi fraktal'noi strukturoi, sostoit iz
odinakovyh elementov i v ob'emah, ogranichennyh koncentricheskimi sferami
radiusov ![]() i
i ![]() , soderzhit sootvetstvenno
, soderzhit sootvetstvenno ![]() i
i ![]() elementov.
Polagaem, chto
elementov.
Polagaem, chto
| (6) |
a velichina
gde
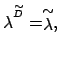 |
(8) |
opredelyayushee velichinu
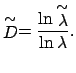 |
(9) |
Velichina
![]() dlya samopodobnyh fraktalov
sovpadaet s fraktal'noi razmernost'yu
dlya samopodobnyh fraktalov
sovpadaet s fraktal'noi razmernost'yu ![]() . Koefficient
. Koefficient ![]() ,
nazyvaemyi "prefaktorom", raven
,
nazyvaemyi "prefaktorom", raven
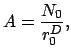 |
(10) |
gde
Vazhnoe dlya astrofizicheskih prilozhenii sootnoshenie sleduet iz (7) dlya
sistem, v kotoryh vse elementy imeyut odnu i tu zhe massu ![]() . Otnoshenie
mass, soderzhashihsya v sootvetstvuyushih sfericheskih ob'emah, zapisyvaetsya v
sleduyushem vide:
. Otnoshenie
mass, soderzhashihsya v sootvetstvuyushih sfericheskih ob'emah, zapisyvaetsya v
sleduyushem vide:
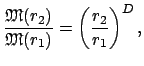 |
(11) |
otkuda, sledovatel'no,
Zdes' ![]() oznachaet rasstoyanie ot lyuboi proizvol'no vybrannoi tochki
struktury. Pri takom uslovii srednyaya plotnost' veshestva v
proizvol'nom sfericheskom ob'eme okazyvaetsya zavisyashei ot razmera
etogo ob'ema. Sushestvenno, chto eto utverzhdenie verno dlya vseh
tochek, vhodyashih v strukturu. Dlya real'nyh struktur znacheniya
oznachaet rasstoyanie ot lyuboi proizvol'no vybrannoi tochki
struktury. Pri takom uslovii srednyaya plotnost' veshestva v
proizvol'nom sfericheskom ob'eme okazyvaetsya zavisyashei ot razmera
etogo ob'ema. Sushestvenno, chto eto utverzhdenie verno dlya vseh
tochek, vhodyashih v strukturu. Dlya real'nyh struktur znacheniya ![]() v
razlichnyh tochkah struktury mogut poluchat'sya raznymi, chto
obuslovleno sluchainymi otkloneniyami struktury ot ideal'no
fraktal'noi, no esli poluchaemye "lokal'nye razmernosti" blizki
drug k drugu, to mozhno govorit' o sushestvovanii fraktal'noi
struktury s razmernost'yu, ravnoi srednemu znacheniyu lokal'nyh
razmernostei dlya vseh tochek struktury.
v
razlichnyh tochkah struktury mogut poluchat'sya raznymi, chto
obuslovleno sluchainymi otkloneniyami struktury ot ideal'no
fraktal'noi, no esli poluchaemye "lokal'nye razmernosti" blizki
drug k drugu, to mozhno govorit' o sushestvovanii fraktal'noi
struktury s razmernost'yu, ravnoi srednemu znacheniyu lokal'nyh
razmernostei dlya vseh tochek struktury.
Bolee slozhnoi yavlyaetsya sistema, sostoyashaya iz ob'ektov razlichnoi massy. Esli struktura sistemy fraktal'na, to v etom sluchae mnozhestvo, yavlyayusheesya geometricheskim "nositelem" ob'ektov, predstavlyaet soboi mul'tifraktal.
V nekotoryh sluchayah (naprimer, kogda zhelatel'no isklyuchit'
vozmozhnye effekty nablyudatel'noi selekcii) celesoobrazno
rassmatrivat' ne sfericheskie ob'emy, a tela odinakovoi, no
proizvol'noi formy, otlichayushiesya razmerom. V takom sluchae
vyrazhenie (12) takzhe ostaetsya istinnym, odnako ![]() priobretaet smysl harakternogo razmera, yavlyayushegosya parametrom
ispol'zuemyh ob'emov.
priobretaet smysl harakternogo razmera, yavlyayushegosya parametrom
ispol'zuemyh ob'emov.
K sozhaleniyu, v astrofizike chasto otsutstvuet polnaya informaciya o
prostranstvennoi strukture nablyudaemogo ob'ekta. V takom sluchae
fraktal'nuyu razmernost' prihoditsya opredelyat' po proekcii ob'ekta
na nebesnuyu sferu. Dlya mnogougol'nikov, krugov i drugih oblastei,
ogranichennyh obychnymi krivymi, otnoshenie dliny perimetra ![]() k
velichine
k
velichine ![]() , gde
, gde ![]() - ploshad' oblasti, yavlyaetsya
velichinoi, ne zavisyashei ot razmera oblasti. Odnako kogda oblast'
fraktal'na, to fraktalen i ee perimetr. Rezul'tat izmereniya
velichiny
- ploshad' oblasti, yavlyaetsya
velichinoi, ne zavisyashei ot razmera oblasti. Odnako kogda oblast'
fraktal'na, to fraktalen i ee perimetr. Rezul'tat izmereniya
velichiny ![]() v etom sluchae zavisit ot ispol'zuemogo etalona dliny.
Dlya fraktal'nogo perimetra
v etom sluchae zavisit ot ispol'zuemogo etalona dliny.
Dlya fraktal'nogo perimetra ![]() , zavisyashego ot velichiny
etalona
, zavisyashego ot velichiny
etalona ![]() ,
,
| (13) |
Ploshad' zhe oblasti, opredelyaemaya putem nalozheniya na nee kvadratov so storonoi
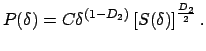 |
(14) |
Velichina
Poluchennaya velichina ![]() otnositsya k perimetru proekcii ob'ekta.
Odnako poskol'ku granica ob'ekta yavlyaetsya liniei peresecheniya
poverhnosti prostranstvennoi struktury s ploskost'yu, to znachenie
otnositsya k perimetru proekcii ob'ekta.
Odnako poskol'ku granica ob'ekta yavlyaetsya liniei peresecheniya
poverhnosti prostranstvennoi struktury s ploskost'yu, to znachenie
![]() dlya prostranstvennoi struktury mozhet byt' polucheno na
osnovanii tak nazyvaemoi "teoremy o slozhenii". Soglasno etoi
teoreme pri peresechenii samopodobnoi fraktal'noi struktury
razmernosti
dlya prostranstvennoi struktury mozhet byt' polucheno na
osnovanii tak nazyvaemoi "teoremy o slozhenii". Soglasno etoi
teoreme pri peresechenii samopodobnoi fraktal'noi struktury
razmernosti ![]() so strukturoi razmernosti
so strukturoi razmernosti ![]() v prostranstve
topologicheskoi razmernosti
v prostranstve
topologicheskoi razmernosti ![]() poluchaetsya struktura, obladayushaya
razmernost'yu
poluchaetsya struktura, obladayushaya
razmernost'yu ![]() , ravnoi
, ravnoi
| (15) |
otsyuda, v chastnosti, sleduet, chto fraktal'naya razmernost' prostranstvennoi struktury
<< Fraktaly v matematike i Formirovanie struktur >>