<< Interferenciya v optike. Opyt | Oglavlenie | Kalibrovka interferometra >>
Radiointerferometr
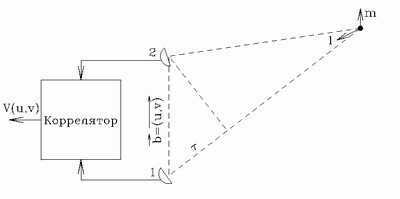
Rassmotrim sistemu iz dvuh radioteleskopov (ris. 3). V
otlichie ot optiki v radiodiapazone vozmozhna realizaciya
amplitudnogo detektora izlucheniya, to est' my mozhem registrirovat'
neposredstvenno 
, a ne
. Poetomu mozhno
svesti signal s obeih antenn na specializirovannyi komp'yuter,
nazyvaemyi korrelyatorom, gde budet vychislyat'sya korrelyaciya,
prisutstvuyushaya v vyrazhenii dlya intensivnosti. Takim obrazom, v
radiointerferometre neposredstvenno izmeryaetsya funkciya vidnosti
bez analiza interferencionnoi kartiny. Funkciyu vidnosti udobno
opredelit' sleduyushim obrazom:
.Eto opredelenie otlichaetsya ot vvedennogo ranee postoyannym mnozhitelem (
), funkciya vidnosti yavlyaetsya funkciei vektora
bazy (
na ris. 3), to est' vektora
rasstoyaniya mezhdu radioteleskopami 1 i 2. Kak i v sluchae s opytom
Yunga dlya protyazhennogo istochnika, raspredelenie yarkosti po
istochniku svyazano s funkciei vidnosti preobrazovaniem Fur'e
(formuly mogut byt' polucheny analogichno), odnako teper'
preobrazovanie Fur'e dvumerno, tak kak my v dannom sluchae ne
ogranichivaemsya sluchaem lineinogo istochnika.
.Vmesto odnoi prostranstvennoi chastoty
, ravnoi
rasstoyaniyu mezhdu shelyami v opyte Yunga, funkciya vidnosti zavisit
teper' ot dvuh prostranstvennyh chastot 
i 
, kotorye yavlyayutsya
proekciyami vektora bazy
na koordinatnye osi v
kartinnoi ploskosti. V etoi zhe sisteme koordinat s centrom v
istochnike issleduetsya i raspredelenie yarkosti 
, 
i
- napravlyayushie kosinusy. Udobno vybrat' dlya osi (i
sootvetstvenno ) napravlenie na vostok, a dlya osi (i
sootvetstvenno ) - na sever. Takim obrazom, smeshenie po
budet otvechat' smesheniyu po pryamomu voshozhdeniyu, a smeshenie po
- smesheniyu po skloneniyu. Obychno takzhe koordinaty i
bazy interferometra izmeryayut v edinicah dlin voln, togda uravnenie
(7) prinimaet klassicheskuyu formu preobrazovaniya Fur'e.
Chtoby poluchit' raspredelenie yarkosti po istochniku, neobhodimo
izmerit' funkciyu vidnosti dlya vseh znachenii i . Real'no eto
osushestvit' nel'zya, poetomu izmeryaemoe izobrazhenie budet iskazheno.
Esli vvesti funkciyu 
, kotoraya ravna 1 v teh tochkah
-ploskosti, dlya kotoryh byla izmerena funkciya vidnosti, a
inache - ravna 0, togda izmeryaemuyu funkciyu vidnosti
mozhno predstavit' v vide
.Funkciya
nazyvaetsya zapolneniem -ploskosti.
Po izvestnoi teoreme
o svertke preobrazovaniya Fur'e (sm., naprimer, [1]), poluchennoe
obrasheniem (7)
izobrazhenie budet svertkoi istinnogo izobrazheniya i
Fur'e-obraza , kotoryi nazyvaetsya "gryaznoi diagrammoi napravlennosti".
Sushestvuyut razlichnye metody vosstanovleniya izobrazheniya, odnako v lyubom
sluchae zhelatel'no poluchit' kak mozhno luchshee zapolnenie -ploskosti v
processe eksperimenta, chtoby oblegchit' rabotu etim metodam.
|
 |
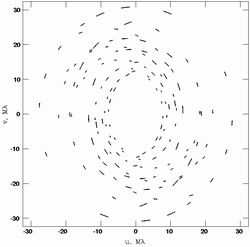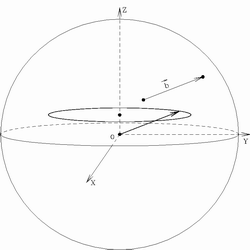
Ris. 4.
Zapolnenie -ploskosti. Na risunke sleva pokazano
formirovanie treka koncom vektora bazy za schet vrasheniya Zemli.
Sprava - primer real'nogo zapolneniya -ploskosti v
eksperimente s pyat'yu antennami. Poskol'ku istochnik nablyudalsya v
serii korotkih ekspozicii, dugi ellipsov ne sploshnye
Zapolnenie -ploskosti i sootvetstvenno izmerenie funkcii
vidnosti dlya razlichnyh i osushestvlyaetsya obychno za schet
vrasheniya Zemli. V koordinatah, svyazannyh s istochnikom, vektor bazy
vrashaetsya, tak chto ego konec opisyvaet v
prostranstve dugu okruzhnosti (ris. 4). V proekcii na
kartinnuyu ploskost' eto daet dugu ellipsa. Uvelichenie kolichestva
antenn v interferometre privodit, kak pravilo, k uvelicheniyu chisla
baz, chto takzhe uluchshaet zapolnenie -ploskosti. Na ris.4 sprava privedeno real'noe zapolnenie -ploskosti v
eksperimente s pyat'yu antennami. Koordinaty bazy i svyazany
sleduyushim obrazom s ee geocentricheskimi koordinatami
, gde os' 
napravlena v ploskosti ekvatora v napravlenii
meridiana (
), os' 
- na vostok (
), a os' 
- v napravlenii severnogo polyusa mira
(
):
,gde
i 
- chasovoi ugol i sklonenie istochnika sootvetstvenno.
Iz formuly (9) sleduet vazhnoe sledstvie: dlya okoloekvatorial'nyh
istochnikov bazy Zapad-Vostok (
) ne chuvstvitel'ny k skloneniyu
istochnika. Inymi slovami, na -ploskosti ellips vyrozhdaetsya v pryamuyu
liniyu 
. Esli vse bazy interferometra raspolozheny v napravlenii
Zapad-Vostok, to sintezirovannaya diagramma napravlennosti
(obratnoe Fur'e-preobrazovanie ot zapolneniya -ploskosti) imeet
beskonechnuyu shirinu po osi sklonenii dlya ekvatorial'nyh istochnikov.
<< Interferenciya v optike. Opyt | Oglavlenie | Kalibrovka interferometra >>
|
Publikacii s klyuchevymi slovami:
Radiointerferometr
Publikacii so slovami: Radiointerferometr | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |
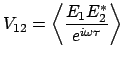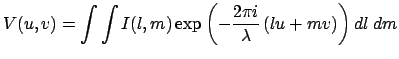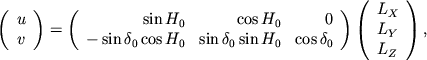